An object is attached to the bottom of a light verticle spring and set vibrating The maximum speed of the object is 15cm/sec and the time in centimeters is
3.0
2.0
1.5
1.0
The correct Answer is:C
To solve the problem, we need to find the amplitude of the oscillation of the object attached to the spring, given the maximum speed (v_max) and the time period (T). The maximum speed in simple harmonic motion is related to the amplitude and the time period by the formula:
vmax=A⋅ω
where ω is the angular frequency given by:
ω=2πT
Thus, we can rewrite the formula for maximum speed as:
vmax=A⋅2πT
From this equation, we can solve for the amplitude A:
A=vmax⋅T2π
1. Identify the given values:
- Maximum speed vmax=15cm/s (convert to meters: 15cm/s=0.15m/s)
- Time period T (not given, but we will express the amplitude in terms of T)
2. Substitute the values into the amplitude formula:
A=0.15⋅T2π
3. Calculate the amplitude:
- Since we do not have a specific value for T, we leave the amplitude in terms of T:
A=0.15⋅T2π
4. Final expression:
- The amplitude A is expressed as:
A=0.15T2πmeters
- Maximum speed vmax=15cm/s (convert to meters: 15cm/s=0.15m/s)
- Time period T (not given, but we will express the amplitude in terms of T)
A=0.15⋅T2π
- Since we do not have a specific value for T, we leave the amplitude in terms of T:
A=0.15⋅T2π
- The amplitude A is expressed as:
A=0.15T2πmeters
Topper's Solved these Questions
- OSCILLATION AND SIMPLE HARMONIC MOTIONBOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Simple Pendulum And Different Cases Of Shm
25 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Superposition Of Shm And Compound Pendulum
19 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Velocity , Acceleration And Energy Of Simple Harmonic Motion
40 Videos
- NEWTONS LAWS OF MOTIONBOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Chapter Test
30 Videos
- PROPERTIES OF MATTERBOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Chapter Test
29 Videos
Similar Questions
An object is vibrating at 50 hertz. What is its time period?
View SolutionAn object is attached to a vertical springs and lowered slowly to its equilibrium position. This stretches the spring by a distance d. If the same object is attached to the same vertical spring, but permitted to fall freely, through what distance does it stretch the spring ?
View Solution
Knowledge Check
An object is attched to the bottom of a light vertical spring and set vibrating. The maximum speed of the object is 15cm/s and the period is 628 milli seconds. The amplitude of the motion in centimetres is
A3.0B2.0C1.5D1.0An object of mass m, oscillating on the end of a spring with spring constant k has amplitude A. its maximum speed is
AA√k/mBA2k/mCA√m/kDAm/kA load of mass M is attached to the bottom of a spring of mass 'M/3' and spring constant 'K'. If the system is set into oscillation, the time period of oscillation is
A2π3√10MKB4π√M3KC4π√MKD2π√M3K
An object is placed at the bottom of a tank filled with liquid of refractive index 1.6. If the actual depth of the tank is 10 cm, what will be the apparent depth of the object?
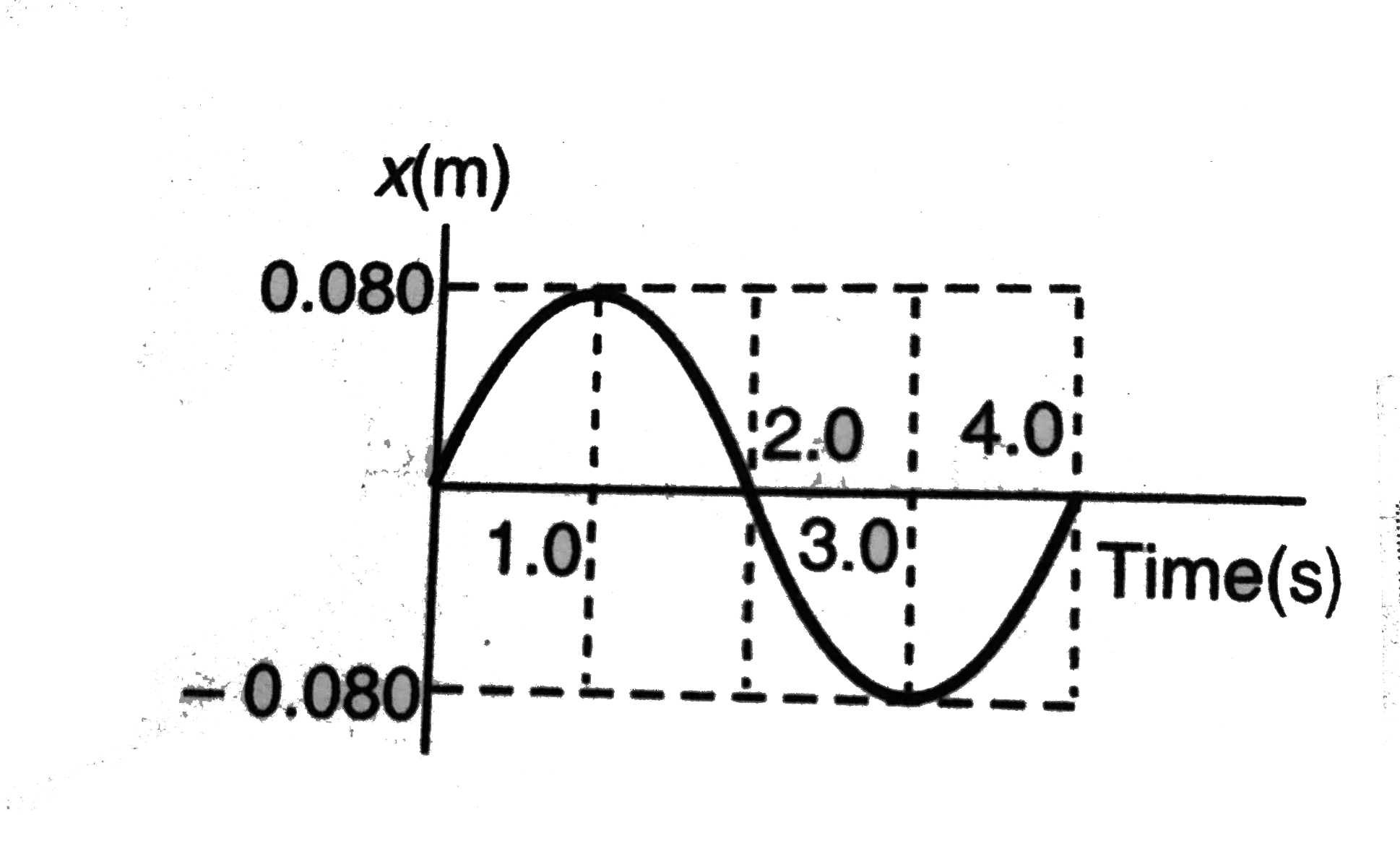
View SolutionAn object of mass 0.8kg is attached to one end of a spring and the system is set into simple harmonic motion. The displacement x of the object as a fuction of time is shown in the figure. With the aid of the data, determine
(a) the amplitude A of the motion,
(b) the angular frequency ω,
( c) the spring constant K,
(d) the speed of the object at t=1.0s and
(e) the magnitude of the object's acceleration at t=1.0s.
View SolutionA 0.20kg object mass attached to a spring whose spring constant is 500N/m executes simple harmonic motion. If its maximum speed is 5.0m/s, the amplitude of its oscillation is
View SolutionA mass of 1kg attached to the bottom of a spring has a certain frequency of vibration. The following mass has to be added to it in order to reduce the frequency by half :
View SolutionA mass of 1kg attached to the bottom of a spring has a certain frequency of vibration. The following mass has to be added to it in order to reduce the frequency by half :
View Solution