Consider a block symmetrically attached to two.identical massless springs by means of strings passing over light frictionless pulleys as shown in.the figure. In the equilibrium position extension in each spring is 0.5m. The time period of small vertical oscillation of the block is T second. Find the value of 5√3πT.
'(##CEN_KSR_PHY_JEE_C16_E01_027_Q11##)'
The correct Answer is:5
Topper's Solved these Questions
Similar Questions
Consider a block symmetrically attached to two identical massless springs by means of strings passing over light frictionless pulleys as shown. In the equilibrium position extension in the springs is x0. Find the time period of small vertically oscillations of the blocks.
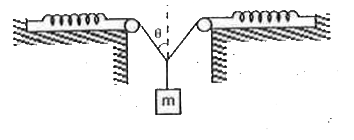
View SolutionConsider a block symmetrically attached to two identical massless springs by means of strings passing over light frictionless pulleys as shown. In the equilibrium position extension in the springs is x0. Find the time period of small vertically oscillations of the blocks.

View Solution
Knowledge Check
Two identical springs are attached to a small block P. The other ends of the springs are fixed at A and B, When P is in equilibrium the extension of bottom spring is 10 cm. The period of small vertical oscillations of P about is equilibrium position is (useg=9.8m/s2)
 A2π7secBπ7secC2π5secDnone of these
A2π7secBπ7secC2π5secDnone of theseTwo identical spring are attached to a small block P The other ends of the springs are fixed at A and B. when P is equilibrium the extension of top spring is 20cm and extension of bottom spring is 10cm The period at small vertical oscillation of p about its equilibrium position is (use g=9.8m/s2)
 A2π7secBπ7secC2π5secDnone of these
A2π7secBπ7secC2π5secDnone of these
The time period of small oscillations is kπ second. Find k.
Uniform square plate in vertical plane m=3kg k=12 N / m
'(##CEN_KSR_PHY_JEE_C16_E01_024_Q09##)'
View SolutionThe graph below shows a particle in simple harmonic motion. From the information shown, find the value of time t1(in S).
'(##CEN_KSR_PHY_JEE_C16_E01_010_Q03##)'
View SolutionTwo identical springs are attached to a small block P. The other ends of the springs are fixed at A and B, When P is in equilibrium the extension of bottom spring is 10 cm. The period of small vertical oscillations of P about is equilibrium position is (useg=9.8m/s2)

View SolutionIn the arrangement shown in the diagram, pulleys are small and springs are ideal. k1=k2=k3=k4=10Nm−1 are force constants of the springs and mass m=10kg. If the time period of small vertical oscillations of the block of mass m is given by 2πx seconds, then find the value of x.

View SolutionIn the arrangement shown in the diagram, pulleys are small and springs are ideal. k1=k2=k3=k4=10Nm−1 are force constants of the springs and mass m=10kg. If the time period of small vertical oscillations of the block of mass m is given by 2πx seconds, then find the value of x.

View SolutionA block of mass m is connected with two ideal pullies and a massless spring of spring constant K as shown in figure. The block is slightly displaced from its equilibrium position. If the time period of oscillation is μπ√mK. Then find the value of μ.

View Solution
