An electron starting from rest has a velocity that increase linearly with time that is v=kt,wher k=2 m//s^(@).Wˆwillbethedistancecovered∈first 3 seconds of its motion ?
To solve the problem of finding the distance covered by an electron whose velocity increases linearly with time, we can follow these steps:
Step 1: Understand the relationship between velocity and time
The velocity of the electron is given by the equation:
v=kt
where k=2m/s2. This indicates that the velocity increases linearly with time.
Step 2: Express the distance in terms of velocity
The distance x covered by the electron can be found by integrating the velocity function with respect to time. The relationship between distance, velocity, and time is given by:
x=∫vdt
Step 3: Set up the integral
Substituting the expression for velocity into the integral, we have:
x=∫t0ktdt
For our case, we want to find the distance covered in the first 3 seconds, so we set t=3 seconds:
x=∫30ktdt
Step 4: Perform the integration
Now, substituting k=2:
x=∫302tdt
Calculating the integral:
x=2∫30tdt
The integral of t is:
∫tdt=t22
Thus,
x=2(t22)30
x=2(322−022)
x=2(92−0)
x=2×92
x=9meters
Final Answer
The distance covered by the electron in the first 3 seconds of its motion is:
9meters
---
The velocity of the electron is given by the equation:
v=kt
where k=2m/s2. This indicates that the velocity increases linearly with time.
The distance x covered by the electron can be found by integrating the velocity function with respect to time. The relationship between distance, velocity, and time is given by:
x=∫vdt
Substituting the expression for velocity into the integral, we have:
x=∫t0ktdt
For our case, we want to find the distance covered in the first 3 seconds, so we set t=3 seconds:
x=∫30ktdt
Now, substituting k=2:
x=∫302tdt
Calculating the integral:
x=2∫30tdt
The integral of t is:
∫tdt=t22
Thus,
x=2(t22)30
x=2(322−022)
x=2(92−0)
x=2×92
x=9meters
The distance covered by the electron in the first 3 seconds of its motion is:
9meters
Topper's Solved these Questions
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 3 Short answer
37 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 4 Short answer
30 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 Short answer
25 Videos
- GRAVIATIONBOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - Assertion-Reason Type Questions
19 Videos
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Assertion- Reason Type Questions
17 Videos
Similar Questions
the velcoity -time relation of an electron starting from rest is given by v=kt,where h=2ms−2.calculate the distance traversed in 3s.
View SolutionA particle starting from rest moves in a straight line with acceleration as shown in the a-t graph. Find the distance (in m) travelled by the particle in the first four seconds from start of its motion.
Q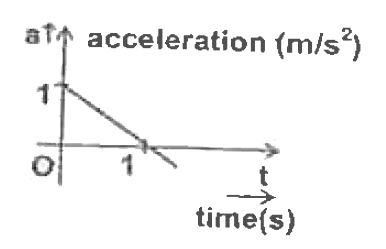
View Solution
Knowledge Check
A particle starts from rest and has velocity kt after time t. The distance travelled in time t is-
Akt2B2kt2Ck√tD1/2kt2A stone falls frecly from rest and the total distance covered by it in the last second of its motion cquals the distance covered by it in the first three seconds of its motion. The stone remains in the air for
A6sB5sC7sD4sAn object is given an initial velocity of 11m/s towards the north and a constant acceleration of 2m/s2 towards the south. What will be the distance covered by the object in the sixth second of its motion
A0.25mB0.5mC0D2m
The velocity-time relation of an electron starting from rest is given by u=id, where k=2m/s2. The distance traversed in 3 sec is:-
View SolutionA bus starts from rest and moves whith acceleration a=2ms2. The ratio of the distance covered in 6th second to that covered in 6 seconds is
View SolutionA body moving with uniform acceleration 8m/s2 starts from rest. The distance covered by it in fifth second will be
View SolutionA point initially at rest moves along x-axis. Its acceleration varies with time as a=(6t+5)m/s2. If it starts from origin, the distance covered in 2 s is:
View SolutionA particle is moving on a straight line. Its velocity at time t is (8−2t)m/s. What is the total distance covered from t=0 to t=6s?
View Solution
