The distance traversed by a moving particle at any instant is half of the product of its velocity and the time of travers. Show that the acceleration of particle is constant.
To show that the acceleration of a particle is constant given that the distance traversed by the particle at any instant is half of the product of its velocity and the time of travel, we can follow these steps:
Step 1: Write the given equation for distance
We start with the given equation for the distance s:
s=12vt
where s is the distance traveled, v is the velocity, and t is the time of travel.
Step 2: Differentiate the distance with respect to time
To analyze the relationship between distance, velocity, and acceleration, we differentiate s with respect to time t:
dsdt=12(v+tdvdt)
Here, we used the product rule of differentiation. The first term v is differentiated with respect to t, and the second term tdvdt is derived from the product of t and v.
Step 3: Relate velocity to acceleration
From the definition of acceleration a:
a=dvdt
We can substitute this into our differentiated equation. Thus, we have:
dsdt=12(v+ta)
Step 4: Set the expression for velocity
Since dsdt is also equal to the velocity v, we can set the two expressions equal:
v=12(v+ta)
Step 5: Simplify the equation
Multiplying both sides by 2 to eliminate the fraction gives:
2v=v+ta
Now, subtract v from both sides:
v=ta
Step 6: Solve for acceleration
From the equation v=ta, we can express acceleration as:
a=vt
This shows that acceleration is constant if v is constant over time t.
Step 7: Conclusion
Since we derived that a=vt and if v does not change with respect to time, then a must also be constant. Thus, we conclude that the acceleration of the particle is constant.
We start with the given equation for the distance s:
s=12vt
where s is the distance traveled, v is the velocity, and t is the time of travel.
To analyze the relationship between distance, velocity, and acceleration, we differentiate s with respect to time t:
dsdt=12(v+tdvdt)
Here, we used the product rule of differentiation. The first term v is differentiated with respect to t, and the second term tdvdt is derived from the product of t and v.
From the definition of acceleration a:
a=dvdt
We can substitute this into our differentiated equation. Thus, we have:
dsdt=12(v+ta)
Since dsdt is also equal to the velocity v, we can set the two expressions equal:
v=12(v+ta)
Multiplying both sides by 2 to eliminate the fraction gives:
2v=v+ta
Now, subtract v from both sides:
v=ta
From the equation v=ta, we can express acceleration as:
a=vt
This shows that acceleration is constant if v is constant over time t.
Since we derived that a=vt and if v does not change with respect to time, then a must also be constant. Thus, we conclude that the acceleration of the particle is constant.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 3 Short answer37videos
KINEMATICS
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 4 Short answer30videos
KINEMATICS
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 Short answer25videos
KINEMATICS
- BOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - Assertion-Reason Type Questions19videos
GRAVIATION
- BOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Assertion- Reason Type Questions17videos
LAWS OF MOTION
Similar Questions
A particle moves along a path y=ax2 (where a is constant) in such a way that x-component of its velocity (ux) remains constant. The acceleration of the particle is
View SolutionThe velocity of a particle at an instant "t" is v=u+at ,where u is initial velocity and a is constant acceleration.The v -t graph are
View Solution
Knowledge Check
- Question 1 - Select One
The coordinate of a moving particle at any instant of time t are x = at and y=bt2. The trajectory of the particle is
Ay=b2xa2By=b2x2a2Cy2=b2a2Dy=bx2a2 - Question 2 - Select One
The speed of a particle moving in a circle is increasing. The dot product of its acceleration and velocity is
AnegativeBzeroCpositiveDmay be positive or negative - Question 3 - Select One
A particle is moving on a straight line such that square of its velocity is directly proportional to distance as shown in graph. What is the acceleration of the particle ?
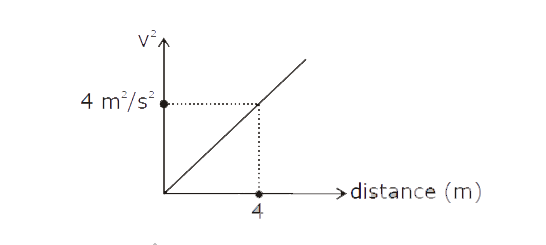 A14m/s2B1m/s2C2m/s2D12m/s2
A14m/s2B1m/s2C2m/s2D12m/s2
The coordinates of a particle moving in x-y plane at any time t are (2t,t2). Find (a) the trajectory of the particle, (b) velocity of particle at time t and (c) acceleration of particle at any time t.
View SolutionA graph between the square of the velocity of a particle and the distance s moved by the particle is shown in the figure. The acceleration of the particle is
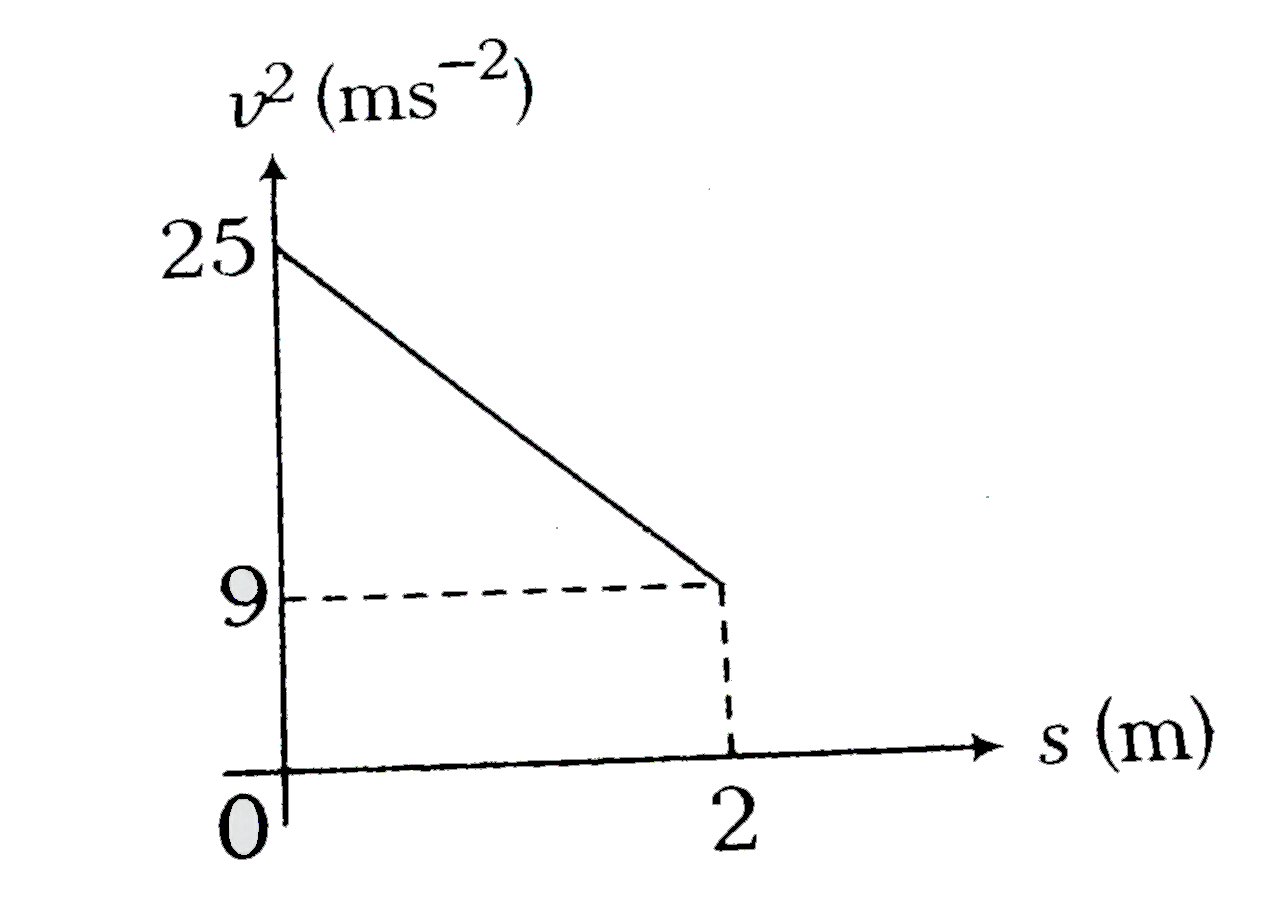 View Solution
View SolutionA particle is moving along X-axis Its acceleration at time t is proportional to its velocity at that time. The differential equation of the motion of the particle is
View SolutionA particle is moving on a circle of radius A .At an instant its speed and tangential acceleration are B and C respectively.Total acceleration of the particle at that instant is
View SolutionThe distance traversed by a particle moving along a straight lne is given by x=180t+50t2 metre. The acceleration of the particle is
View Solution

