A polytropic process for an ideal gas is represented by equation . If g is ratio of specific heats , then value of n for which molar heat capacity of the process is negative is given as
none, as it is not possible
The correct Answer is:B
is negative if .
Topper's Solved these Questions
- KINETIC THEORY OF GASES AND THERMODYNAMICSBOOK - A2ZCHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - Second Law Of Thermodynamics
29 Videos
- KINETIC THEORY OF GASES AND THERMODYNAMICSBOOK - A2ZCHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - Problems Based On Mixed Concepts
49 Videos
- KINETIC THEORY OF GASES AND THERMODYNAMICSBOOK - A2ZCHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - First Law Of Thermodynamics , Internal Energy And Work Done
55 Videos
- GRAVITATIONBOOK - A2ZCHAPTER - GRAVITATIONEXERCISE - Chapter Test
29 Videos
- MOCK TESTBOOK - A2ZCHAPTER - MOCK TESTEXERCISE - Motion With Constant Acceleration
15 Videos
Similar Questions
Find the value of molar heat capacity for an ideal gas in an adiabatic process.
View Solution(a) A polytropic process for an ideal gas is represented by PVx= constant, where x≠1. Show that molar specific heat capacity for such a process is given by C=Cv+R1−x.
(b) An amount Q of heat is added to a mono atomic ideal gas in a process in which the gas performs a work Q2 on its surrounding. Show that the process is polytropic and find the molar heat capacity of the gas in the process.
View Solution
Knowledge Check
For a reversible thermodynamic process for monoatomic gas PVx= constant If for this process x=CpCv, then heat capacity for the process is
A3R2B5R2C0D∞For an ideal monoatomic gas, molar heat capacity at constant volume (Cv) is
A23RB32RC52RD25RIf γ is the ratio of specific heats and R is the universal gas constant, then the molar specific heat at constant volume CV is given by
AγRB(γ−1)RγCRγ−1DγRγ−1
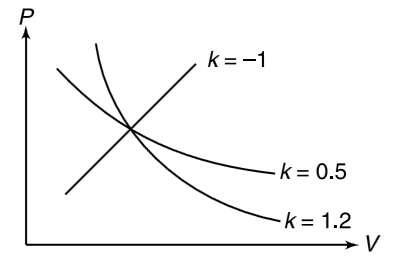
Figure shows P versus V graph for various processes performed by an ideal gas. All the processes are polytropic following the process equation PVk= constant.
(i) Find the value of k for which the molar specific heat of the gas for the process is CP+CV2. Does any of the graph given in figure represent this process?
(ii) Find the value of k for which the molar specific heat of the gas is CV+CP. Assume that gas is mono atomic. Draw approximately the P versus V graph for this process in the graph given above.
View SolutionAn ideal gas undergoes a process in which its pressure and volume are related as PVn=constant,where n is a constant.The molar heat capacity for the gas in this process will be zero if
View SolutionAn ideal has undergoes a polytropic given by equation PVn = constant. If molar heat capacity of gas during this process is arithmetic mean of its molar heat capacity at constant pressure and constant volume then value of n is
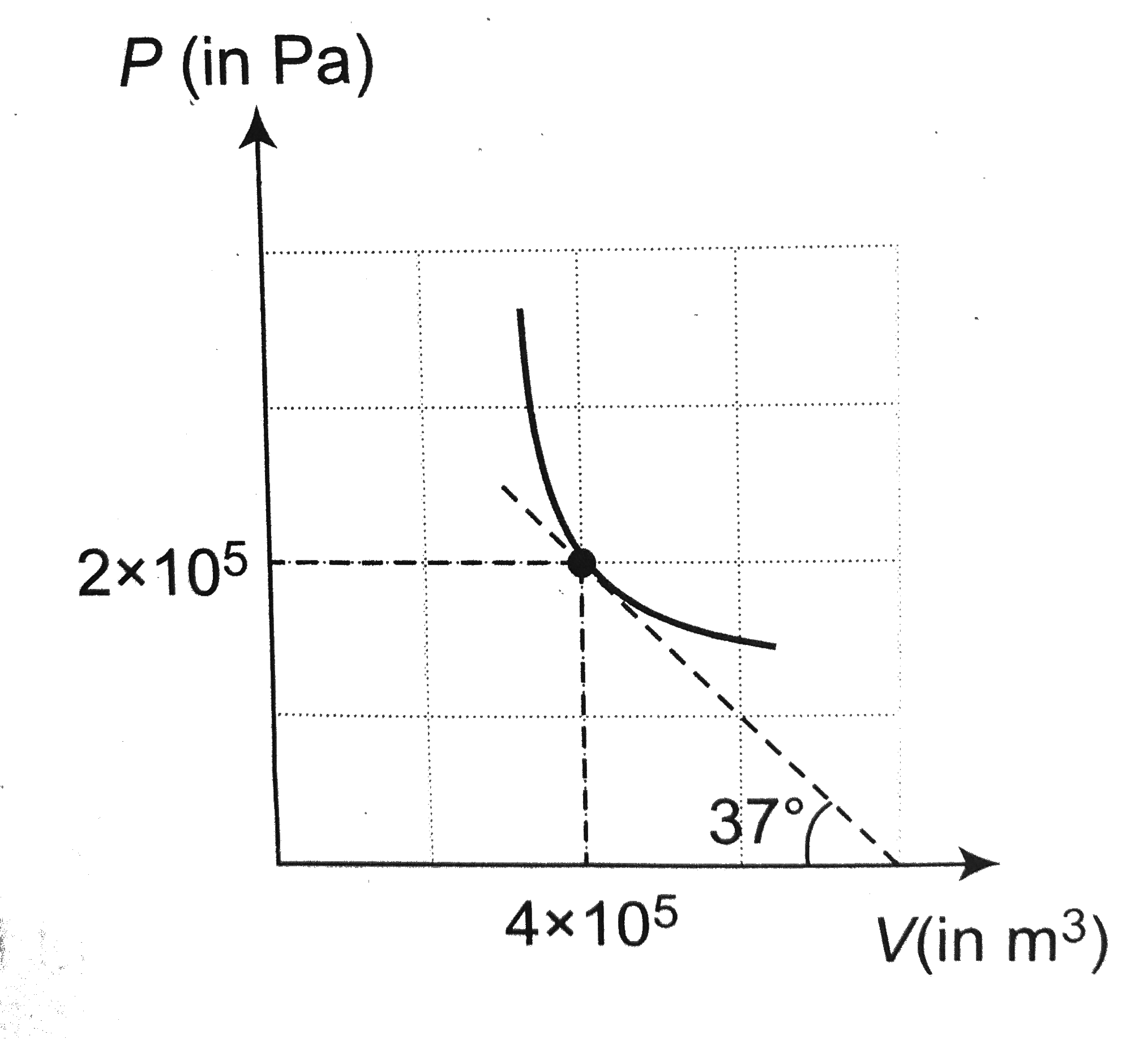
View SolutionP-V graph for an ideal gas undergoing polytropic process PVm=constant is shown here. Find the value of m.
View SolutionOne mole of an ideal monatomic gas undergoes a process described by the equation PV3= constant. The heat capacity of the gas during this process is
View Solution
