Three point masses are attached by light inextensible strings of various lengths to a point O on the ceiling. All of the masses swing round in horizontal circles of various radii with the same angular frequency ω (one such circle is drawn in the shown figure.) Then pick up the correct statement.
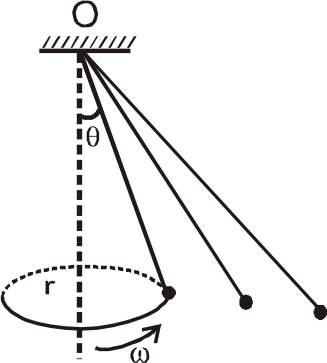
The vertical depth of each mass below point of suspension from ceilling is different.
The raduis of horizontal circular path of each mass is same.
All masses revolve in the same horizontal plane.
All the particles must have same mass.
For conical pendulum of length l , mass m moving along horizontal circle as shown
Tcosθ=mg.....(1)
Tsinθ=mω2lsinθ.......(2)
From equation (1) and equation (2) , lcosθ=gω2
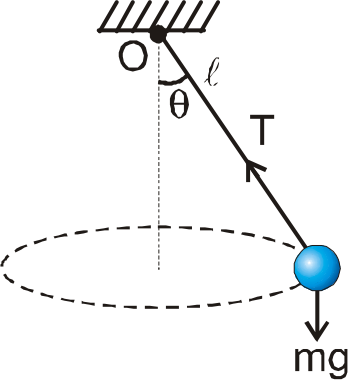
lcosθ is the vertical distance of bob below O point of suspension. hence if ω of all three pendulums are same, they shall revolve in same horizontal plane.
Alternate:
If we remember that time period T of conical pendulum is
T=2π√Lg where L is the vertical depth of bob below point of suspension. if T is same for three pendulums even L shall be also same. hence all three particles shall revolve in same horizontal plane.
Topper's Solved these Questions
Similar Questions
A radioactive element decays by β−emission. A detector records n beta particles in 2s and in next 2s it records 0.75n beta particles. Find mean life correct to nearest whole number. Given ln |2|=0.6931, ln |3|=1.0986.
06:04View SolutionWhen p−n junction diode is forward biased then
View SolutionA bob of mass m attached to an inextensible string of length I is suspended from a vertical support. The bob rotates in a horizontal circle with an angular speed ω red/s about the vertical. About the point of suspension:
07:16View SolutionA small ball of mass m suspended from the celling at a point O by a thread of length l moves along a horizontal circle with a constant angular velocity omega . .
03:32View SolutionA bob of mass 2kg is suspended from point O of a core with an inextensible string strinng of length sqrt(3)m . It is moving in horizontal circle over the surface of cone as shown in the figure. Then :(g=10m//s^(2))
04:34View SolutionThree masses of small size are attached by light inextensible strings of various lengths to a point O on the ceiling. All of the masses swing round in horizontal circles of various radii with the same angular frequency ω (one such circle is drawn in the shown figure.) Then pick up the correct statement.
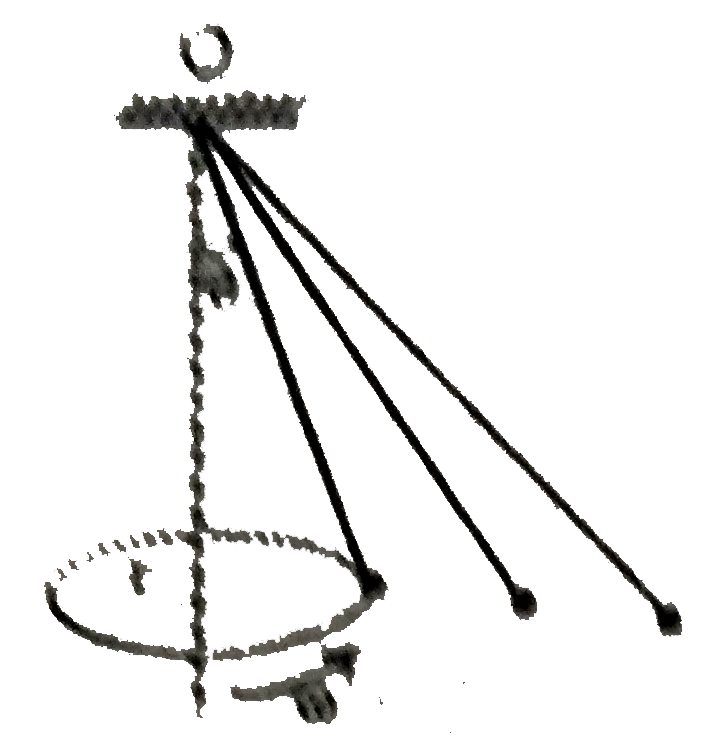 03:55View Solution
03:55View SolutionThree balls each of mass 1 kg are attached with three strings each of length 1 m as shown in figure. They are rotated in a horizontal circle with angular velocity ω=4rad s−1 about point O. Match the following columns.
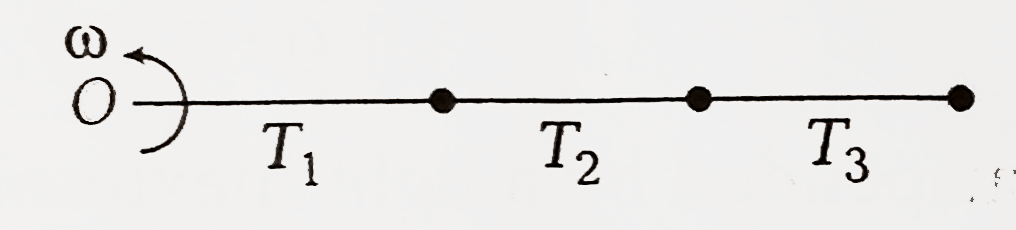 View Solution
View SolutionA particle of mass m attached to an inextensible light string is moving in a vertical circle of radius r. The critical velocity at the highest point is v_( 0) to complete the vertical circle. The tension in the string when it becomes horizontal is
03:21View SolutionA bob of mass m attached to an inextensible string of length l is suspended from a vertical support. The bob rotates in a horizontal circle with an angular speed omega rad/s about the vertical support. About the point of suspension
View SolutionA bob of mass m attached to an inextensible string of length I is suspended from a vertical support. The bob rotates in a horizontal circle with an angular speed ω red/s about the vertical. About the point of suspension:
View SolutionOne end of string of length 1m is tied to a body of mass 0.5 kg. It is whirled in a vertical circle as shown in figure. If the angular frequency of the body is 4rad/sec
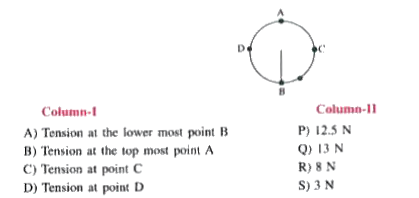 04:32View Solution
04:32View SolutionA Small ball of mass m suspended from the ceiling at a point O by a thread of length l moves along a horizontal circle with a constant angular velocity ω. Which of the following statements(s) is/are correct ?
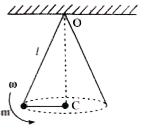 03:58View Solution
03:58View SolutionThree balls each of mass 1 kg are attached with three strings each of length 1 m as shown in figure. They are rotated in a horizontal circle with angular velocity omega=4"rad s"^(-1) about point O. Match the following columns.
View SolutionThree balls each of mass 1 kg are attached with three strings each of length 1 m as shown in figure. They are rotated in a horizontal circle with angular velocity ω=4rad s−1 about point O.find the tensions .
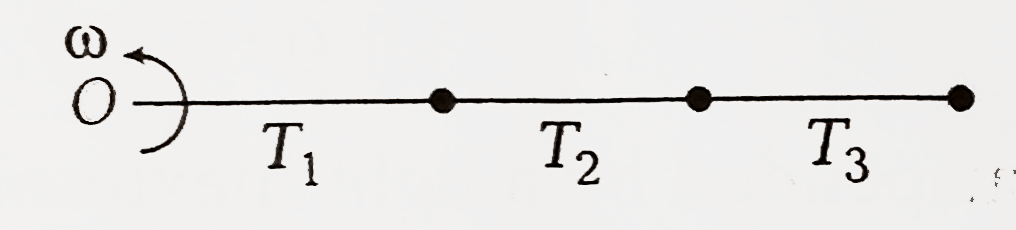 06:24View Solution
06:24View SolutionA bob of mass m attached to an inextensible string of length l is suspended from a vertical support. The bob rotates in a horizontal circle with an angular speed ω rad/s about the vertical. About the point of suspension
11:40View Solution

