A particle of mass m collides elastically with the pan of mass (M = 2m) of a spring balance, as shown in figure. Pan is in equillibrium before collision. Spring constant is k and speed of the particle before collision is v0 . Answer the following three questions regarding this collision.
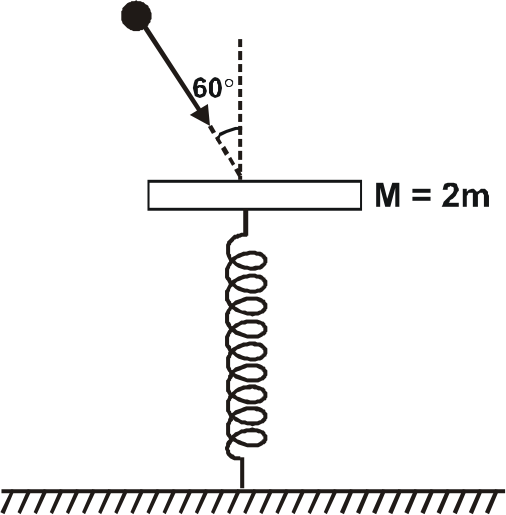
Maximum height attained by the particle from the point of collision after collision is
v2016g
v208g
v2036g
v2072g

v1+v2=V0/2
2mv2−mv1=mv02⇒v1=v06,v2=v03
Maximum compression =v2√K2m=√2mkv03
Maximum height =v212g=v2072g
minimum kinetic energy =12m(√3v02)2=3mv208
Topper's Solved these Questions
Similar Questions
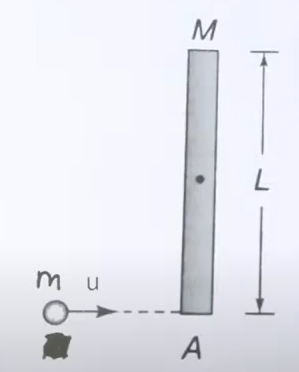
A particle of mass m and speed u collides elastically with the end of a uniform rod of mass M and length L as shown. If the particle comes to rest after collision, find mM
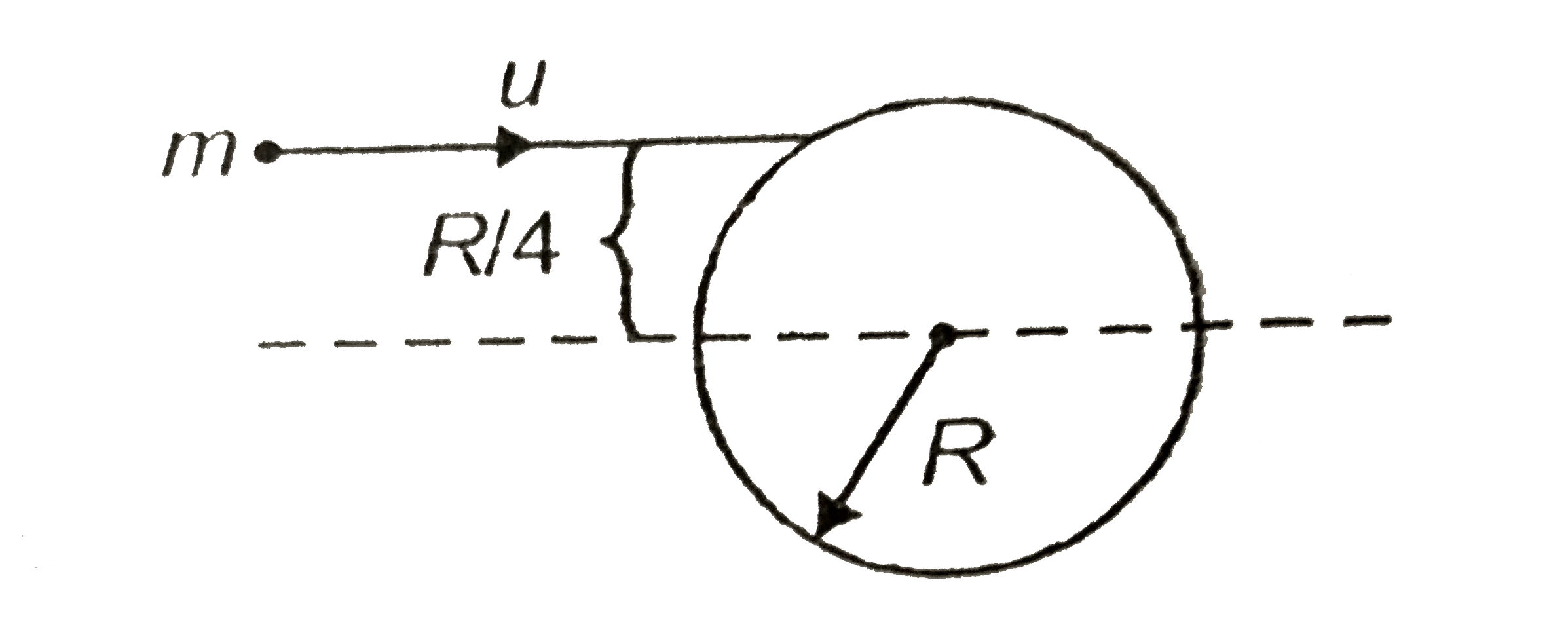
View SolutionA particle of mass m strikes a disc of radius R and mass m with a speed u as shown in the figure. What is the speed of the particle just after the collision if the collision is perfectly inelastic ?
View Solution
Knowledge Check
A particle of mass m collides elastically with the pan of mass (M = 2m) of a spring balance, as shown in figure. Pan is in equillibrium before collision. Spring constant is k and speed of the particle before collision is v0 . Answer the following three questions regarding this collision.
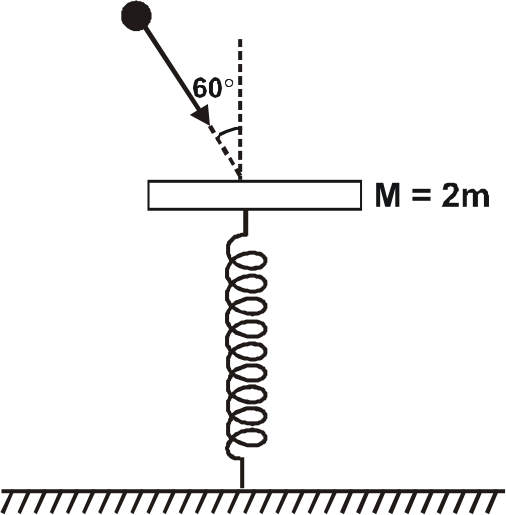
Maximum compression in the spring after the collision theA√2mkv03B√2m3kv0C√m3kv0D√mkv0A particle of mass m collides elastically with the pan of mass (M = 2m) of a spring balance, as shown in figure. Pan is in equillibrium before collision. Spring constant is k and speed of the particle before collision is v0 . Answer the following three questions regarding this collision.
Minimum kinetic energy of the particle after collision isAmv208B3mv208C3mv204Dmv202A particle of mass m moving with speed V collides eleastically with another particle of mass 2mFind speed of smaller mass after head on collision
Av3B−v3C2v3D−2v3
A particle of mass m1 collides elastically with a stationary particle of mass m2(m1>m2). Find the maximum angle through which the striking particle may deviate as a result of the collision.
View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 3 m at rest. Loss of KE of system in the collision is
View SolutionA particle of mass m moving with horizontal speed 6m/s as shown in the figure. If m<<M then for one - dimensional elastic collision , the speed of lighter particle after collision will be

View SolutionA particle of mass m moving with horizontal speed 6m/s as shown in the figure. If m<<M then for one - dimensional elastic collision , the speed of lighter particle after collision will be

View SolutionA particle of mass m, collides with another stationary particle of mass M. If the particle m stops just after collision, then the coefficient of restitution for collision is equal to
View Solution
