A nonconducting ring of uniform mass m, radius b and uniform linear charge density $λ$ is suspended as shown in figure in a gravity free space. There is uniform coaxial magnetic field $B_{0}$ , pointing up in a circular region of radius 'a' $(< b)$ . Now if this field is switched off, then:-

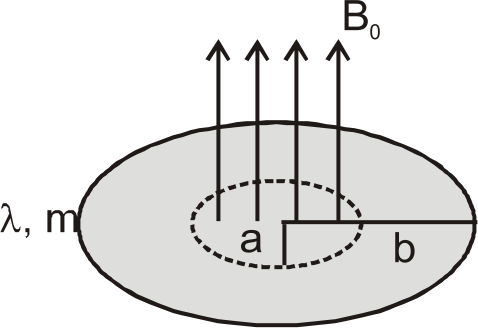
There will be induced electric field on periphery of ring, in anticlockwise sense when seen from above

Induced electric field imparts angular momentum of magnitude $λ π a^{2} b B_{o}$

Final angular velocity of ring will be more if time taken to switch of the field $B_{o}$ is small

Final angular velocity will always be independent of time taken to switch off the field $B_{o}$

Text Solution

Verified by Experts

Changing magnetic field (at switching off $B_{0}$ to zero) induced electric field in such a way to restore the upwards flux, hence anticlockwise (E) as seen from above
$\int \to E . \to d l = - \frac{d ϕ}{d t} = - π a^{2} \frac{d B}{d t} = \int E d l$
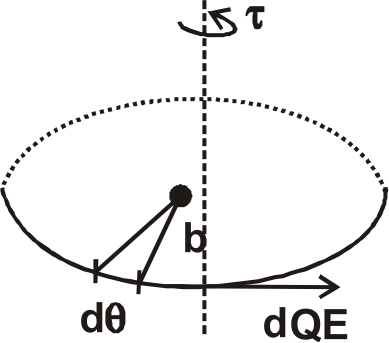
There is force on small element dQ of ring, tangentially Now this force produces torque about axis of ring to rotate in anticlockwise sense, so
$τ = \int d Q E \times b = \int λ d l E b = λ b \int E d l = λ b π a^{2} \frac{d B}{d t}$
So impulse or torque
$\int τ d t = λ b π a^{2} \int_{B_{0}}^{2} d B = \int τ d t = λ b π a^{2} B_{0}$
$L_{f} - L_{i} = Δ L = \int τ d t = λ b π a^{2} B_{0} = I ω$ (in magnitude)
It is indpendent of time taken $I ω_{f} - I ω_{i} = λ b π a^{2} B_{0}$
where I is moment of inertia
So, $ω_{f} = \frac{λ b π a^{2} B_{0}}{m R^{2}}$

Updated on:21/07/2023