A line charge with linear charge density λ is wound around an insulating disc of mass M and radius R, which is then suspended horizontally as shown in Fig. 3.90, so that it is free to rotate. In the central region, of radius a, there is a uniform magnetic field B0, pointing up. Now the magnetic field is switched off, which causes the disc to rotate.
Find the angular speed with which the disc starts rotating.
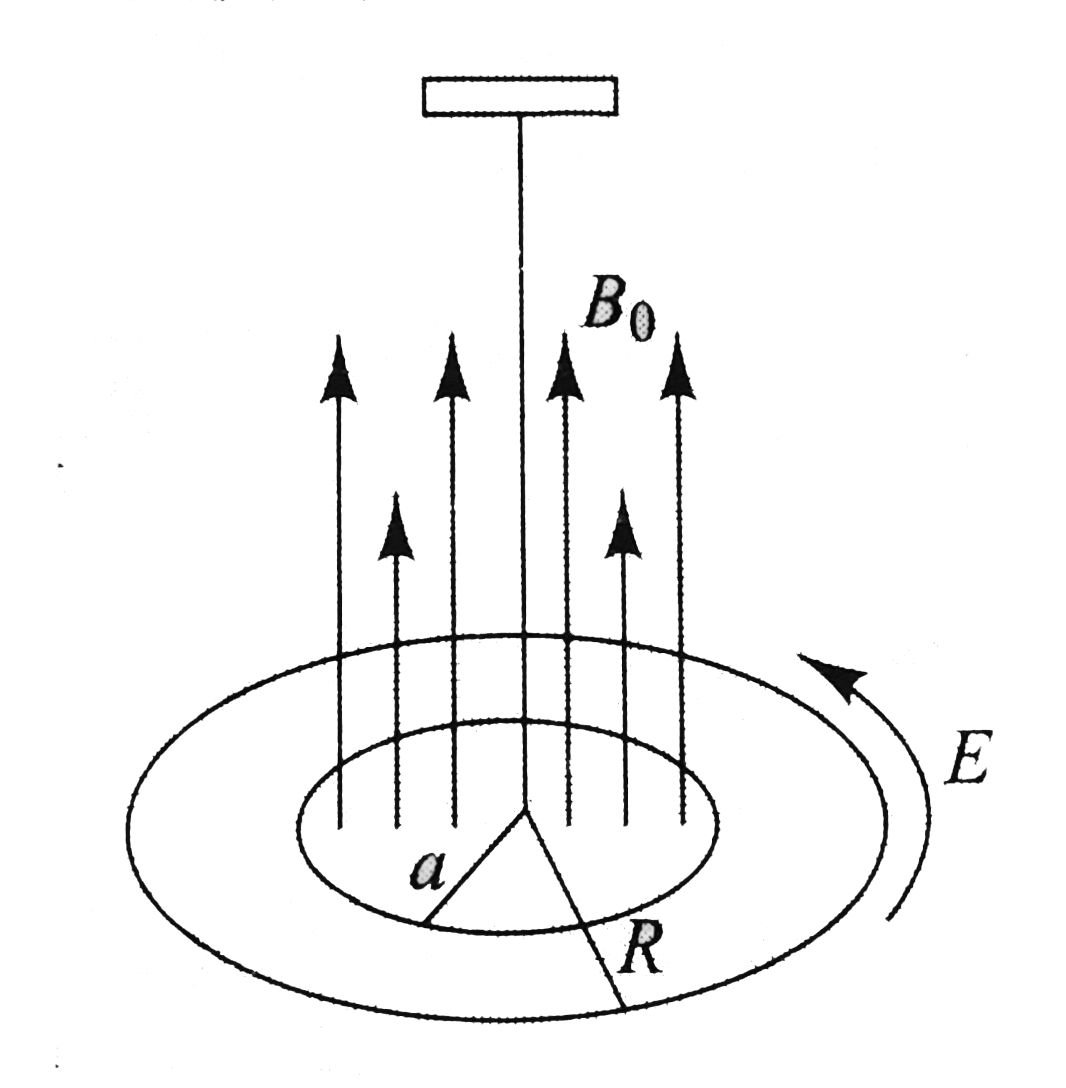
The induced electric field E due to the changing magnetic field is given by (from Faraday's law)
→ E.2πr=−πa2dBdt → E=−a22RdBdt
Hence, induced electric field is tangential to the disc as shown in Fig. 3.90 and its magnitude is E=a22RdBdt.
This electric field causes the disc to rotate. Now torque on the disc is τ=(λpuR)ER=πlambda2RdBdt.
Angular impulse:
L=∫τdt=∫πλa^(2)R(dB)/(dt)dt = piλa^(2)Rint dB = pi alpha a^(2)RB_(0)<br>NowL = Iomega<br>rarrpiλa^(2)RB_(0) = (MR^(2))/(2)omegararromega = (2pi lambda a^(2)B_(0))/(MR)
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Solved Example
5 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise 3.1
15 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
Similar Questions
A disc of mass m and radius R moves in the x−y plane as shown in Fig. The angular momentum of the disc about the origin O at the instant shown is

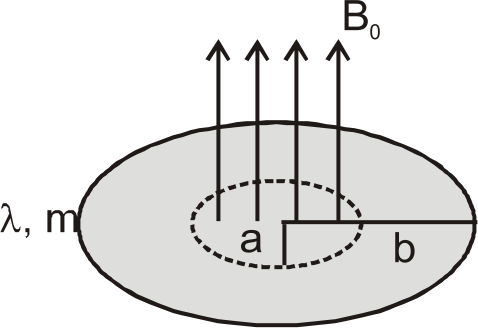
View SolutionA nonconducting ring of uniform mass m, radius b and uniform linear charge density λ is suspended as shown in figure in a gravity free space. There is uniform coaxial magnetic field B0, pointing up in a circular region of radius 'a' (<b). Now if this field is switched off, then:-
View SolutionA charged particle of mass m and charge q describes circular motion of radius r in a uniform magnetic field of strength B the frequency of revolution is
View SolutionCharge Q is uniformly distributed on the rim of a thin insulating disc of mass m which is initially at rest and placed on a smooth horizontal surface. What will be the angular velocity of the disc if a magnetic field B, perpendicular to the plane of the disc is switched on ?

View SolutionA ring of mass m, radius r having charge q uniformly distributed over it and free to rotate about its own axis is placed in a region having a magnetic field B parallel to its axis. If the magnetic field is suddenly switched off, the angular velocity acquired by the ring is:
View SolutionFind the ratio of magnetic dipole moment and magnetic field at the centre of a disc. Radius of disc is R and it is rotating at constant angular speed o about its axis. The disc is insulating and uniformly charged
View SolutionA copper disc of radius 0.1 m is rotated about its natural axis with 10 rps in a uniform magnetic field of 0.1 T with its plane perpendicular to the field, The emf induced across the radius of the disc is
View SolutionA: magnetic field is produced by moving charges(s).
R: The magnetic field in the central region of a solenoid is uniform.
View SolutionA uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is

View SolutionA disc of radius 0.2m is rolling with slipping on a flat horizontal surface, as shown in Fig. The instantaneous centre of rotation is (the lowest contact point is O and centre of disc is C)
View Solution
