Inscribed Angle Theorem
The measure of an inscribed angle is half of the measure of the arc intercepted by it.
Given : In a circle with centre O, ∠BAC is inscribed in an arc BAC. ∠BAC intercepts are BXC of the circle.
To prove :m∠BAC=12 m ( arc BXC ) .
Proof : There arise three cases as shown in parts (a) , (b) , (c ) of the figure.
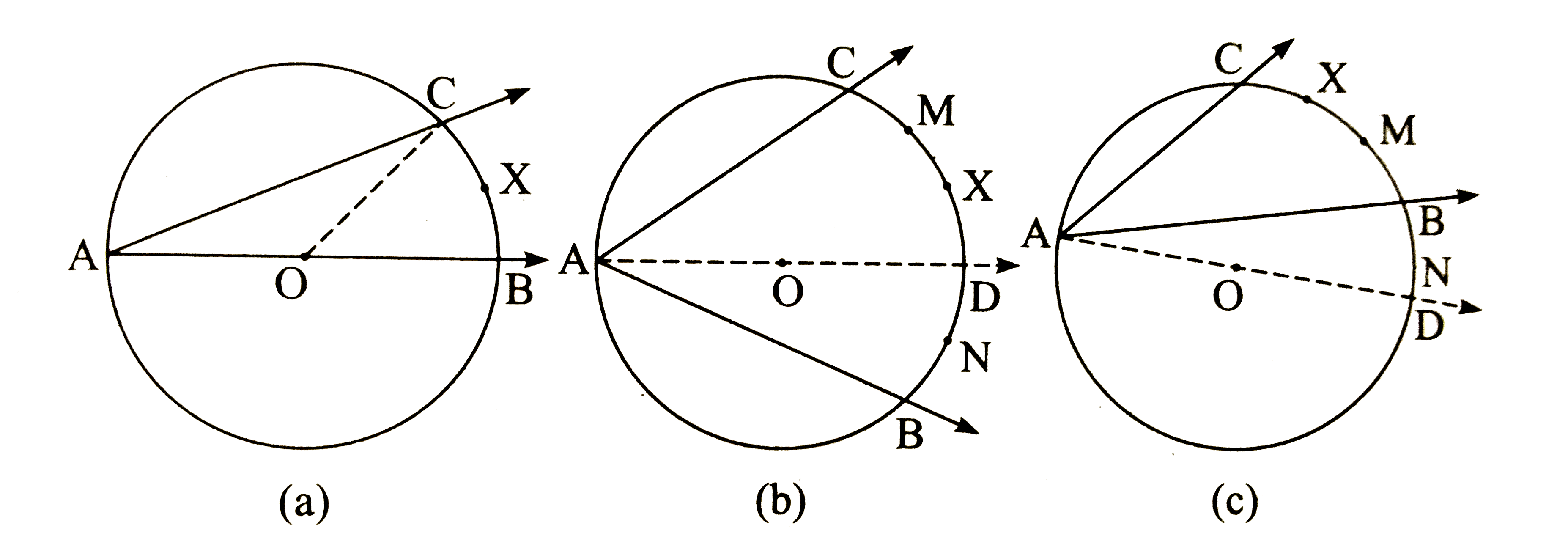
Case 1 : The centre is on the angle [as in figure (a) ]
In this case, join C to O .
ΔOAC is isosceles with OA = OC .
Let ∠OAC=∠OCA=p,
By remote interior angles theorem,
∠BOC=∠OAC+∠OCA
∠BOC=p+p=2p=2∠BAC
∴∠BAC=12∠BOC
But ∠BOC= m ( arc BXE ) ....(Definition of measure of minor arc )
∴∠BAC=12m (arc BXC ).
Case 2 :
The centre is in the interior of the angle [as in figure (b) ]. In this case let D be the other endpoint of the diameter drawn through A. Let arc CMD be the one intercepted by ∠CAD, and let arc BND be the one intercepted by ∠DAB .
Then as proved in the first situation, we have
∠CAD=12m(arc CMD)
and ∠DAB=12 m (arc BND)
∴∠CAD+∠DAB=12 m (arc CMD) +12m (arc BND)
∴m∠BAC=12[ m ( arc (CMD ) + m (arc BND) ]
=12m (arc BXC ) .
Case 3 :
The cnetre is in the exterior of the angle [ as n figure ( c ) ] . Again let D be other endpoint of the digameter drawn through A. Let arc CMD be the one intercepted by ∠CAD and let arc BND be the one intercepted by ∠DAB .
Then as proved in the first situation , we have,
∠CAD=12m( arc CMD )
and ∠DAB=12m (arc BND)
∴∠CAD−∠DAB=12 m (arc CMD ) −12m (arc BND)
∴∠BAC=12[ m ( arc CMD ) - m ( arc BND ) ]
=12 m (arc BXC ) .
Topper's Solved these Questions
- THEOREMS BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - THEOREMS EXERCISE - PYTHAGORAS THEOREM
4 Videos
- STATISTICSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - STATISTICSEXERCISE - EXAMPLES FOR PRACTICE (MCQs)
35 Videos
- TRIGONOMETRYBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - TRIGONOMETRYEXERCISE - CHALLENGING QUESTIONS
6 Videos
Similar Questions
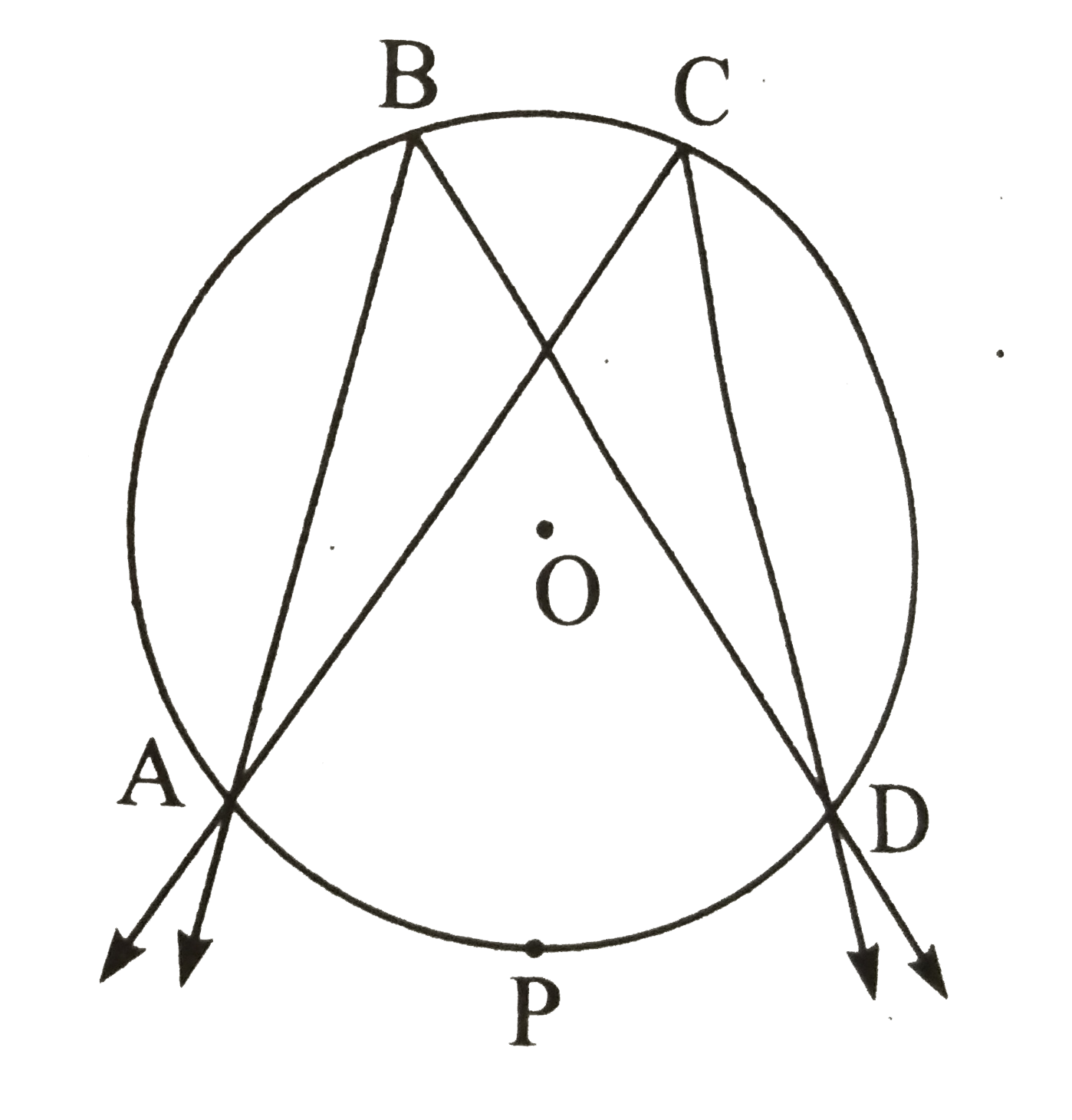
Corollaries of inscribed angle theorem :
Angle inscribed in the same arc arc contruent
Given : (1) A circle with centre O
(2) ∠ABD and ∠ACD are inscribed in arc ABC and intercepts arc APD.
To prove : ∠ABD≅∠ACD
View SolutionIn the figure, O is the centre of the circle. Seg AC is the diameter ∠ABC is inscribed in arc ABC and intercepts arc AMC then prove ∠ABC=90∘

View Solution
Knowledge Check
∠ACB is inscribed in arc ACB of a circle with centre O . If ∠ACB=65∘ , find m ( arc ACB ) .
A65∘B130∘C295∘D230∘The radian measure of the angle, subtends at the centre of a circle by an arc whose length is twice the diameter of the circle, is
A2Bπ2CπD4
Theorem of angle between tangent and secant
If an angle has its vertex on the circle, its one side touches the circle and the other intersects the circle in one more point, then the measure of the angle is half the measure of its intercepted arc .
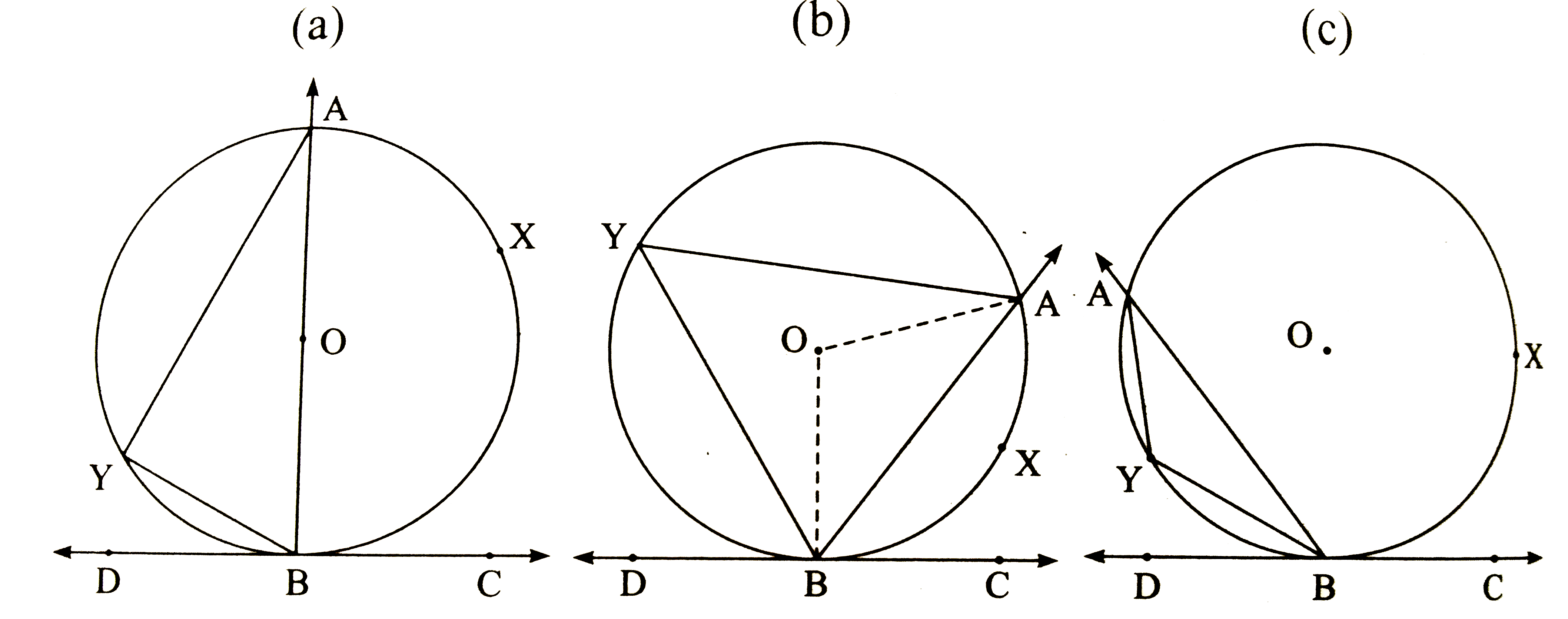
Given : Let O be the centre of the circle. Line DBC is tangent to the circle at point B. Seg BA is a chord of the circle. Point X of the circle is on C side of line BA and point Y of the circle is on D side of line BA.
To prove : m ∠ABC=12m(arcAXB).
View SolutionTheorem 2 : The no. of Radians in an angle subtended by an arc of a circle at the centre = arc/radius
View SolutionFind tge degree measure of the angle subtended at the centre of a circle of diameter 60 cm by an arc of length 16.5 cm.
View SolutionBC is a chord to a circle with centre O. A is a point on major are BC as shown in the below figure. What is the value of ∠BAC+∠OBC ?
View SolutionIn the figure , in a circle with centre O, length of chord AB is equal to the radius of the circle. Find the measure of each of the following :
(1) ∠AOB
(2) ∠ACB
(3) arc AB
(4) arc ACB

View SolutionIf the angle subtended at the center the circle by arc BC is 100∘. Then calculate the value of ∠BAC.
View Solution
