Two circles intersect each other in points A and B. Seg AB is the chord of both the circles . Point C is in the exterior point of both the circles on the line AB. From the point C tangents are drawn to the circles touching at M and N as shown. Completely the following to prove CM= CN.
Proof :
CM2=CA×□ ....( □) ....(1)
CN2=□×CB ...(Tangent secant segment property ) ....(2)
∴ From (1) and (2),
CM2=□
∴CM=CN
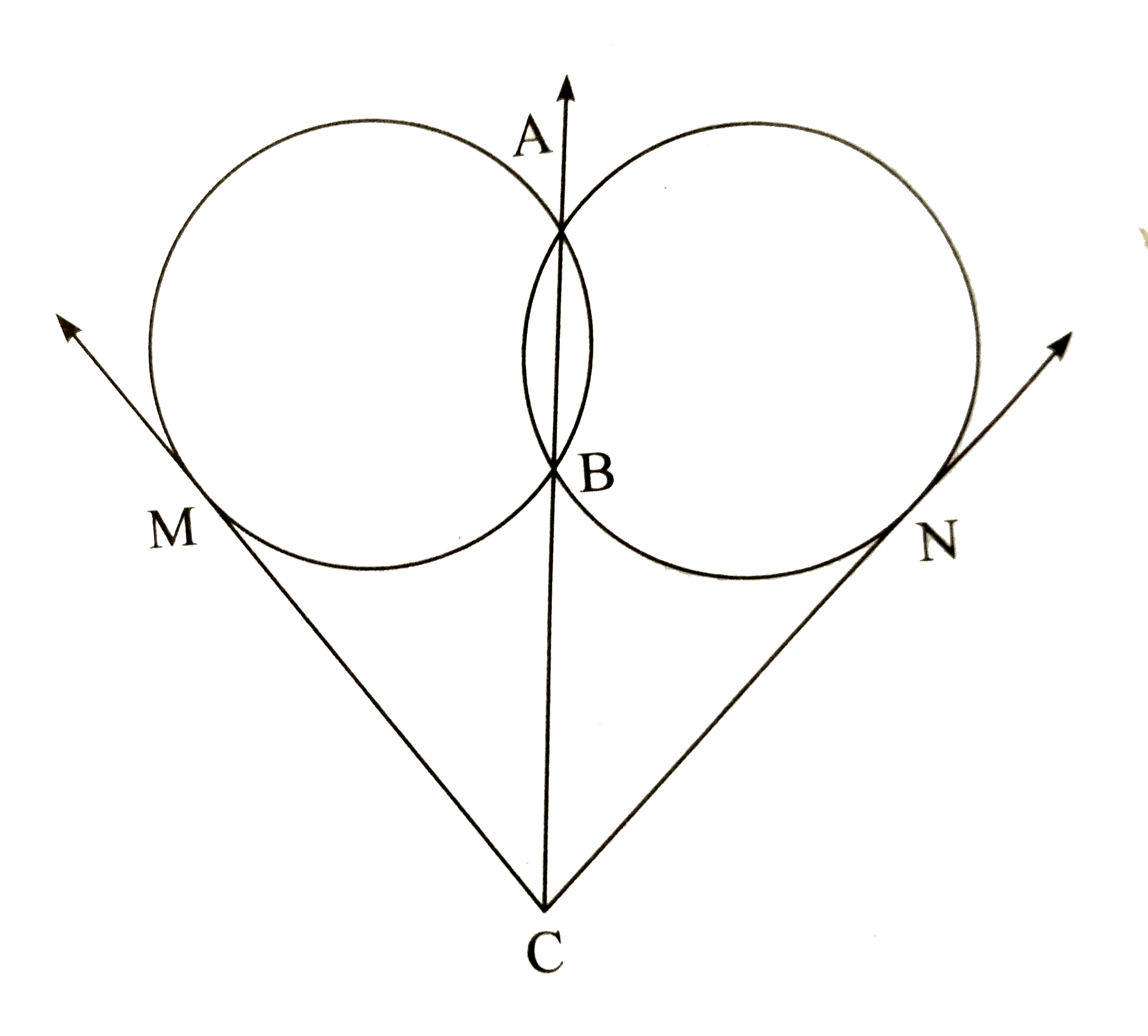
The correct Answer is:CM2=CA×CB …(1)
….(Tangent secant segment property)
CN2=CA×CB ….(2)
from (1) and (2).
CM2=CN2
∴CM=CN.
Step by step video & image solution for Two circles intersect each other in points A and B. Seg AB is the chord of both the circles . Point C is in the exterior point of both the circles on the line AB. From the point C tangents are drawn to the circles touching at M and N as shown. Completely the following to prove CM= CN. Proof : CM^(2) = CA xx square ....( square ) ....(1) CN^(2) = square xx CB ...(Tangent secant segment property ) ....(2) :. From (1) and (2), CM^(2) = square :. CM = CN by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - PRACTICE SET 3.1
9 Videos
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - PRACTICE SET 3.2
8 Videos
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - ASSIGNMENT 4.5
8 Videos
- CHALLENGING QUESTIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve any one of the following subquestions :
1 Videos
- COORDINATE GEOMETRY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - COORDINATE GEOMETRY EXERCISE - Assignment 6.5
13 Videos
Similar Questions
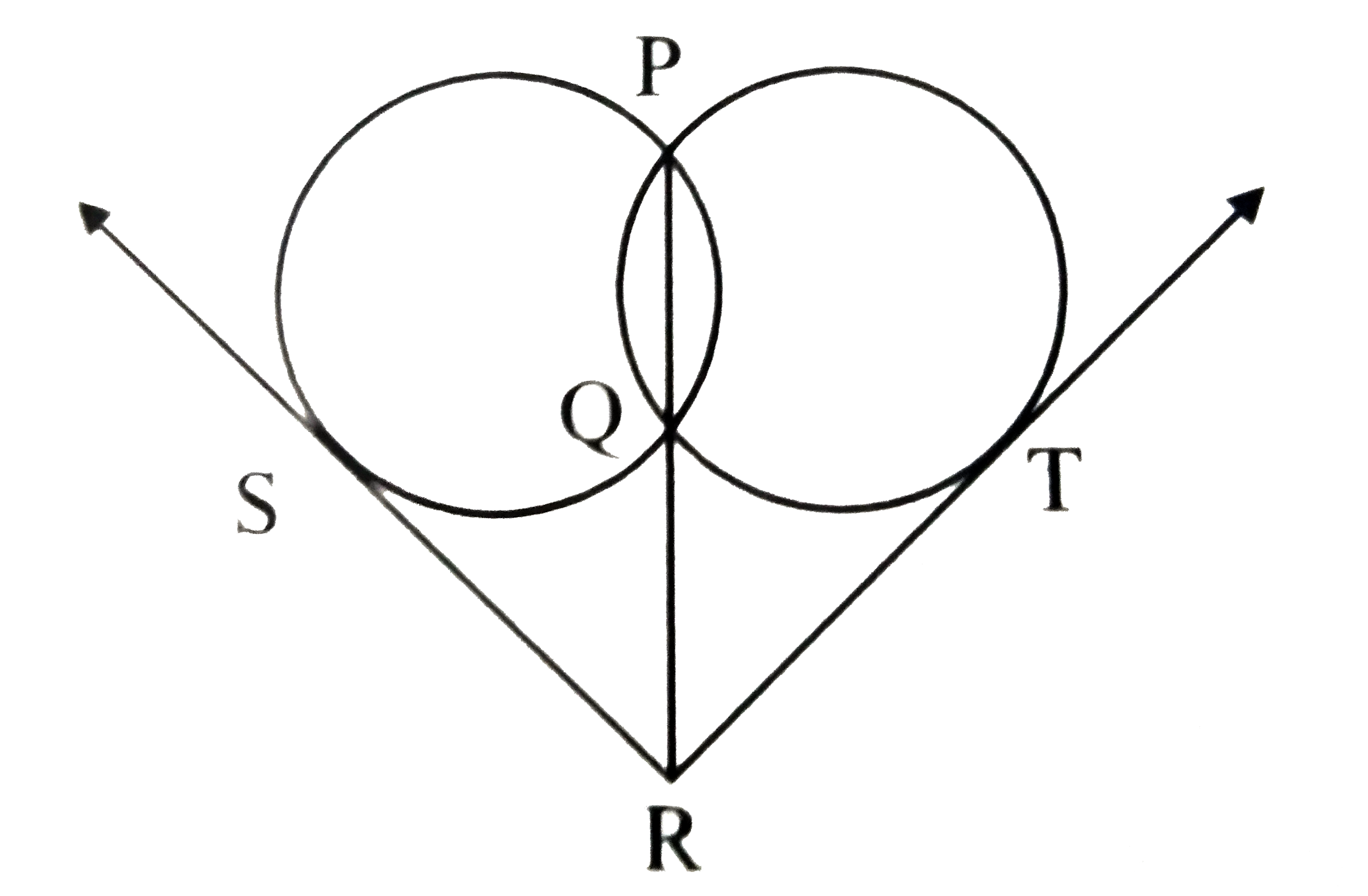
In the figure, two circles intersect each other in points P and Q. If tangent from point R touch the circles at S and T, then prove that RS=RT.
View SolutionTwo circles intersect each other at the points P and Q. Two straight lines through P and Q intersect one circle at the points A and C and the other circle at B and D. Prove the AC|| BD
View Solution
Knowledge Check
Two circles intersect each other at the points A and B, A straight line parallel to AB intersects the circles at C, D, E and F. If CD = 4.5 cm, then the measure of EF is
A1.50cmB2.25cmC4.50cmD9.00cm
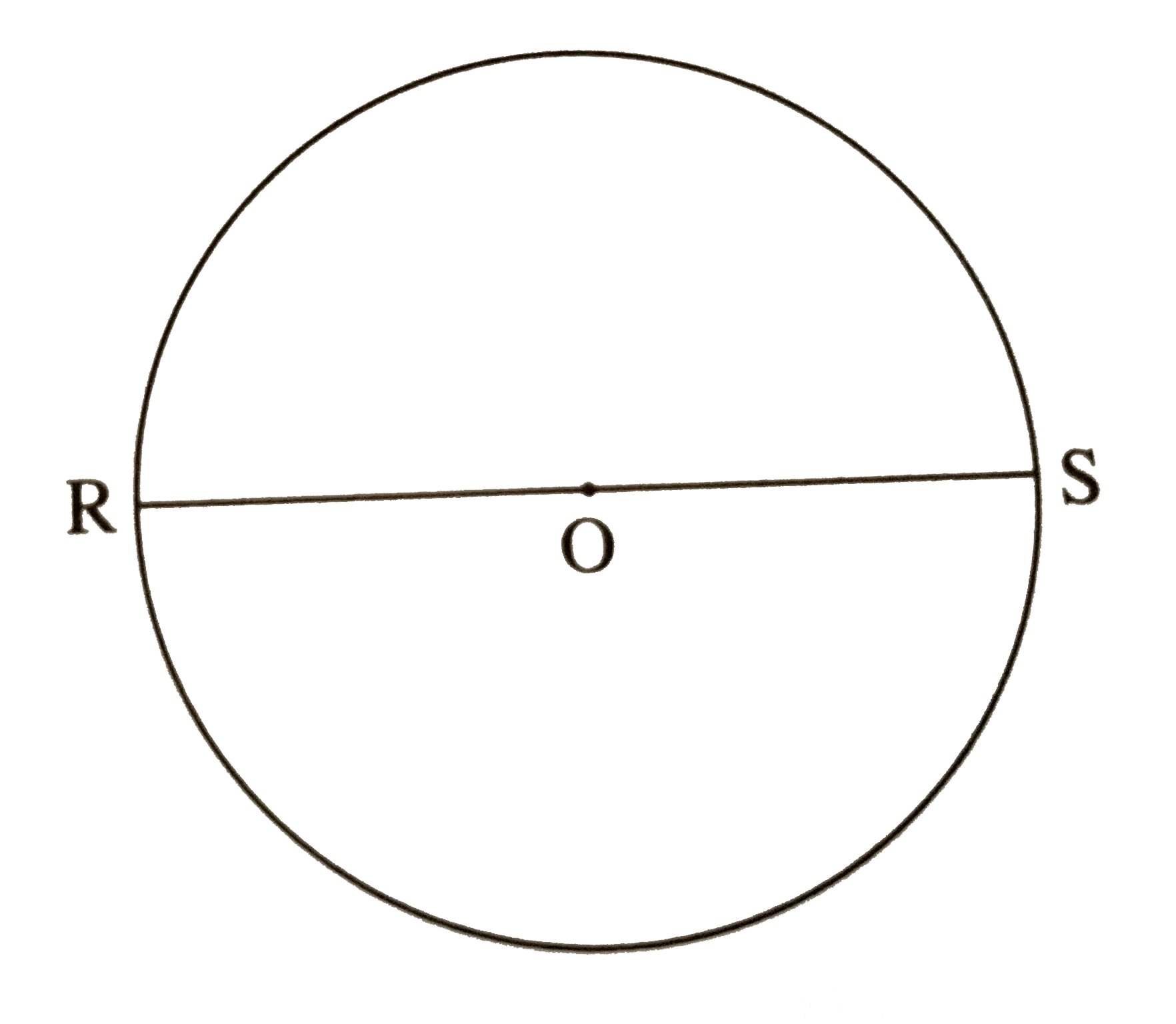
In figure, seg RS is a diameter of the circle with centre O. Point T lines in the exterior of the circle. Prove that ∠RTS is an acute angle.
View SolutionIn the figure, O is the centre of the circle . Seg AB is the diameter at the point C on the circle the tangent CD is drawn. Line BD is a tangent to the circle at point B. Show that seg OD ∣∣ chord AC.
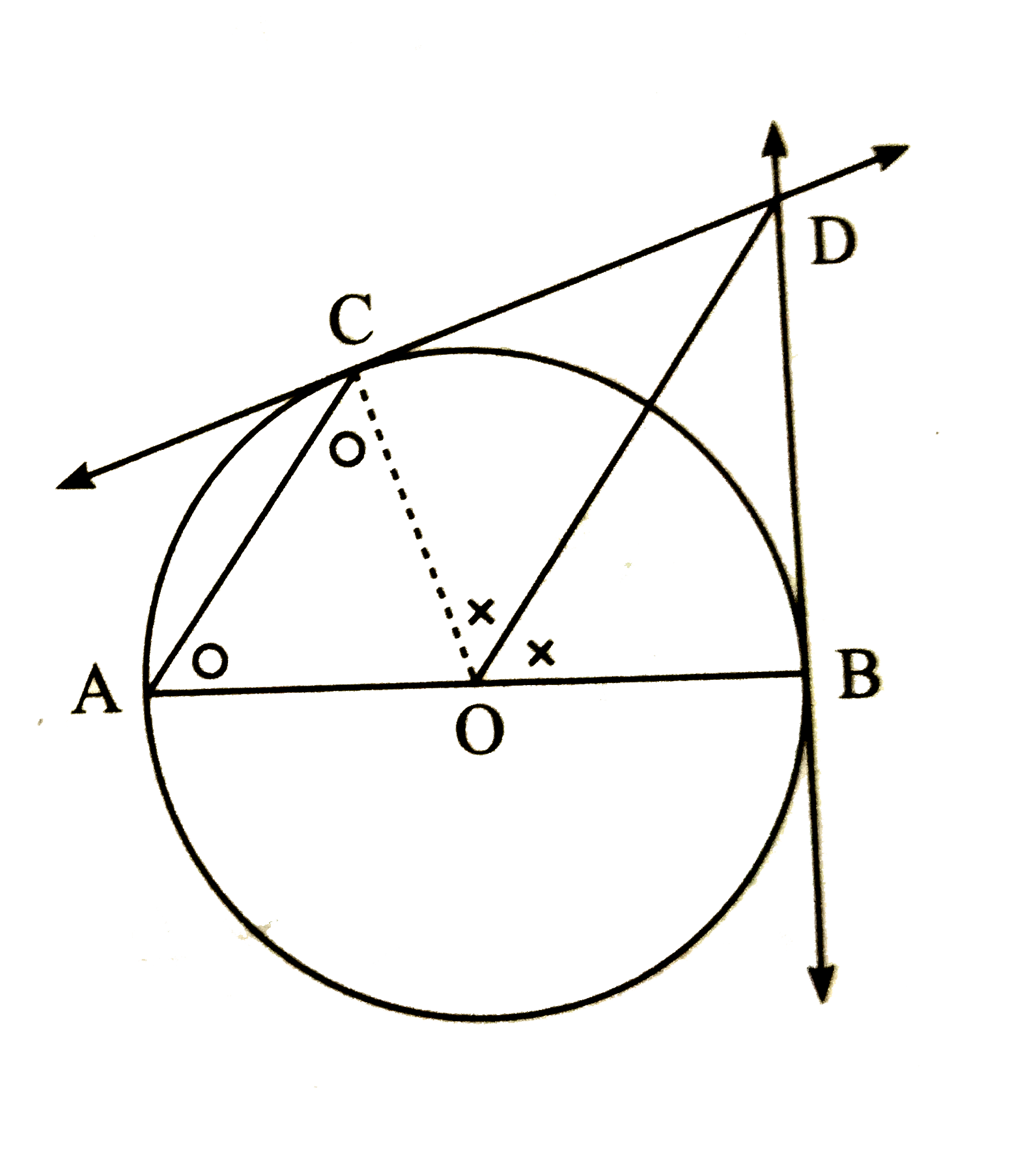
View SolutionTwo circles intersect each other at point P and Q. Secants drawn through p and Q intersect the circles at points A,B and D,C
Prove that :∠ADC+∠BCD=180∘
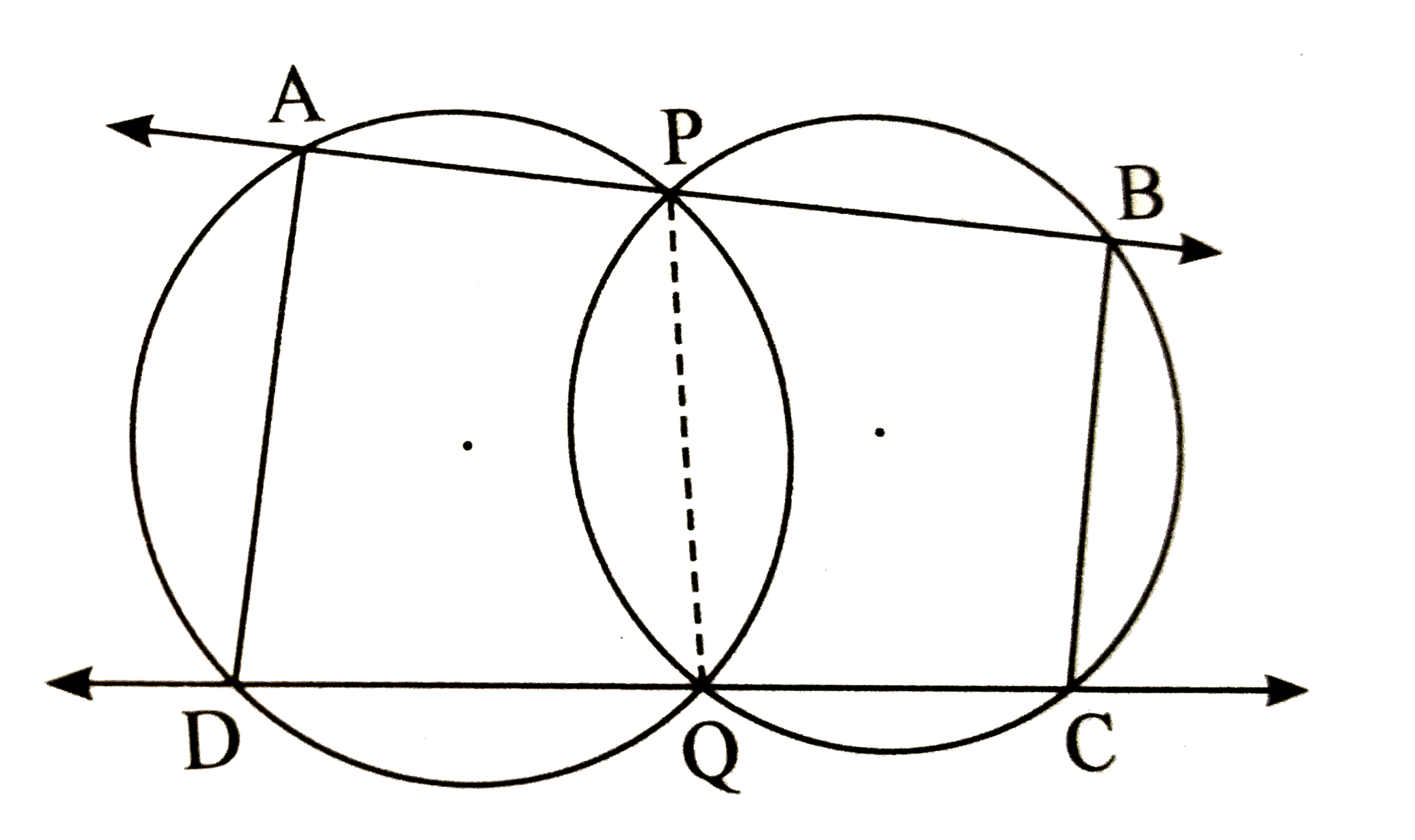
View SolutionTwo circles touch each other externally at point P. A common tangent AB is drawn touching the circles at A and B. Find ∠APB.
View SolutionIn the figure, two circles intersect each other at points A and B . C is a point on the smaller circle. Secant CA and secant CB of the smaller circle intersect the bigger circle at points D and E respectively then prove : seg DE ∣∣ line CF
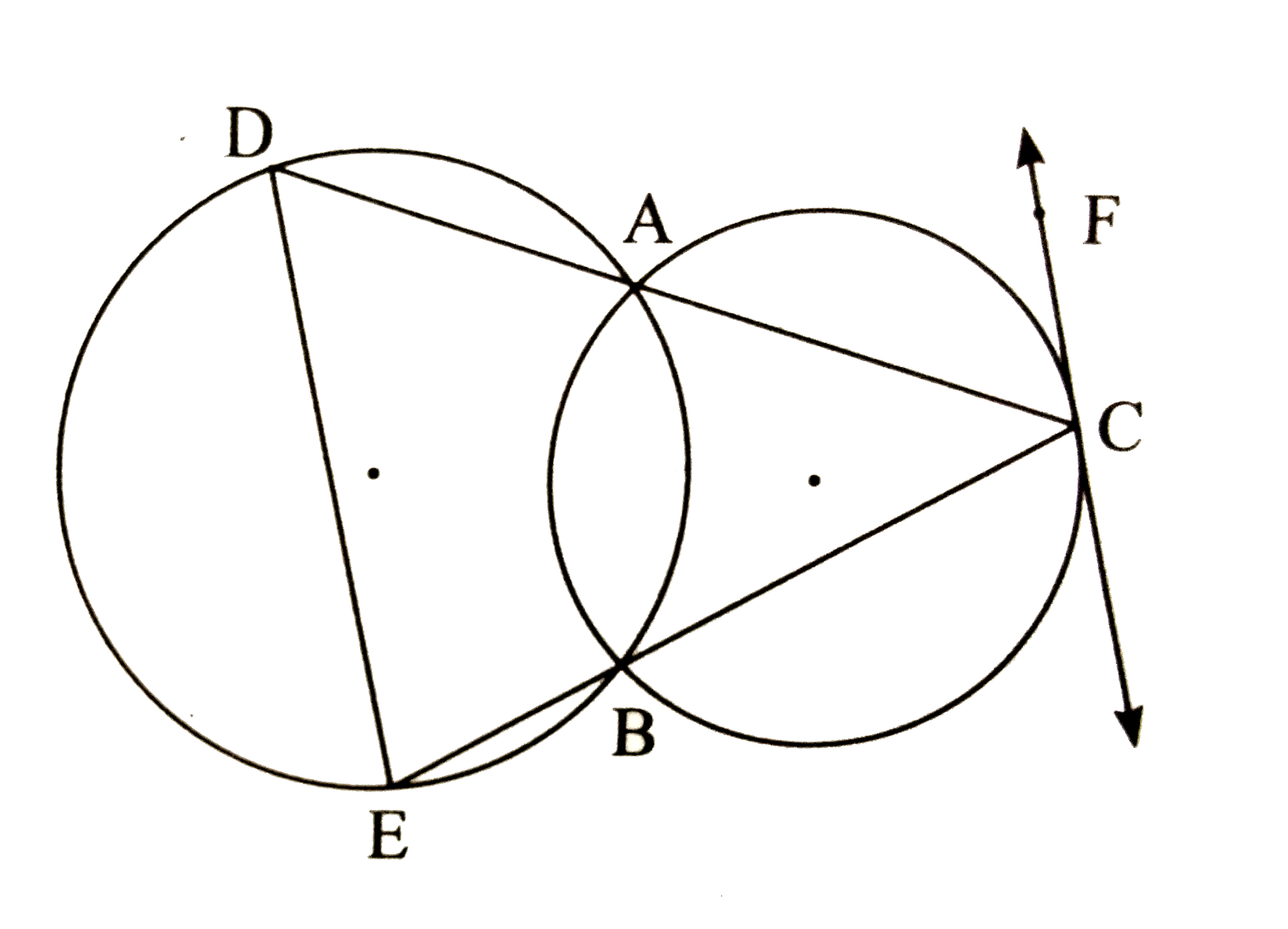
View SolutionIf from any point on the common chord of two intersecting circles, tangents be drawn to the circles, prove that they are equal.
View SolutionIn figure, two circles intersect each other at points A and E. Their common secant through E intersects the circles at points B and D. The tangents of the circles at points B and D intersect each other at point C. Prove that □ ABCD is cyclic.

View Solution
