Prove the any three points on a circle cannot be collinear .
Step by step video & image solution for Prove the any three points on a circle cannot be collinear . by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - Challenging Questions
10 Videos
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - PRACTICE SET 3.5
6 Videos
- CHALLENGING QUESTIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve any one of the following subquestions :
1 Videos
- COORDINATE GEOMETRY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - COORDINATE GEOMETRY EXERCISE - Assignment 6.5
13 Videos
Similar Questions
Knowledge Check
There are n points in a plane, No three being collinear except m of them which are collinear. The number of triangles that can be drawn with their vertices at three of the given points is
An−mC3BnC3−mC3CnC3−mDNone of these
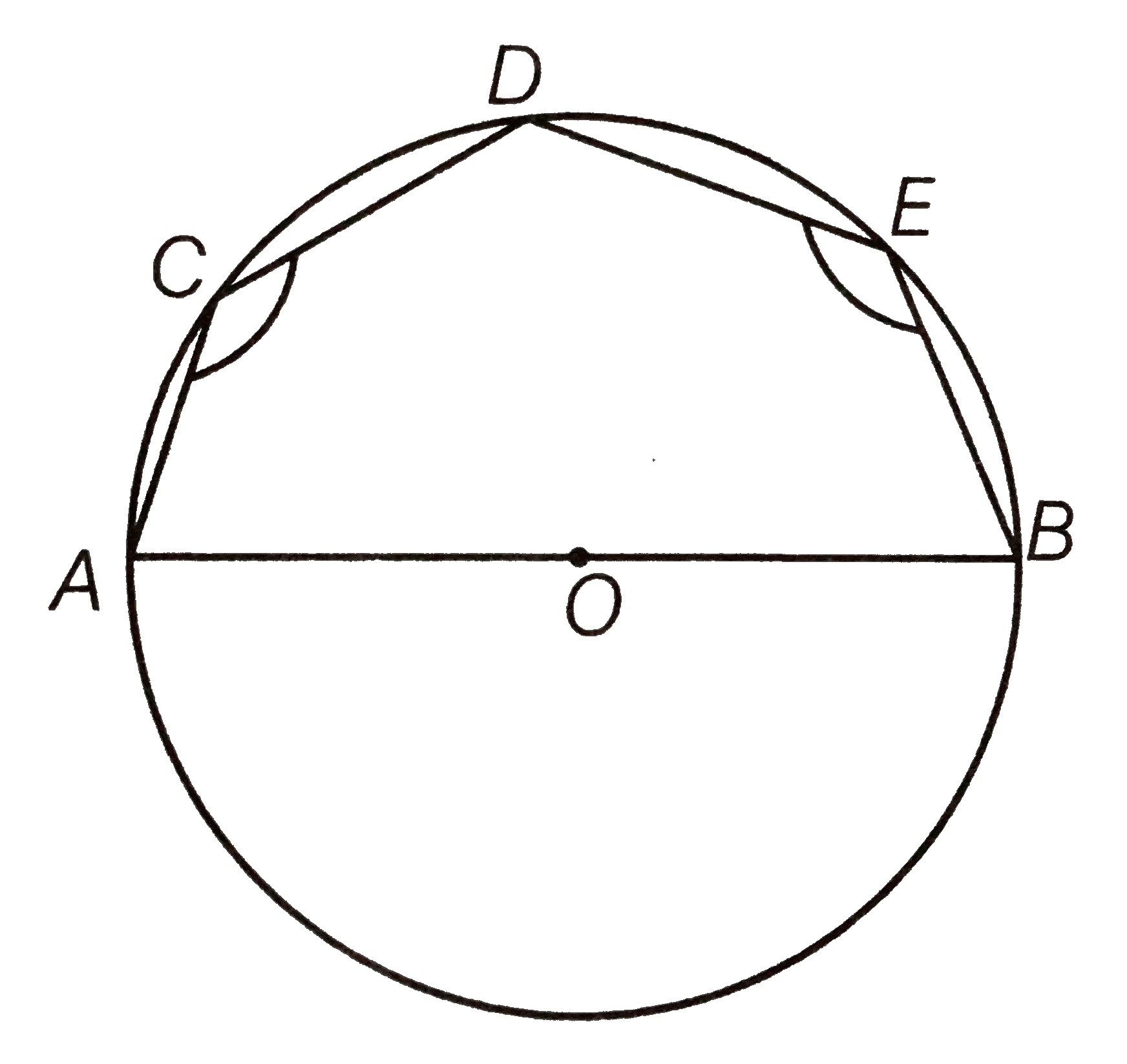
In figure, AOB is a diameter of the circle and C, D, E are any three points on the semi-circle. Find the value of ∠ACD+∠BED.
View SolutionProve that the points (6,4) (4,5) and (2,6) are collinear.
View SolutionThrough three collinear points a circle can be draw.
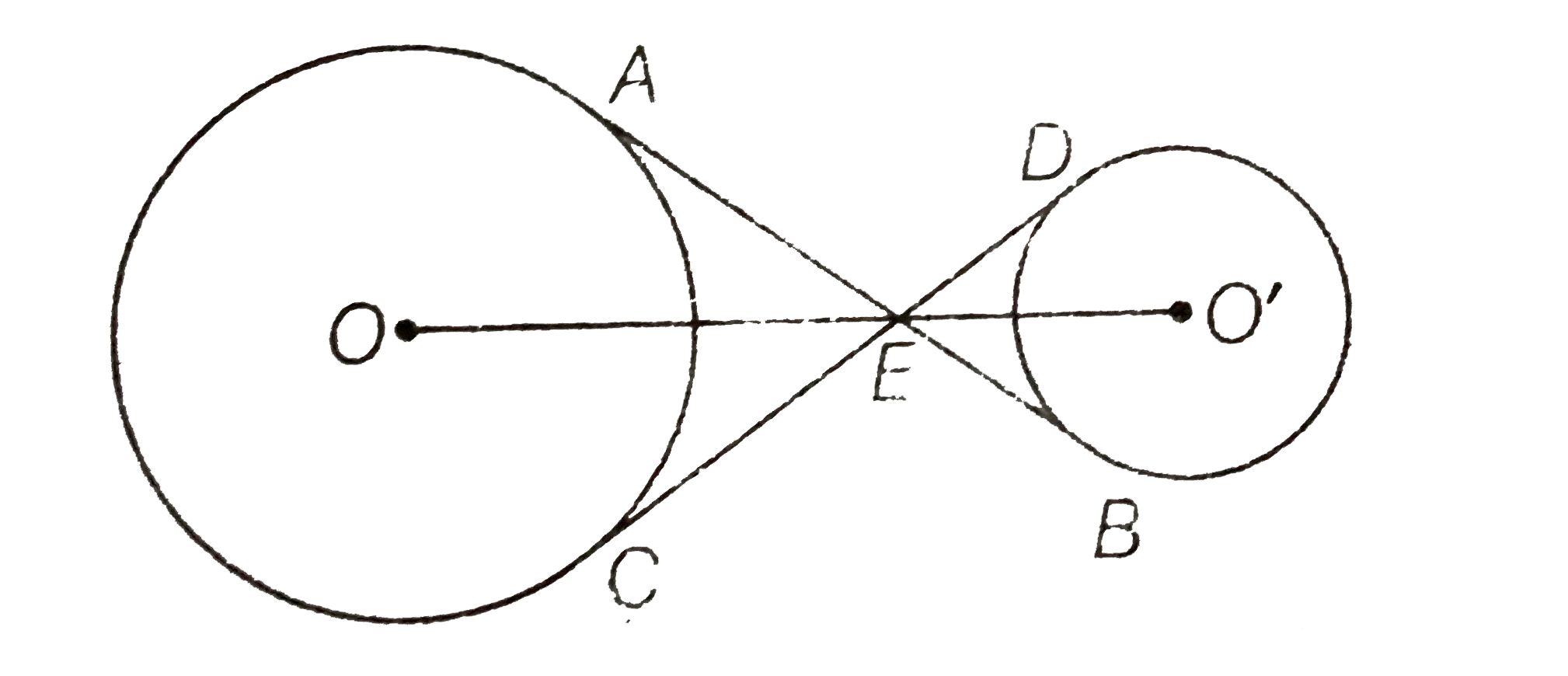
View SolutionThe common tangents AB and CD to two circles with centres O and O' intersect at E between the centres. Prove that the points O, E and O' are collinear.
View SolutionIn a figure the common tangents, AB and CD to two circles with centers O and O' intersect at E. Prove that the points O, E and O' are collinear.
View SolutionProve that the points (−2, 5), (0, 1) and (2, −3) are collinear.
View SolutionThere are 20 points in a plane. How different triangles can be formed with these points? (no three points are collinear).
View Solution
