In the figure, m(arc WY)=44∘,m(arc ZX)=68∘,then
If WT=4.8, TX=8.0, YT=6.4, find TZ.
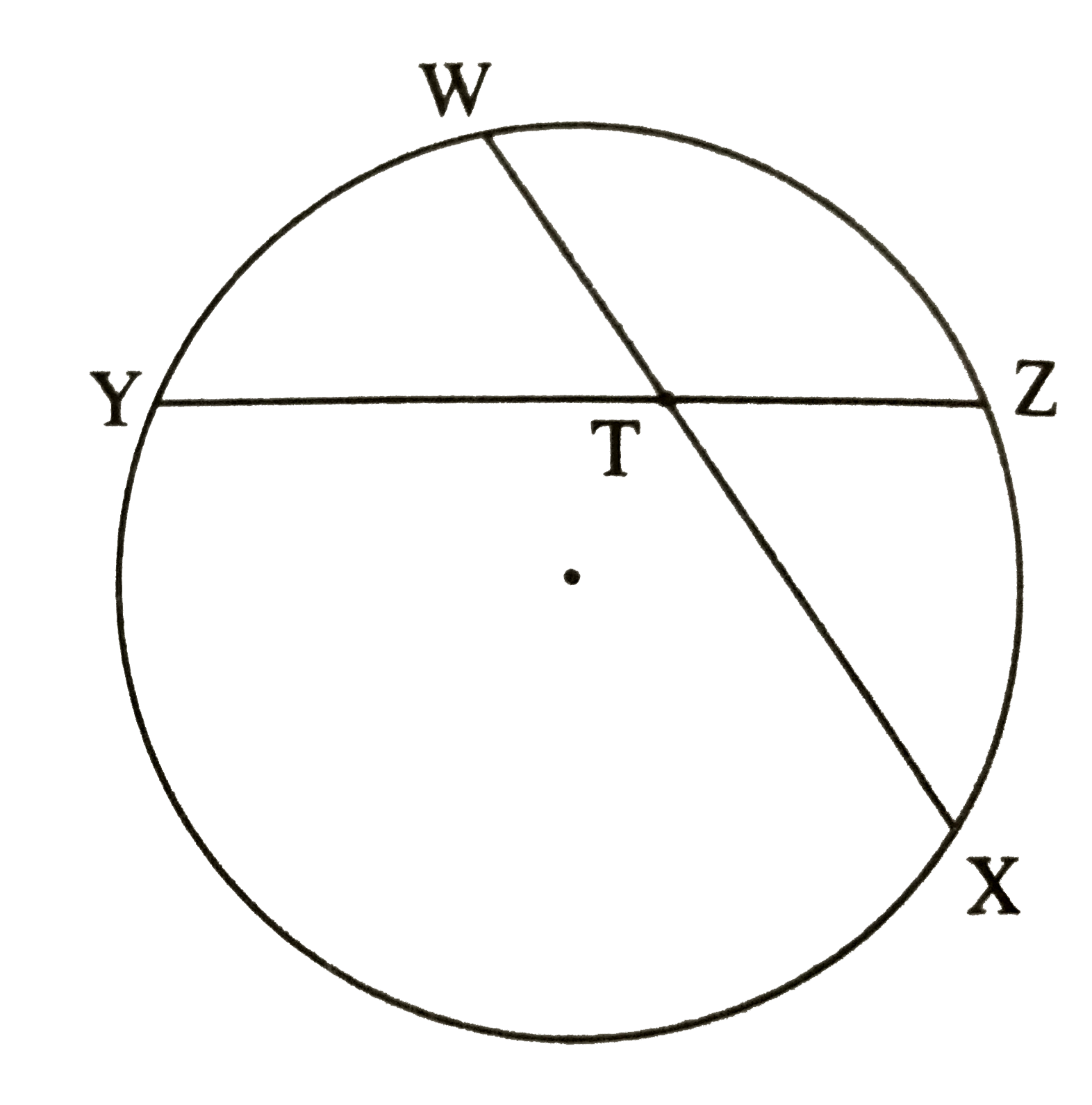
The correct Answer is:TZ=6
Step by step video & image solution for In the figure, m(arc WY)=44^(@),m(arc ZX)=68^(@),then If WT=4.8, TX=8.0, YT=6.4, find TZ. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - Challenging Questions
10 Videos
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - PRACTICE SET 3.5
6 Videos
- CHALLENGING QUESTIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve any one of the following subquestions :
1 Videos
- COORDINATE GEOMETRY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - COORDINATE GEOMETRY EXERCISE - Assignment 6.5
13 Videos
Similar Questions
In the figure, m(arc WY)=44∘,m(arc ZX)=68∘,then
If WX=25, YT=8, YZ=26, find WT.
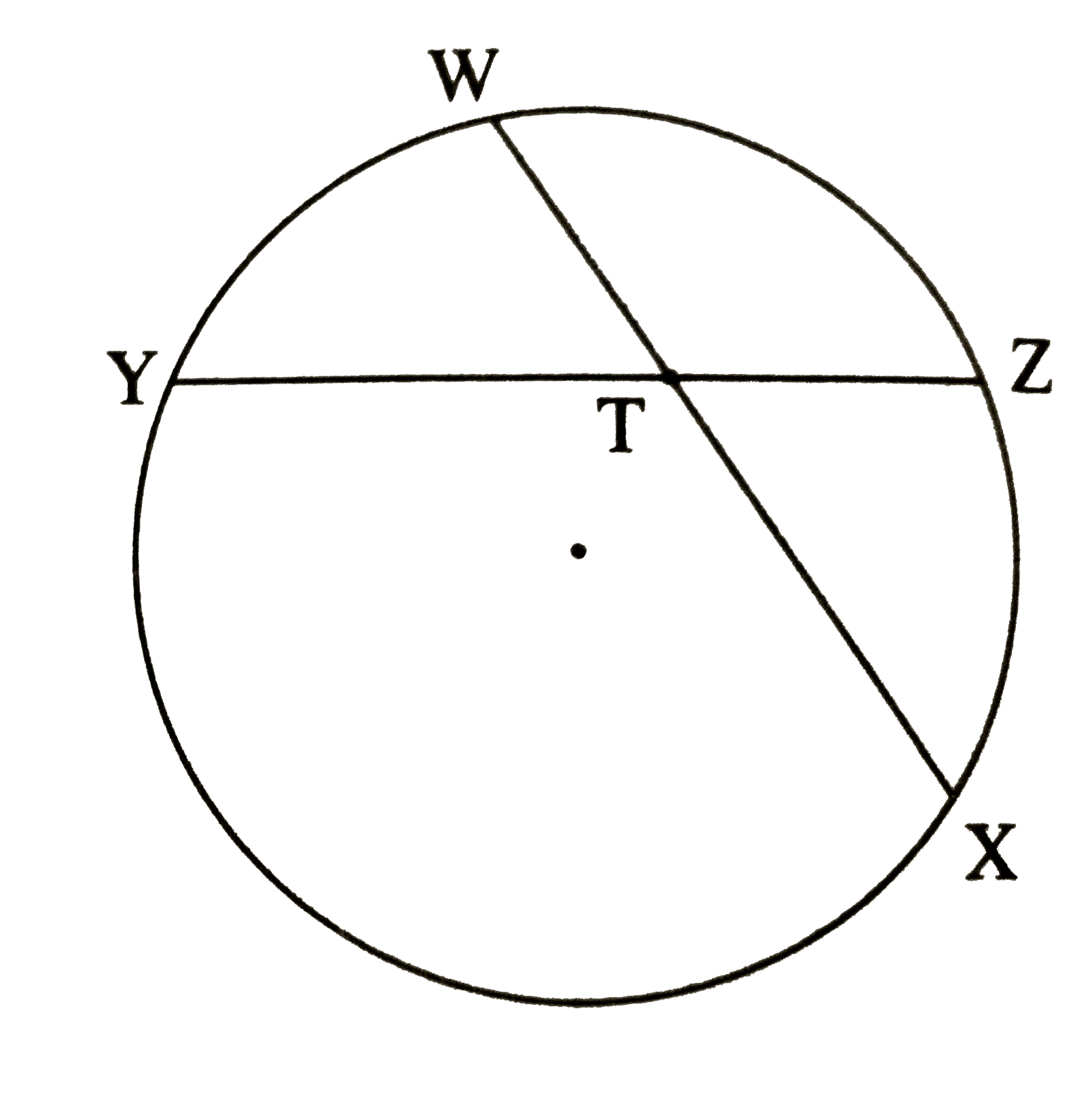
View SolutionIn the figure, m(arc WY)=44∘,m(arc ZX)=68∘,then
Find the measure of ∠ZTX.
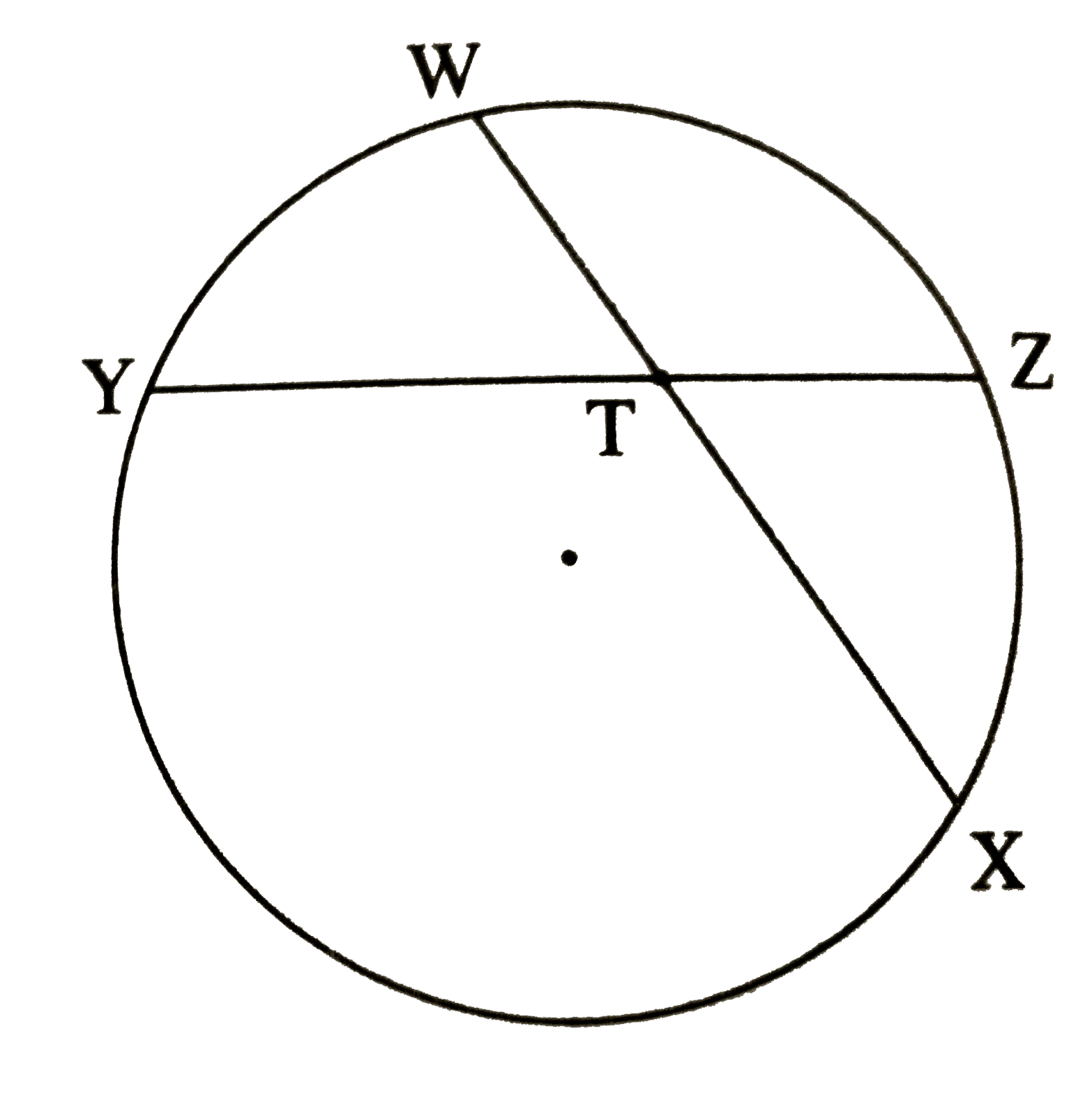
View SolutionIn the figure,
(1) m (arc CE ) =54∘, m (arc BD ) 23∘, find measure of ∠CAE .
(2) If AB = 4.2 , BC = 5.4 , AE = 12.0, find AD .
(3) If AB = 3.6, AC = 9.0 , AD = 5.4 , find AE.

View SolutionIn the figure,
m ) arc NS ) =125∘
m ( arc EF ) = 37∘
find the measure ∠NMS,

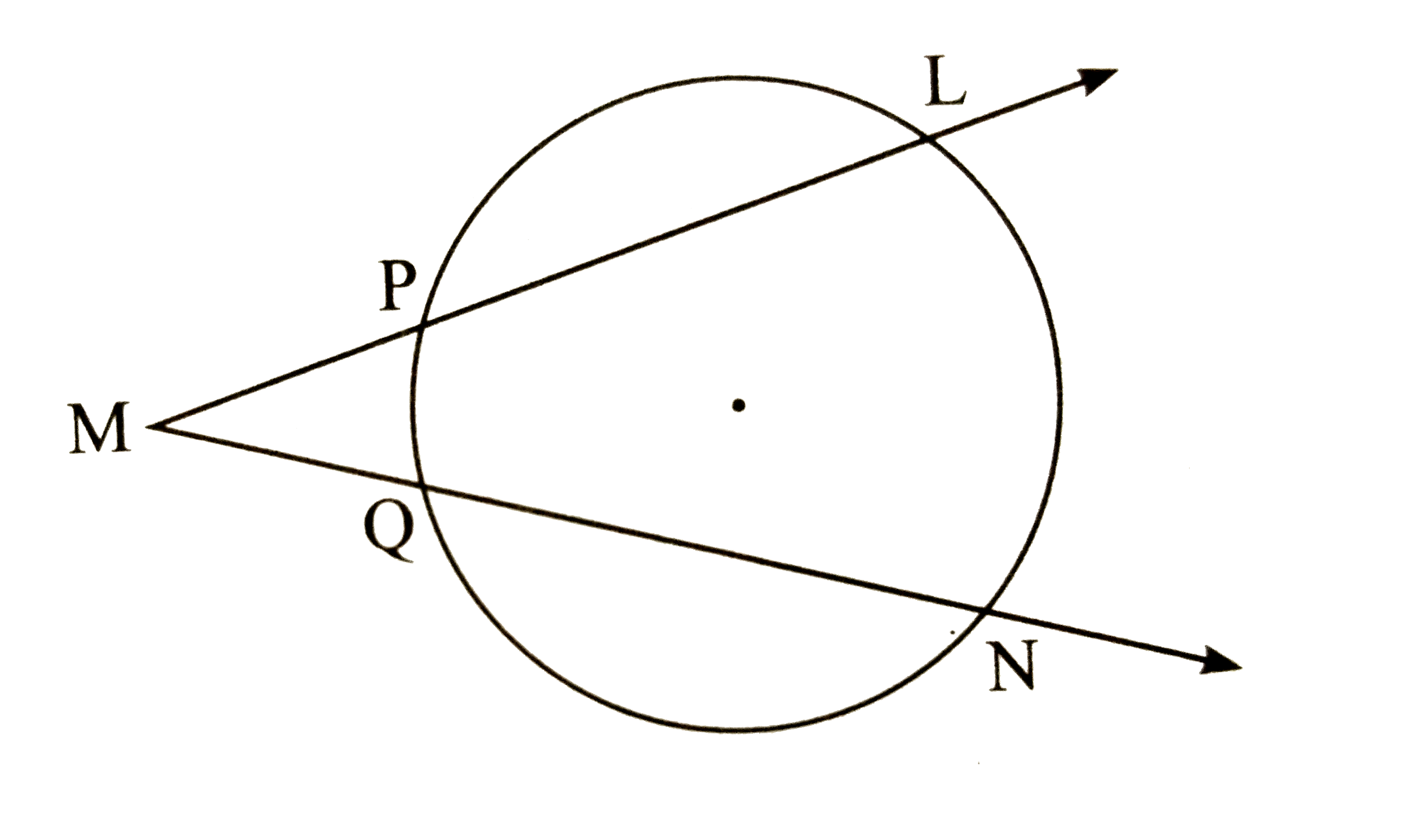
View SolutionIn the figure , if m ( arc DXE 0 =100∘ and m (arc AYC ) =40∘, find ∠DBE.

View SolutionIn the figure, m (arc LN ) =110∘, m ( ar PQ ) = 50∘ then complete the following activity to find ∠LMN
∠LMN=12[m(arcLN)=−□]
∴∠LMN=12[□−50∘]
∴_LMN=12×□
∴∠LMN=□
View SolutionIn the figure, m ( arc NS ) =130∘
m (arc EF ) =60∘. Find
(i) ∠NMS
(ii) ∠ENF
( iii) ∠NFS
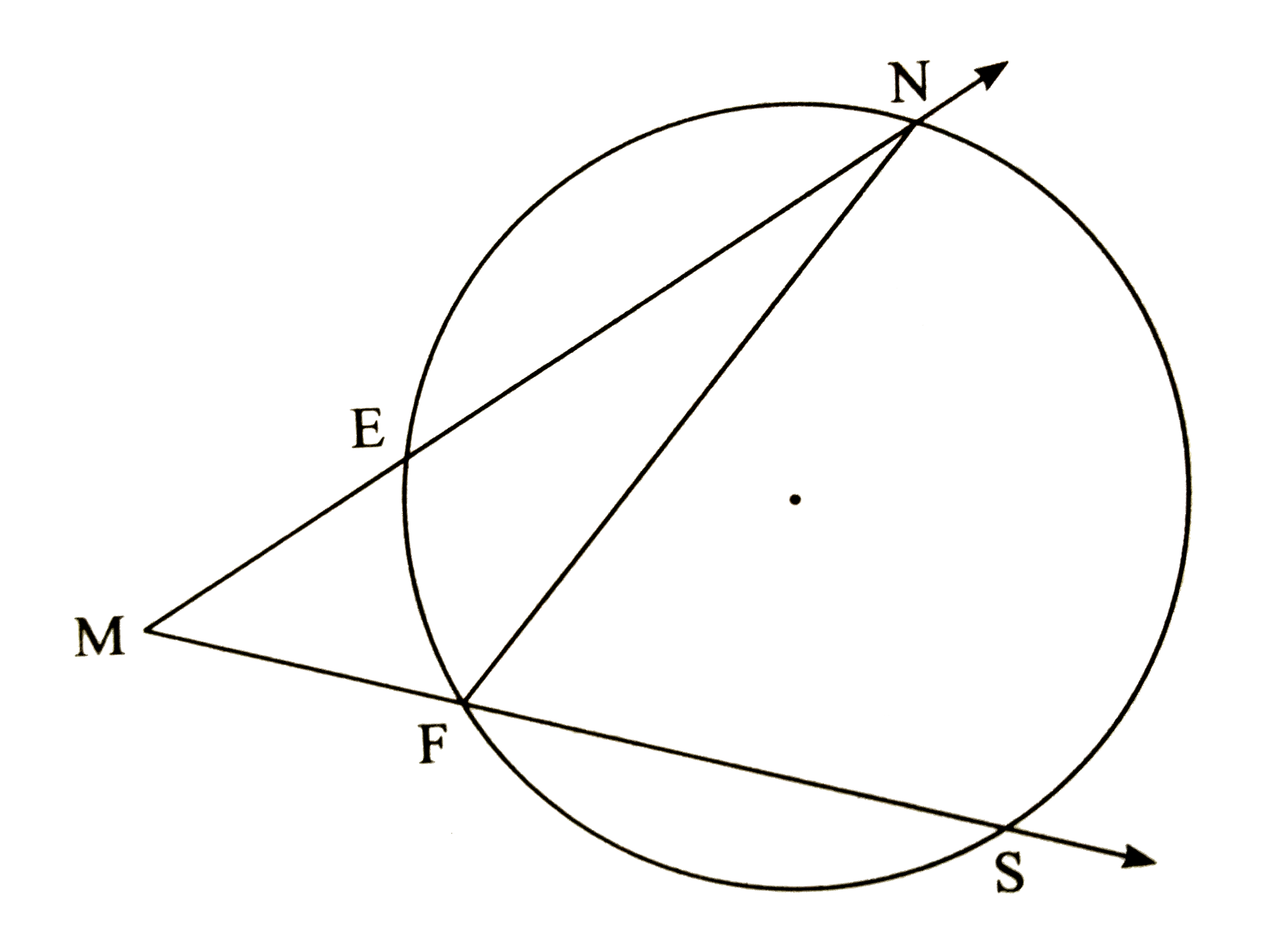
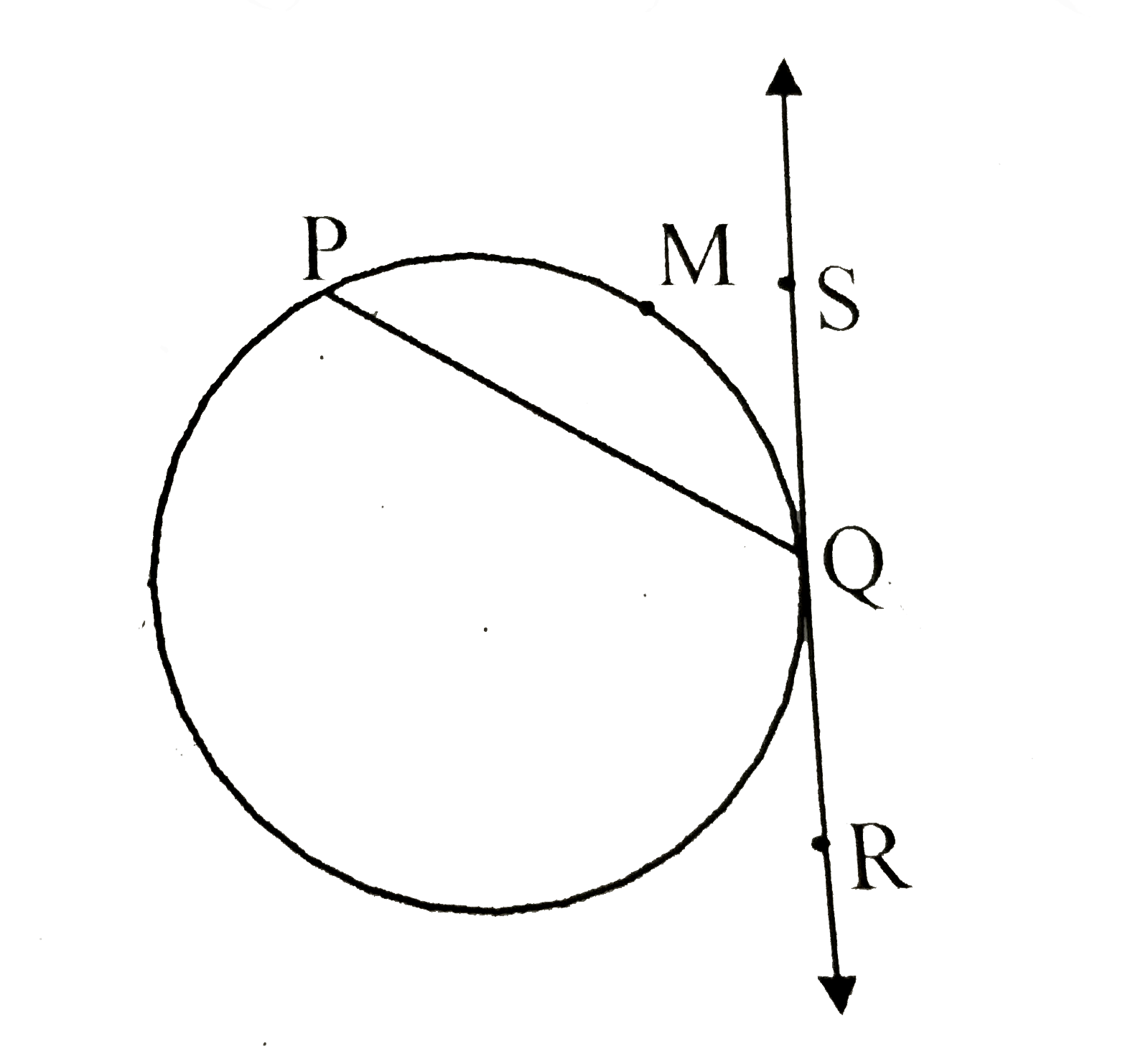
View SolutionIn the following figure, m(arc PMQ) =110∘, find ∠PQS.
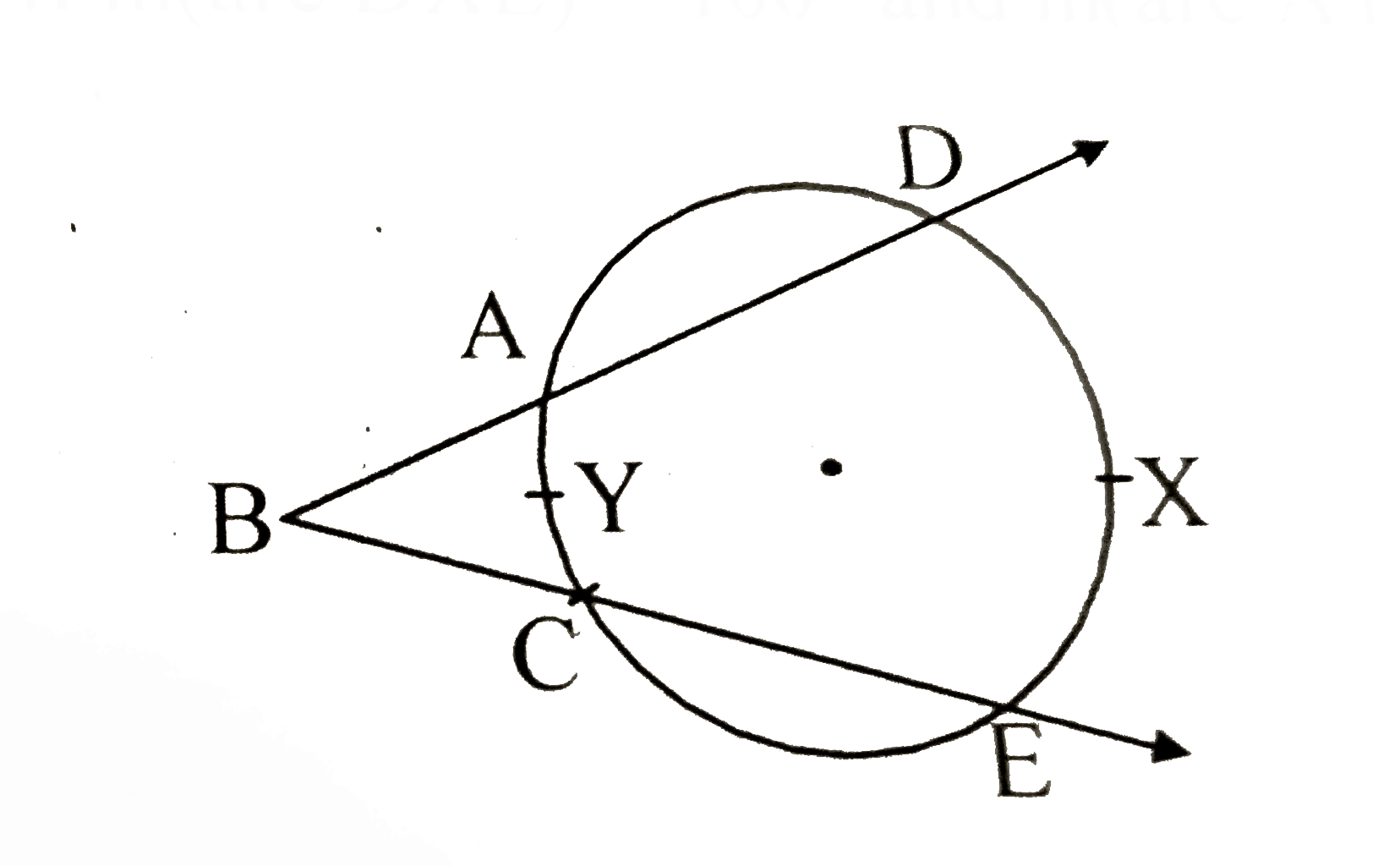
View SolutionIn the following figure, if m(arc DXE) =100∘ and m(arc AYC) =40∘, find ∠DBE.
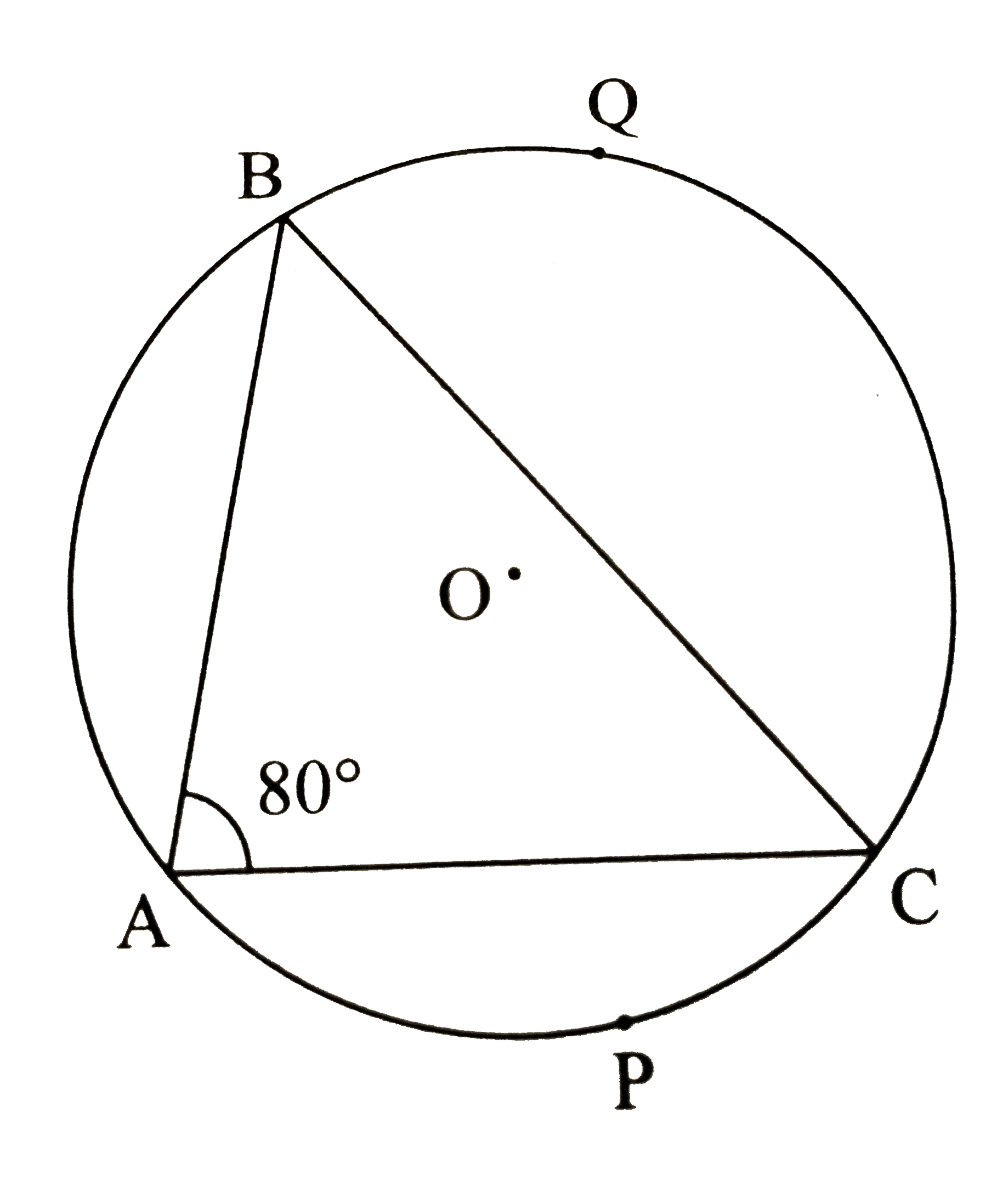
View SolutionIn the figure, O is the centre of the circle , ∠BAC=80∘, m ( arc APC ) =60∘ then find the measure of
(i) ∠ABC (ii) arc BQC
View Solution
