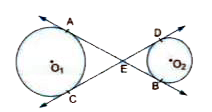
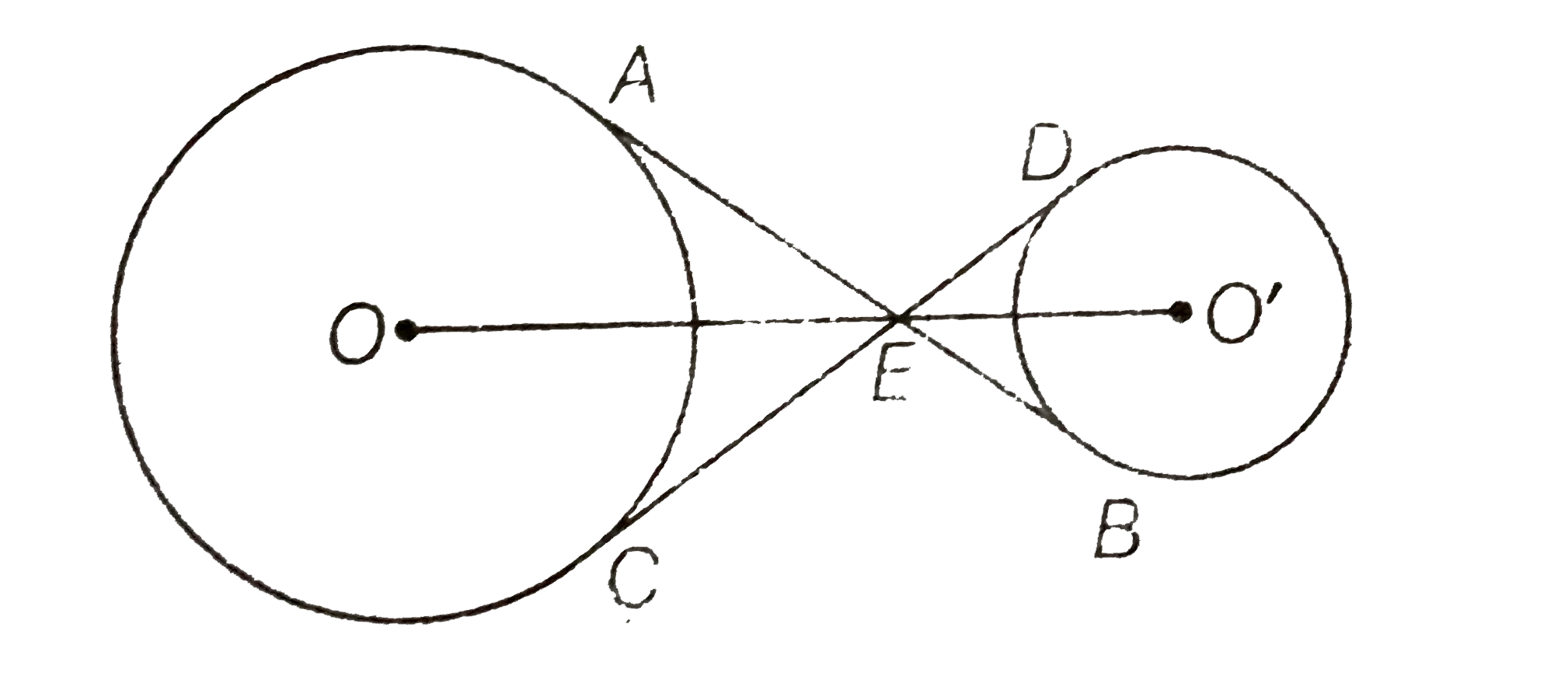
In a figure the common tangents, AB and CD to two circles with centers O and O' intersect at E. Prove that the points O, E and O' are collinear.
Video Solution
Text Solution
Joint AO, OC and O'D,O'B.
Now, in
O'D=O'B [radius] O'E=O'E [common side]
ED=EB
[since, tangents drawn from an external point to the circle are equal in length]
[by SSS congruence rule]
O'E is the angle bisector of
Similarly, OE is the angle bisector of
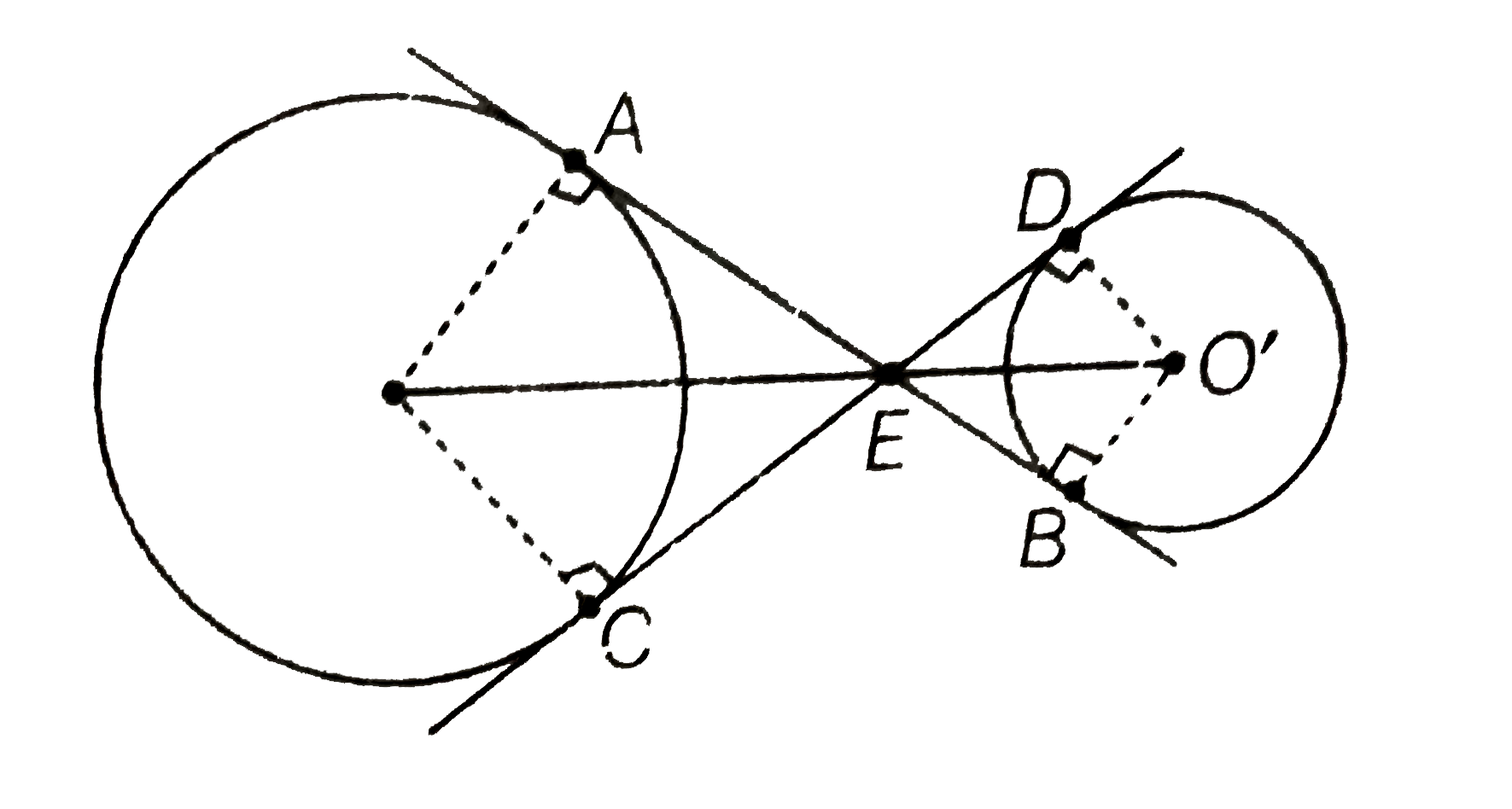
Now, in quadrilateral DEBO'.
[since, CED is a tangent to the circle and O'D is the radius, i.e., ]
[since, DEBO' is cyclic quadrilateral]......(ii)
Since, AB is a straight line.
Similarly,
Again from Eq. (ii),
Divided by 2 on both sides, we get
[since, O'E is the angle bisector of ]
Similary,
Divided by 2 on both sides, we get
[since, OE is the angle bisector of ]
Now,
[from Eqs. (iii) and (iv)]
So, OEO' is straight line.
Hence, O, E and O' are collinear. Hence proved.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Two chords AB and CD of a circle with centre O intersect at point P within the circle. ∠AOC+∠BOD=?
A∠APCB2∠APCC32∠APCDNone of these
In figure, common tangents AB and CD to two circles intersect at E. Prove that AB=CD.

View SolutionCommon tangents AB and CD to two circles intersects at E. Prove that AB=CD
View SolutionIn the adjoining figure, common tangents AB and CD to two circles intersect at P.
Prove that AB=CD.

View SolutionIn the figure, two equal chords AB and CD of a circle with centre O, intersect each other at E, Prove that AD=CB
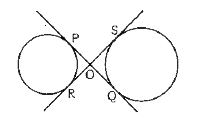
View SolutionIn the figure, PQ and RS are the common tangents to two circles intersecting at O.
Prove that PQ=RS
View SolutionIn Figure, two tangents ABandAC are drawn to a circle with centre O such that ∠BAC=1200. Prove that OA=2AB
View SolutionIn the figure,tangents at B and C of the circle with centre O intersect at point A. If ∠BAC=90∘ then prove □BACO is a square
View Solution