In the figure, P is the point of contact.
If m(arc PR)=140∘, ∠POR=36∘, find m(arc PQ).

The correct Answer is:m(arc PQ)=68∘
Step by step video & image solution for In the figure, P is the point of contact. If m(arc PR)=140∘, ∠POR=36∘, find m(arc PQ). by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - Challenging Questions
10 Videos
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - PRACTICE SET 3.5
6 Videos
- CHALLENGING QUESTIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve any one of the following subquestions :
1 Videos
- COORDINATE GEOMETRY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - COORDINATE GEOMETRY EXERCISE - Assignment 6.5
13 Videos
Similar Questions
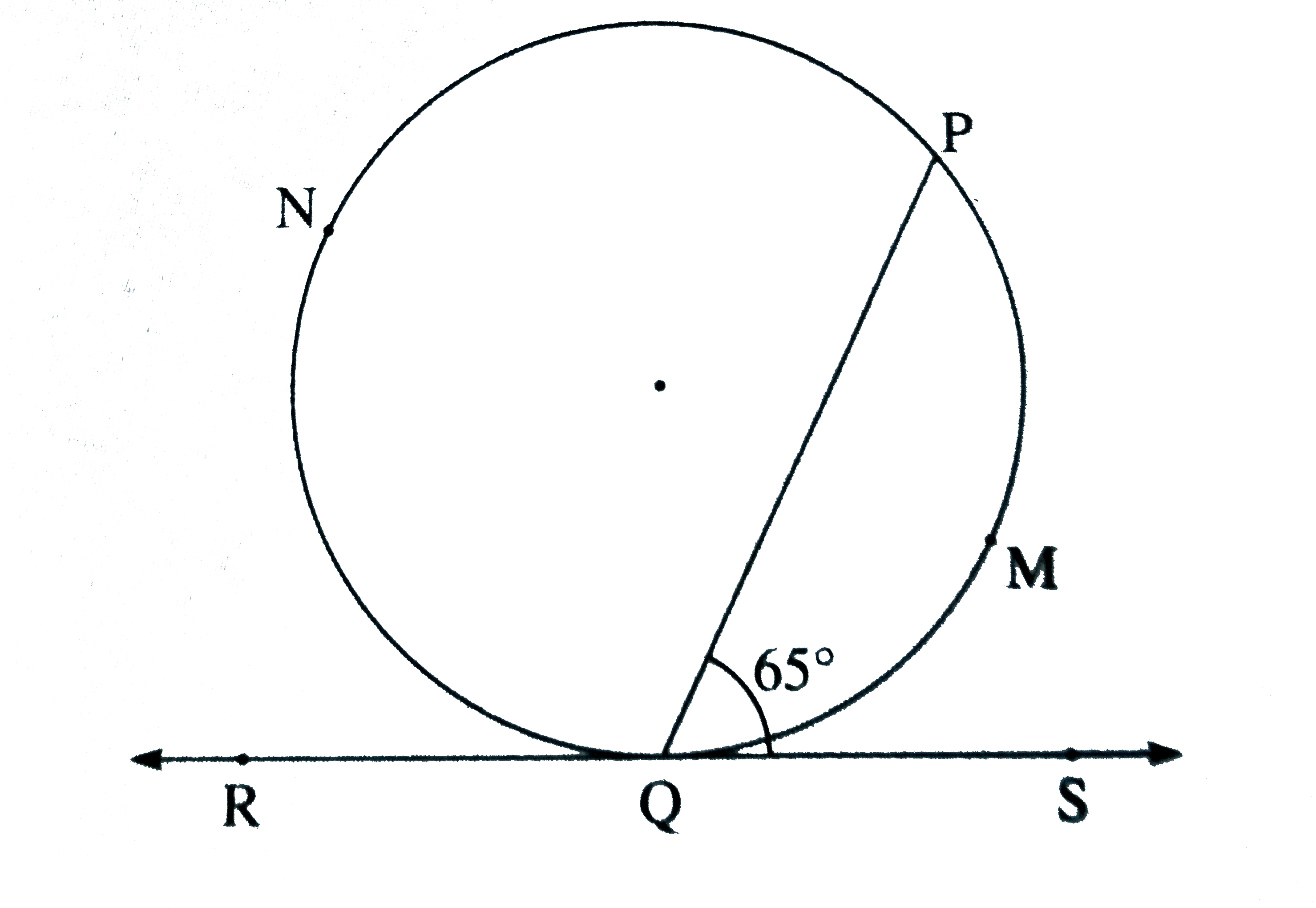
In the figure, line RS is tangent at point Q. If ∠PQS=65∘ find m(arc PMQ) and m(arc PNQ ).
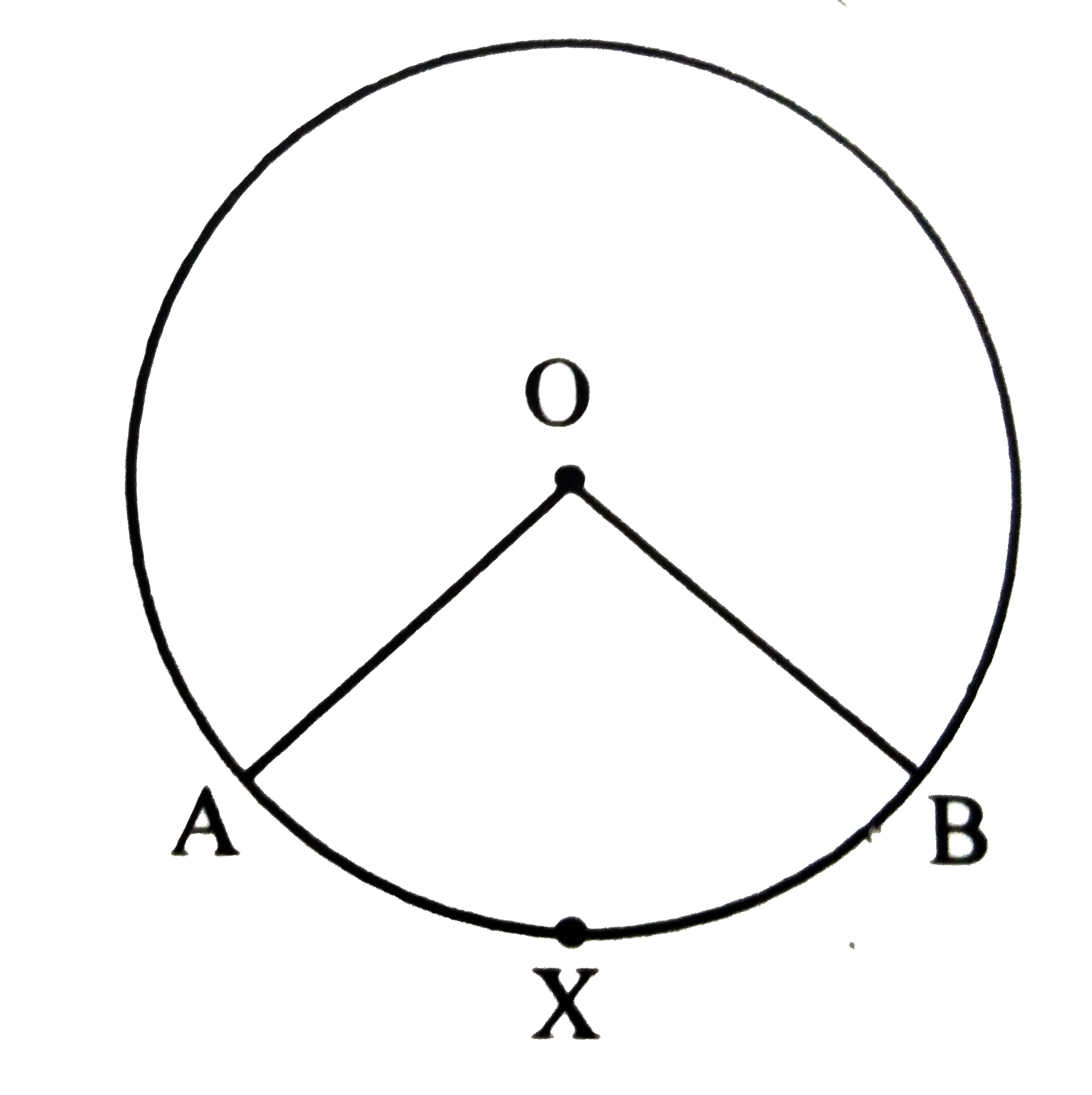
View SolutionIn the given figure , O is the centre of the circle. If m(arc AXB)=80∘, then m∠AOB=
View SolutionIn the figure, ray PQ touches the circle at point Q. If PQ =12, PR = 8, then find PS.

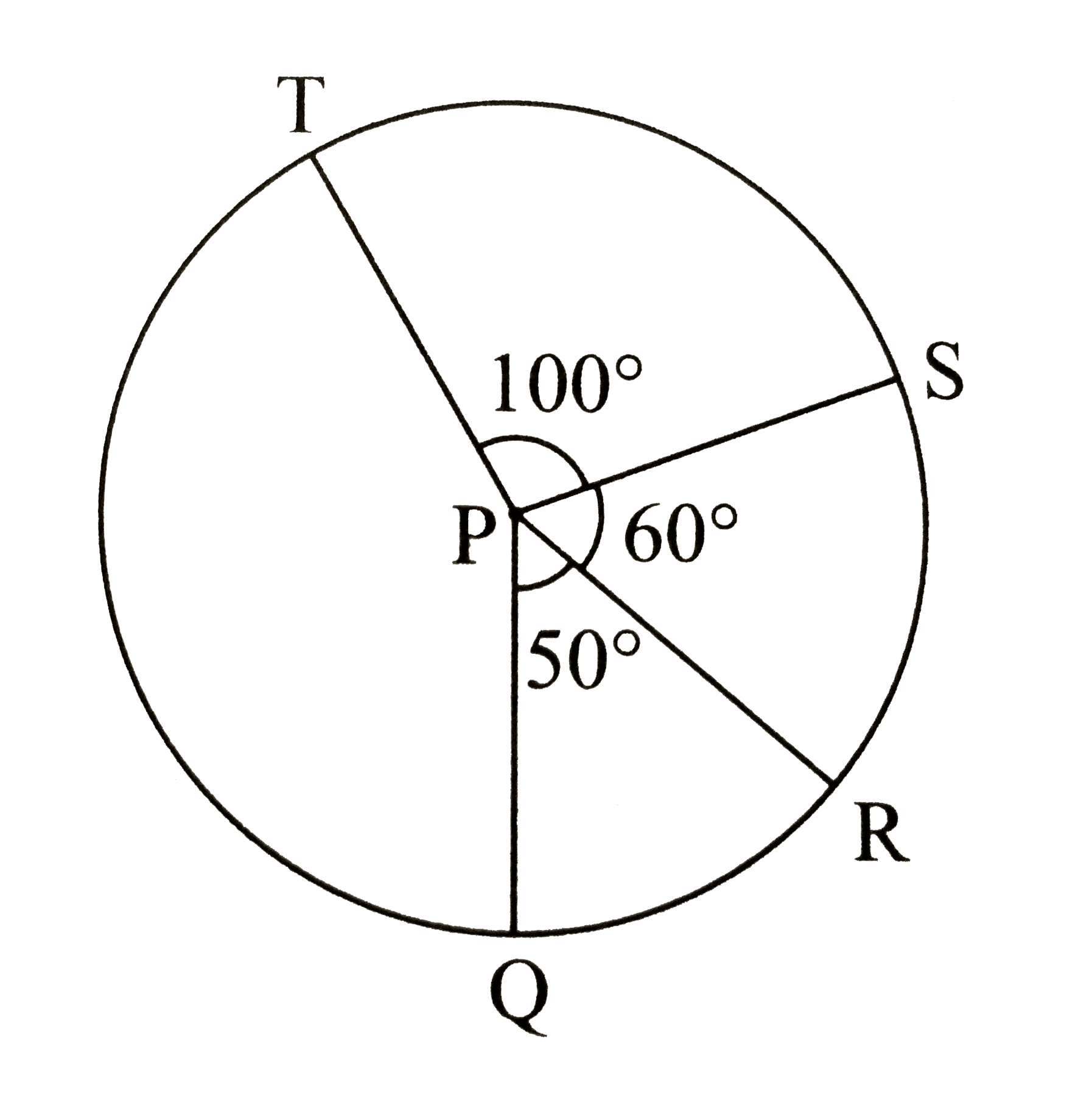
View SolutionIn the figure, P is the cnetre of the circle. If ∠QPR50∘,∠RPS=60∘,∠SPT=100∘ then find
(1) m(arc QRS) (ii) m ( arc QST ) (iii) m (arc RTS )
View SolutionIn the figure, seg AB is the diameter of the circle, ∠ABC=30∘, Find (1) m(arc AXC)
(2) m(arc BYC)

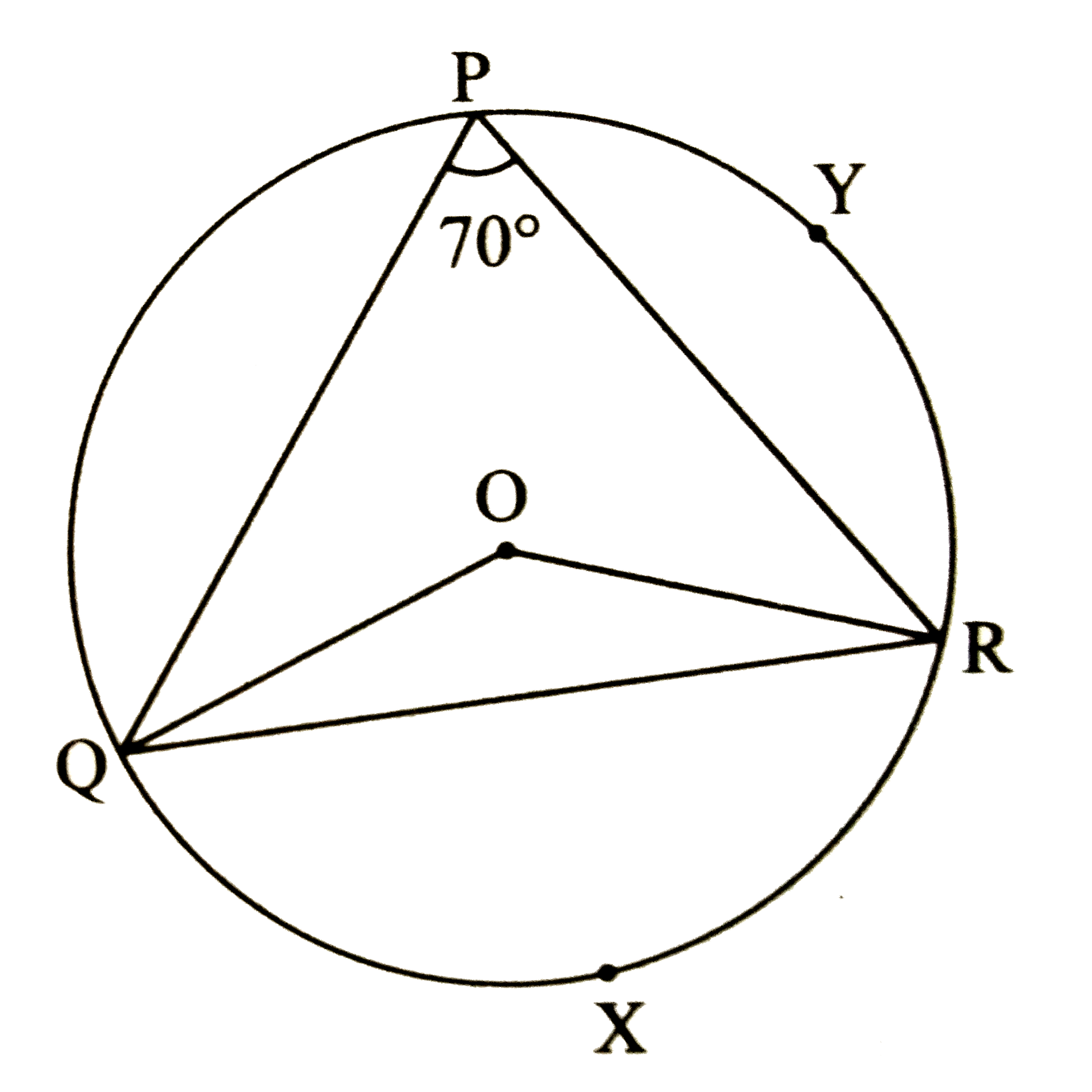
View SolutionIn the figure, O is the centre of circle ∠QPR=70∘ and m (arc PYR ) =160∘, then find the value of each of the following :
(a) m ( arc QXR )
(b) ∠QOR
(c ) ∠PQR
View SolutionIn the figure, □PQRS is cyclic side PQ ≅ RQ, ∠PSR=110∘, Find
m(arc PQR)
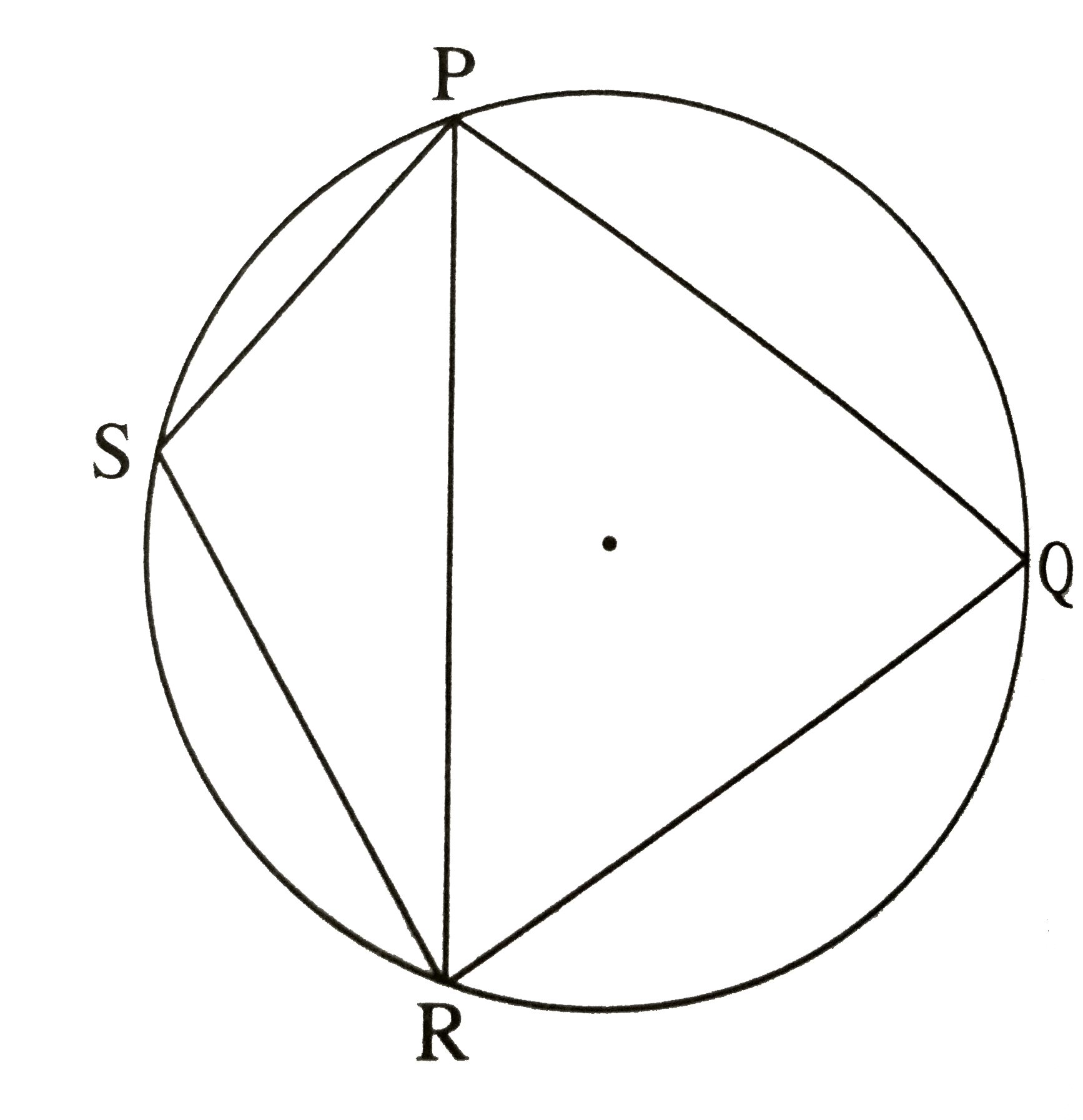
View SolutionIn the figure, □PQRS is cyclic side PQ ≅ RQ, ∠PSR=110∘, Find
m(arc QR)

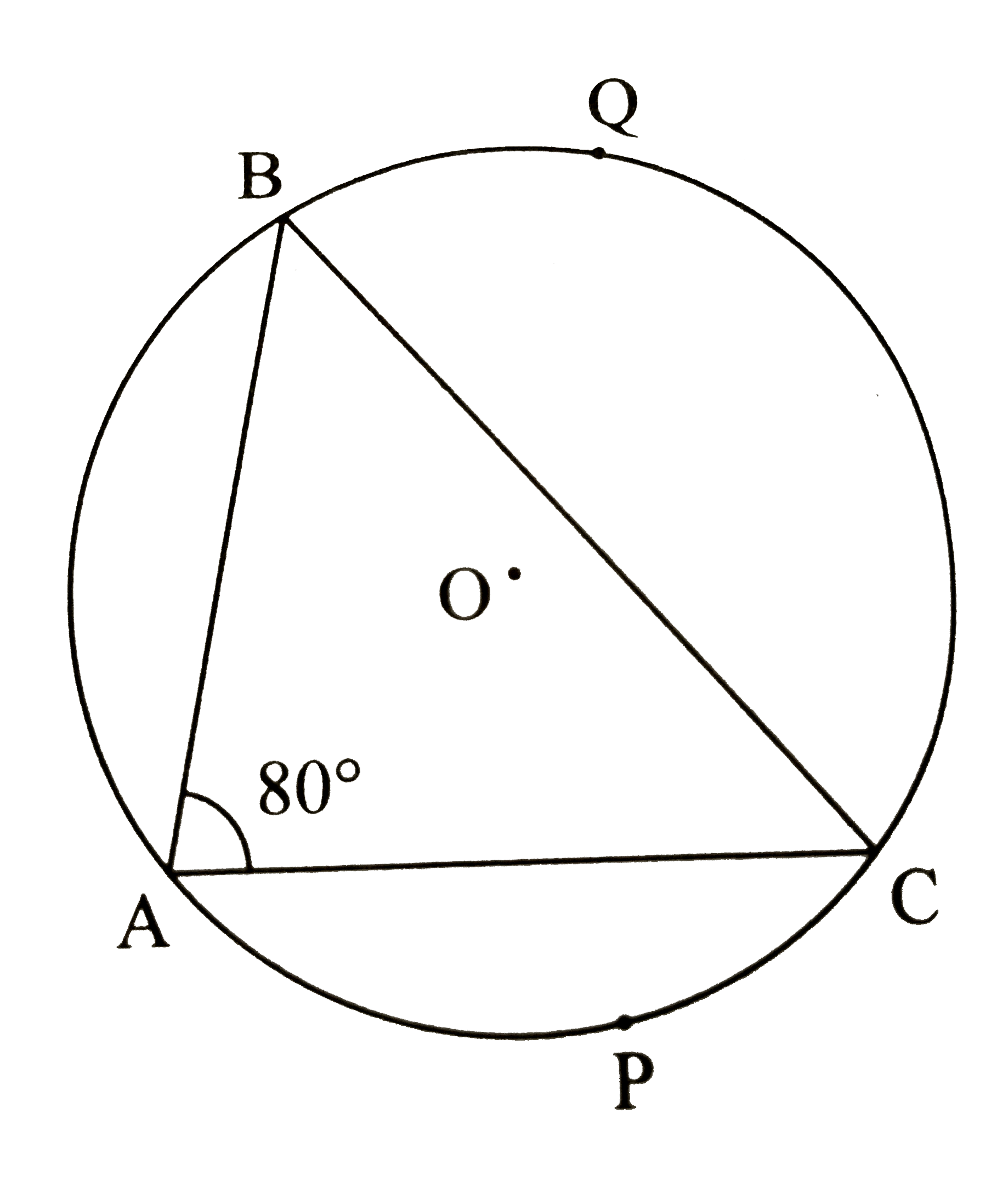
View SolutionIn the figure, O is the centre of the circle , ∠BAC=80∘, m ( arc APC ) =60∘ then find the measure of
(i) ∠ABC (ii) arc BQC
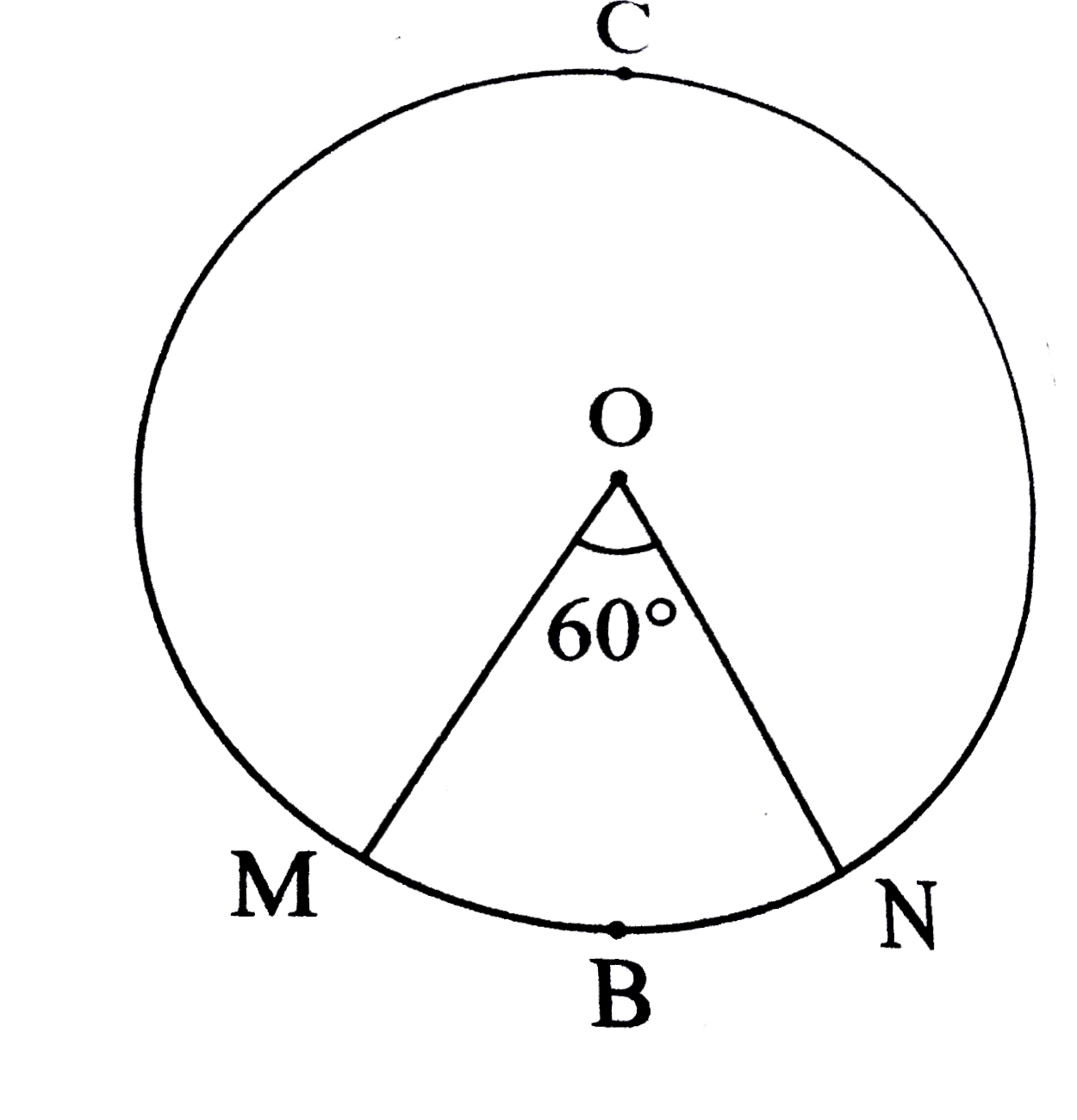
View SolutionIn the figure, radius of the circle is 7 cm and m(arc MBN) =60∘, find
(1) Area of the circle.
(2) A(O-MBN).
(3) A(O-MCN).
View Solution
