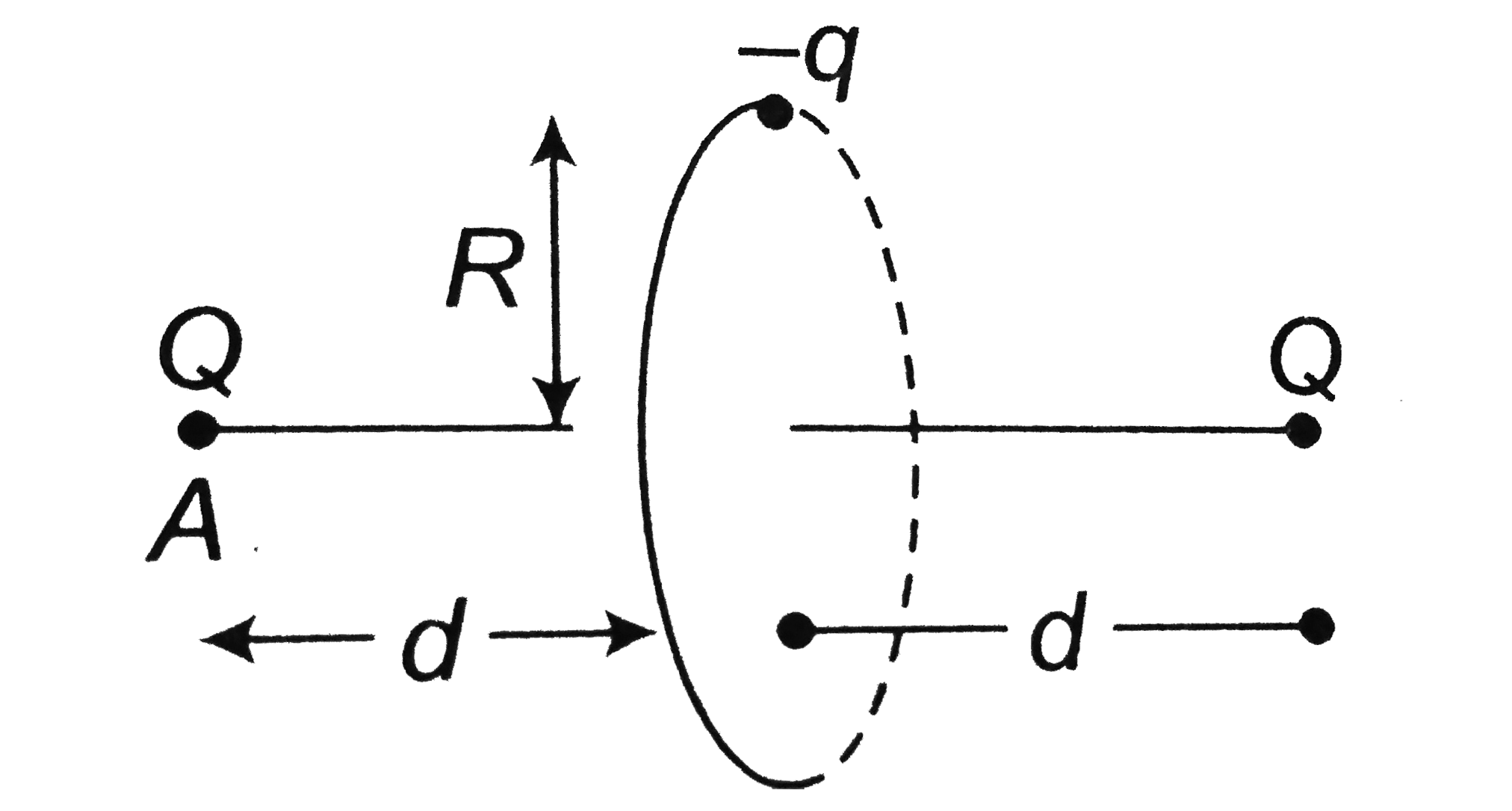
Two positive point charges each of magnitude 10C are fixed at positions A &B at a seperation 2d=6m. A negatively charged particle of mass m=90gm and charge of magnitude 10×10−6C is revolving in a circular path of radius 4m in the plane perpendicular to the line AB and bisecting the line AB. Neglect the effect of gravity. Find the angular velocity of the particle
200rad/s
400rad/s
250rad/s
100rad/s
The correct Answer is:b
Net force on −q towards the centre,

F=(2F1.sinθ)
=2.KQ.qd2+d2×R√d2+d2
For parctice to move in circle
F=mω2R
⇒2KQqr(d2+R2)mω2R
⇒ω=
⎷2KQqm(d2+R2)3/2
=
⎷2×9×109×10×10×10−690×10−3×(32+42)3/2=400rad/s
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Section B - Assertion Reasoning25videos
ELECTRIC CHARGE, FIELD & FLUX
- BOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - AIPMTNEET Questions24videos
ELECTRIC CHARGE, FIELD & FLUX
- BOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Electric Dipole29videos
ELECTRIC CHARGE, FIELD & FLUX
- BOOK - A2ZCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Section D - Chapter End Test30videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Section D - Chapter End Test29videos
ELECTRIC POTENTIAL & CAPACITANCE
Similar Questions
A particle of charge q1 and mass m is revolving around a fixed negative charge of magnitude q2 in a circular path of radius r. Find the time period of revolution.
View SolutionA particle of mass m carrying charge '+q1' is revolving around a fixed charge '−q2' in a circular path of radius r. Calculate the period of revolution.
View Solution
Knowledge Check
- Question 1 - Select One
Consider two positive point charges, each of magnitude q, placed on the y-axis at the points (0, a) and (0, -a). A positively charged particle of charge q' and mass m is displaced slightly from the origin in the direction of the positive x-axis.
Speed of charge q' at infinity isA√qq'πε0mB√q'πε0amC√qq'ε0amD√qq'πε0am - Question 2 - Select One
Consider two positive point charges, each of magnitude q, placed on the y-axis at the points (0, a) and (0, -a). A positively charged particle of charge q' and mass m is displaced slightly from the origin in the direction of the positive x-axis.
At the origin, charge q' will be inAstable equilibriumBunstable equilibriumCneutral equilibriumDcannot determine - Question 3 - Select One
Consider two positive point charges, each of magnitude q, placed on the y-axis at the points (0, a) and (0, -a). A positively charged particle of charge q' and mass m is displaced slightly from the origin in the direction of the positive x-axis.
At the origin, charge q' will be inA B
B C
C D
D
A positive charge 'Q' is fixed at a point A negatively charged particle of mass ' 'm' and charge 'q' is revolving in a circular path of radius r1 ,with Q' as the centre.The change in potential energy to change the radius of the circular path from r1 to r2 in joule is
View SolutionA particle of mass m carrying a charge −q1 starts moving around a fixed charge +q2 along a circulare path of radius r. Find the time period of revolution T of charge −q1.
View SolutionA uniformly charged (linear charge density a) very long wire in placed fixed. A negative charge particle - of mass m revolves around this wire in a circular path of radius then +++++++ m
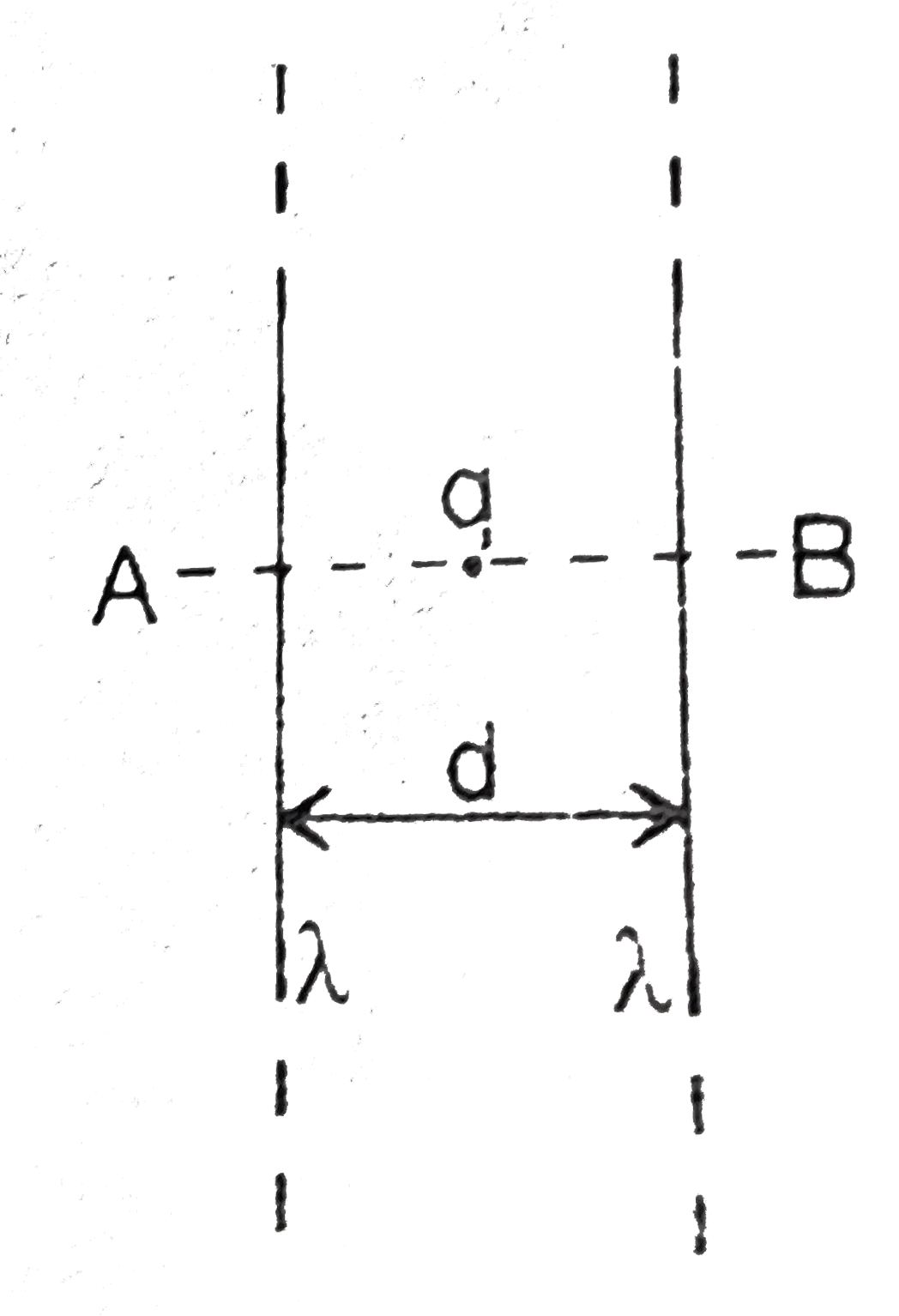
View SolutionTwo infinitely long line charges having charge density λ each are parallel to each other and separated by distance d. A charge particle of mass m and charge q is placed at mid point between them. This charge displaced slightly along a line AB which is perpendicular to the line charges and in the plane of the charges. prove that the motion of the particle will be SHM for small displacement and λq>0 Neglect gravity. Find the time period.
 View Solution
View SolutionTwo identical charges, 5μC each are fixed at a distance 8 cm and a charged particle of mass 9×10−6kg and charge −10μC is placed at a distance 5 cm from each of them and is released. Find the speed of the particle when it is nearest to the two charges.
View Solution

