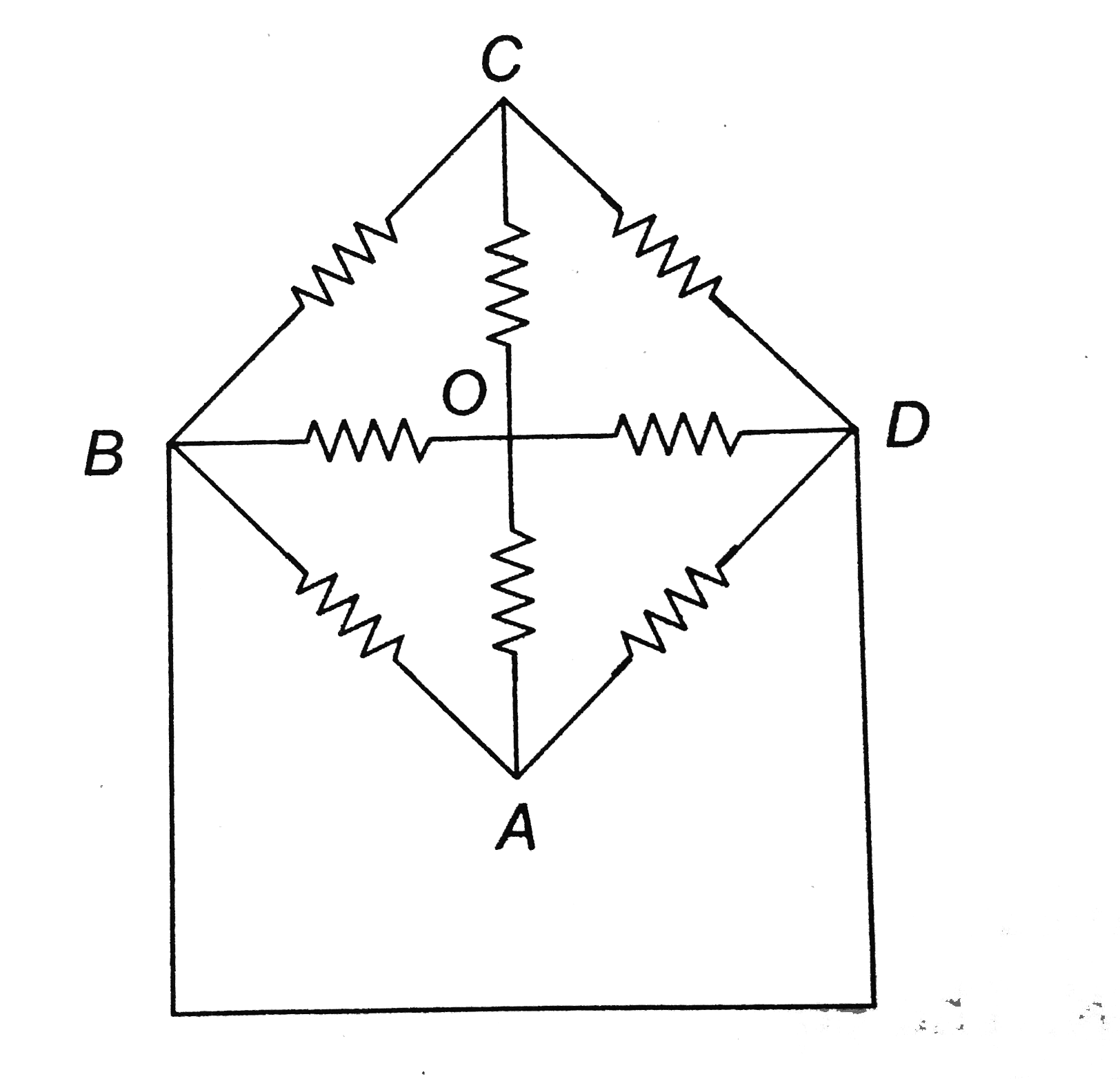
In the arrangement shown, the magnitude of each resistance is 2Ω. The equivalent resistance between O and A is given by
A
1415Ω
B
715Ω
C
43Ω
D
56Ω
Video Solution
Text Solution
The correct Answer is:A
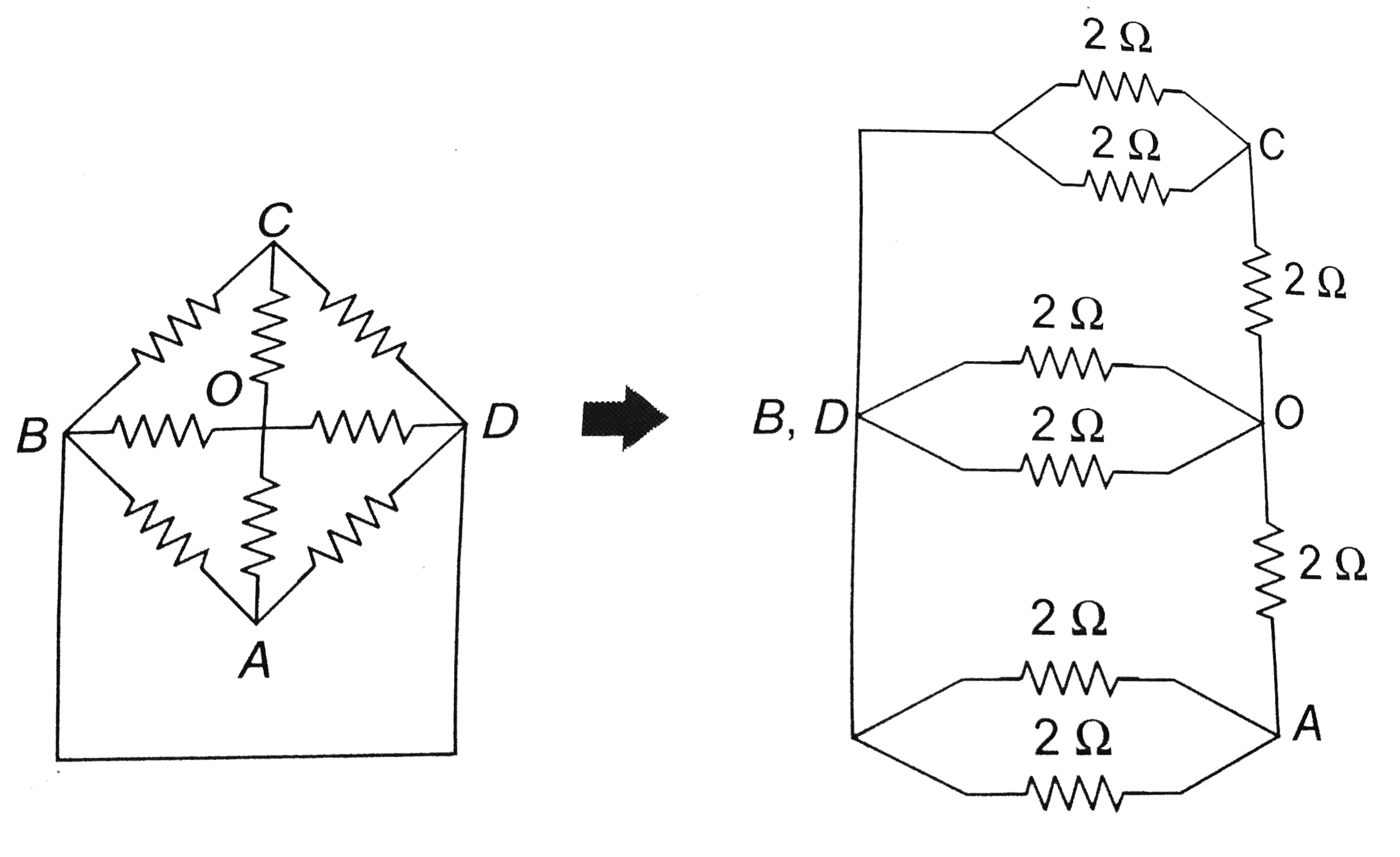
(a) Since magnitude of each resistance 2Ω the point B and D are equipotential
⇒VB−VD
Therefore we can connect these points with a conducting wire.
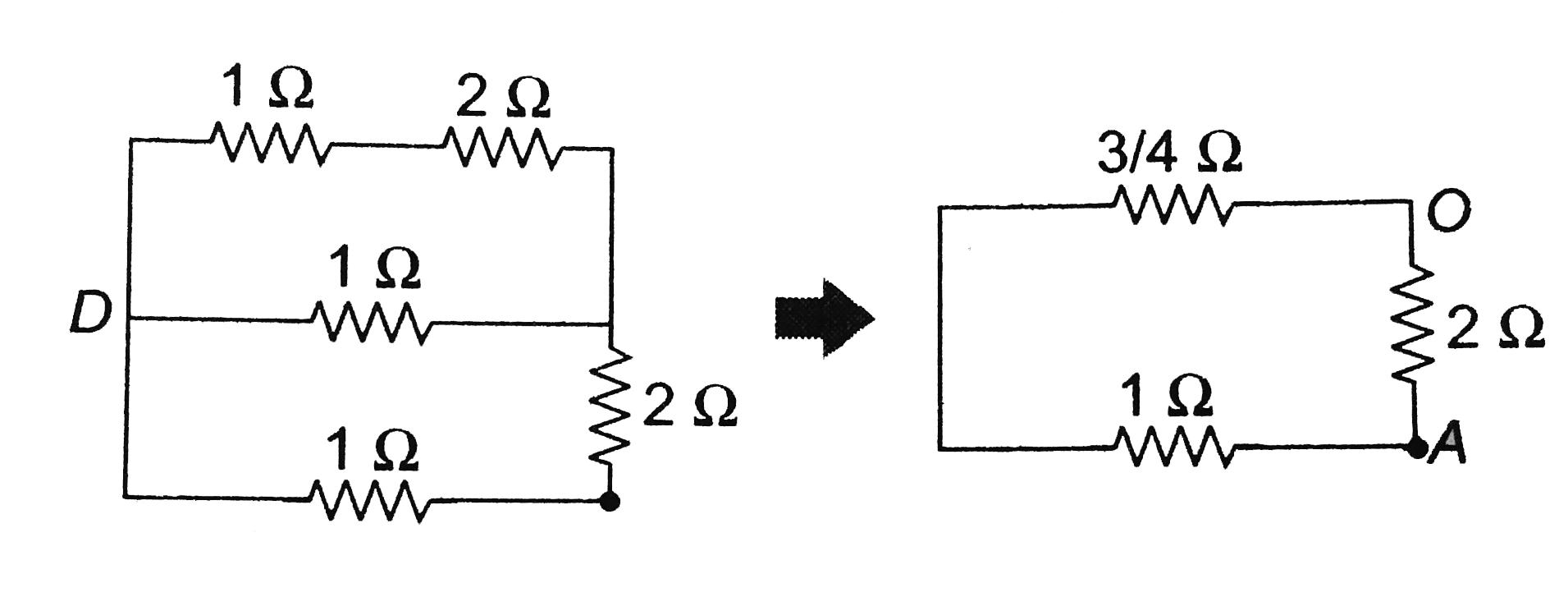
Req=(34+1)∣∣2=74×274+2=7×247+84
Req=1415Ω
|
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:A2ZChapter:CURRENT ELECTRICITYExercise:Kircoff'S Laws And Simple Circuits
Explore 64 Videos
- CURRENT ELECTRICITYBook:A2ZChapter:CURRENT ELECTRICITYExercise:R-C Circuits
Explore 17 Videos
- CURRENT ELECTRICITYBook:A2ZChapter:CURRENT ELECTRICITYExercise:Section D - Chapter End Test
Explore 29 Videos
- ATOMIC PHYSICSBook:A2ZChapter:ATOMIC PHYSICSExercise:Section D - Chapter End Test
Explore 30 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:A2ZChapter:DUAL NATURE OF RADIATION AND MATTERExercise:Section D - Chapter End Test
Explore 30 Videos
Similar Questions
Knowledge Check
In the arrangement shown, the magnitude of each resistance is 1Ω. The equivalent resistance between O and A is given by
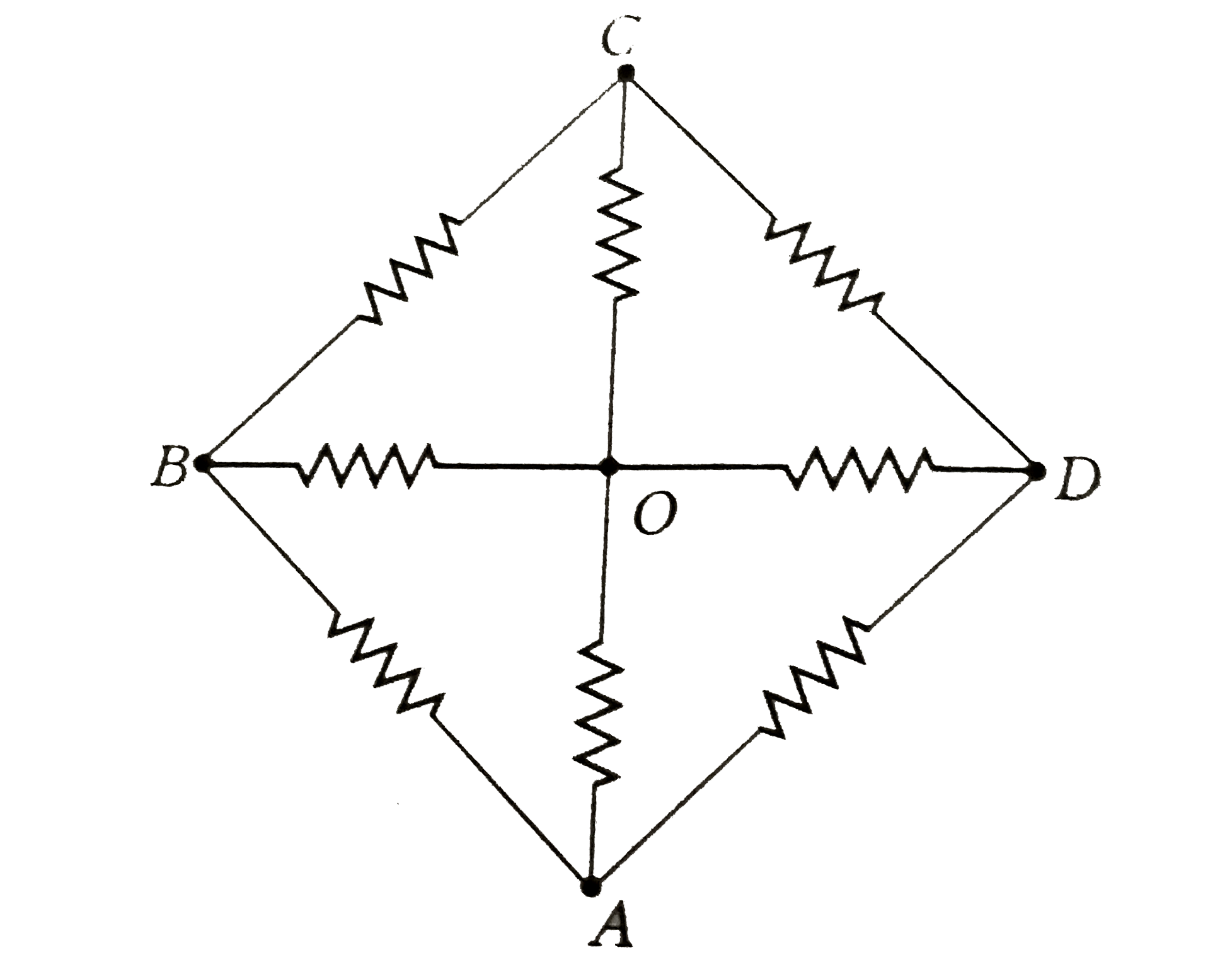 A1413ΩB34ΩC23ΩD56Ω
A1413ΩB34ΩC23ΩD56ΩEach resistance shown in figure is 2Ω. The equivalent resistance between A and B is
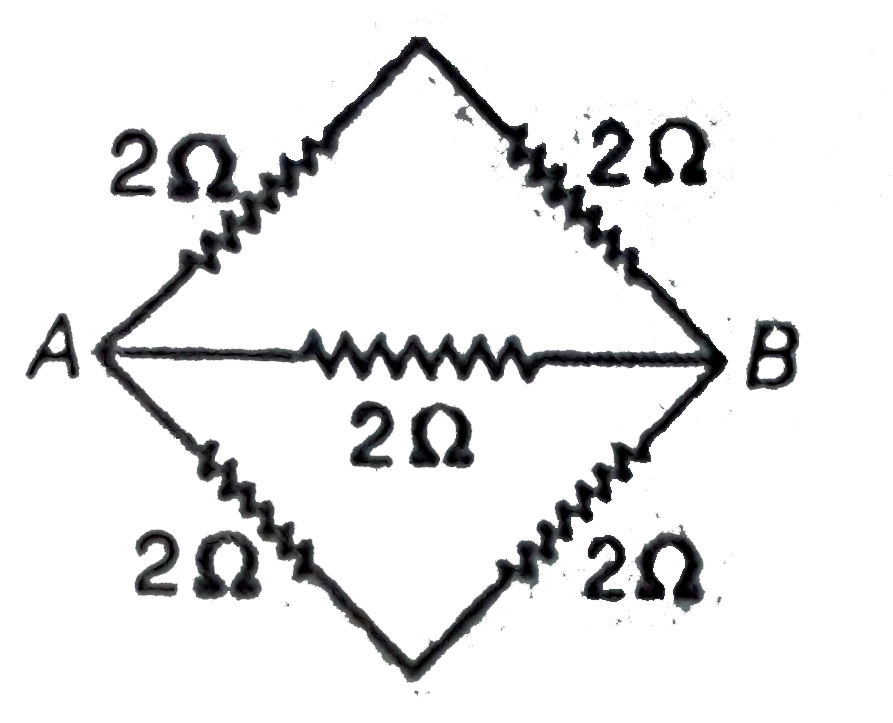 A2ΩB4ΩC8ΩD1Ω
A2ΩB4ΩC8ΩD1ΩIn the netwrok shown in fig. each resistance is R.

The equivalent resistance between A and B isA3R4B5R6C7R12D4R3
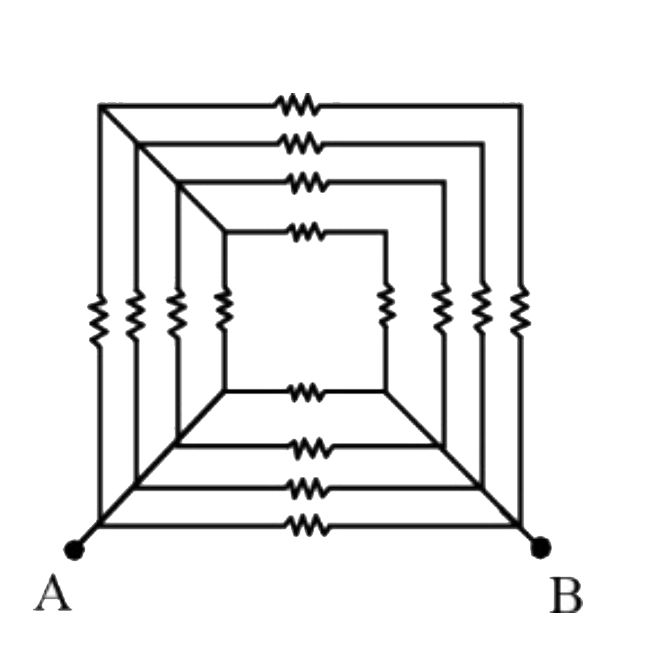
In the adjacent circuit diagram , each resister is of 16Ω . The equivalent resistance between A and B is
View SolutionIn the netwrok shown in fig. each resistance is R.

The equivalent resistance between A and G is
View SolutionIn the netwrok shown in fig. each resistance is R.

The equivalent resistance between A and C is
View SolutionThe equivalent resistance between A and B will be (in Ω)
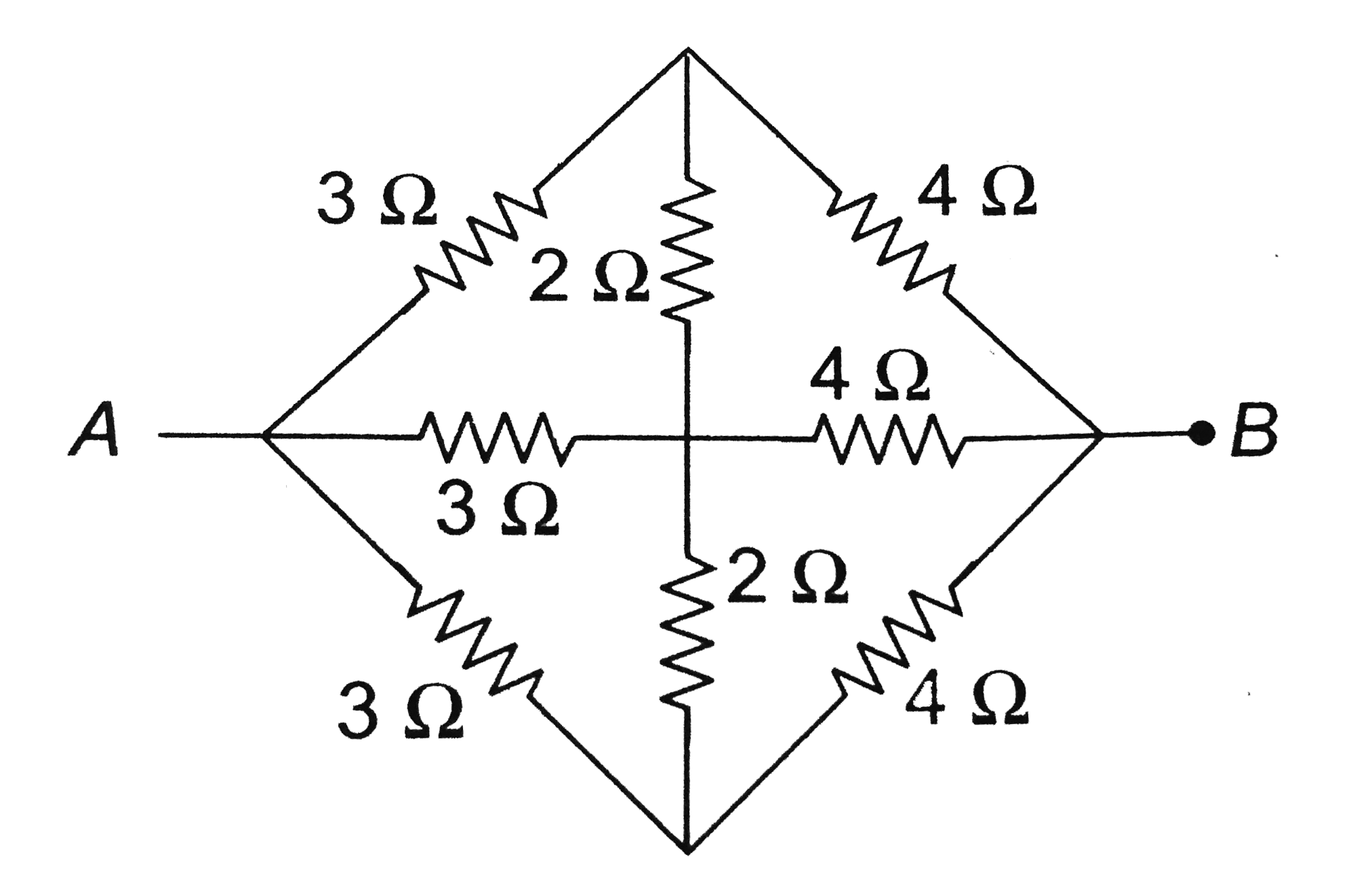
View SolutionIn the circuit shown, the value of each resistance is r , then equivalent resistance of circuit between points A and B will be

View Solution