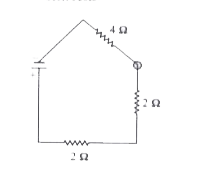
The equivalent resistance of the following infinite network of resistance is
A
Less than 4Ω
B
4Ω
C
More than 4Ω but less than 12Ω
D
12Ω
Video Solution
Text Solution
The correct Answer is:C
(c ) R=2+2+2×R2+R⇒2R+R2=8+4R+2R
⇒R2−4R−8=0⇒R=4±√16+322=2±2√3
R cannot be negative, hence R=2+2√3=5.46Ω
|
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:A2ZChapter:CURRENT ELECTRICITYExercise:Kircoff'S Laws And Simple Circuits
Explore 64 Videos
- CURRENT ELECTRICITYBook:A2ZChapter:CURRENT ELECTRICITYExercise:R-C Circuits
Explore 17 Videos
- CURRENT ELECTRICITYBook:A2ZChapter:CURRENT ELECTRICITYExercise:Section D - Chapter End Test
Explore 29 Videos
- ATOMIC PHYSICSBook:A2ZChapter:ATOMIC PHYSICSExercise:Section D - Chapter End Test
Explore 30 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:A2ZChapter:DUAL NATURE OF RADIATION AND MATTERExercise:Section D - Chapter End Test
Explore 30 Videos
Similar Questions
Knowledge Check
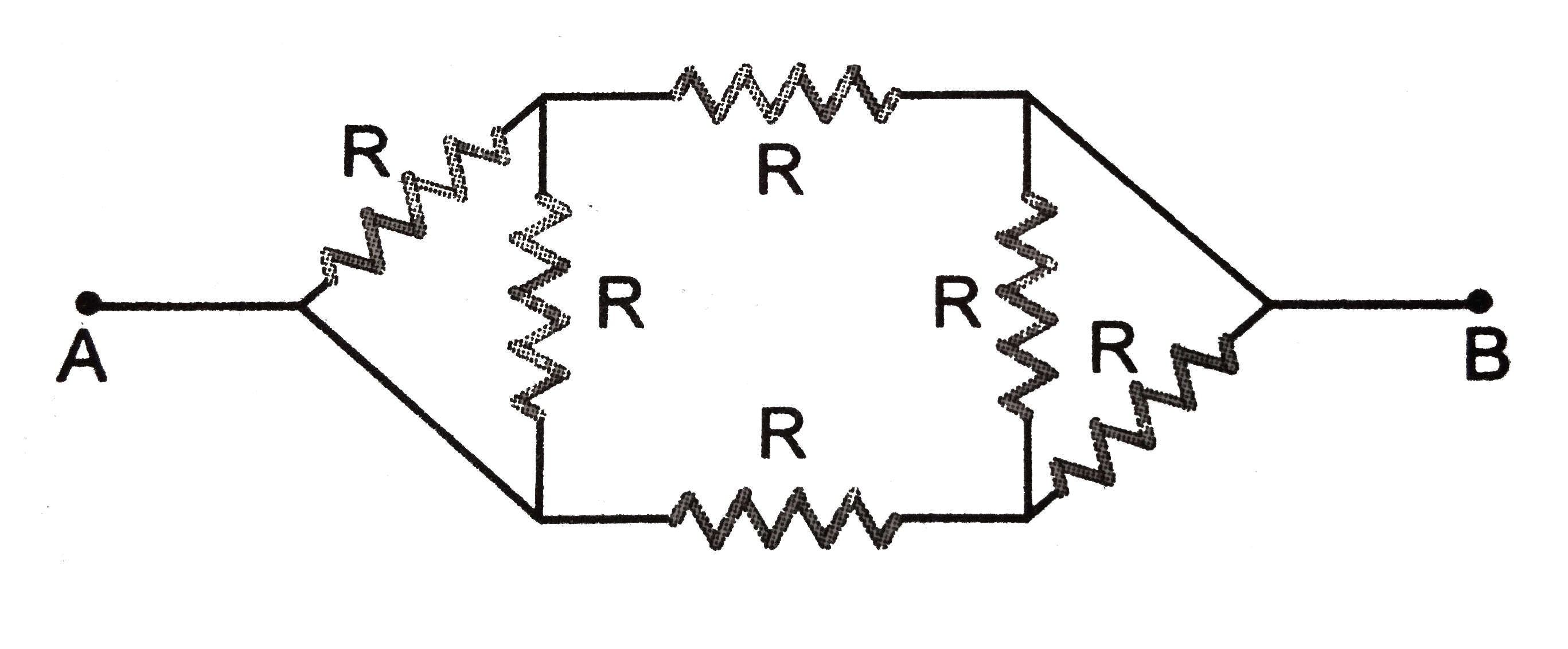
The equivalent resistance of the following diagram A and B is
 A23ΩB9ΩC6ΩDNone of these
A23ΩB9ΩC6ΩDNone of theseThe equivalent resistance between point A and B of an infinite network of resistance, each of 1Ω, connected as shown, is
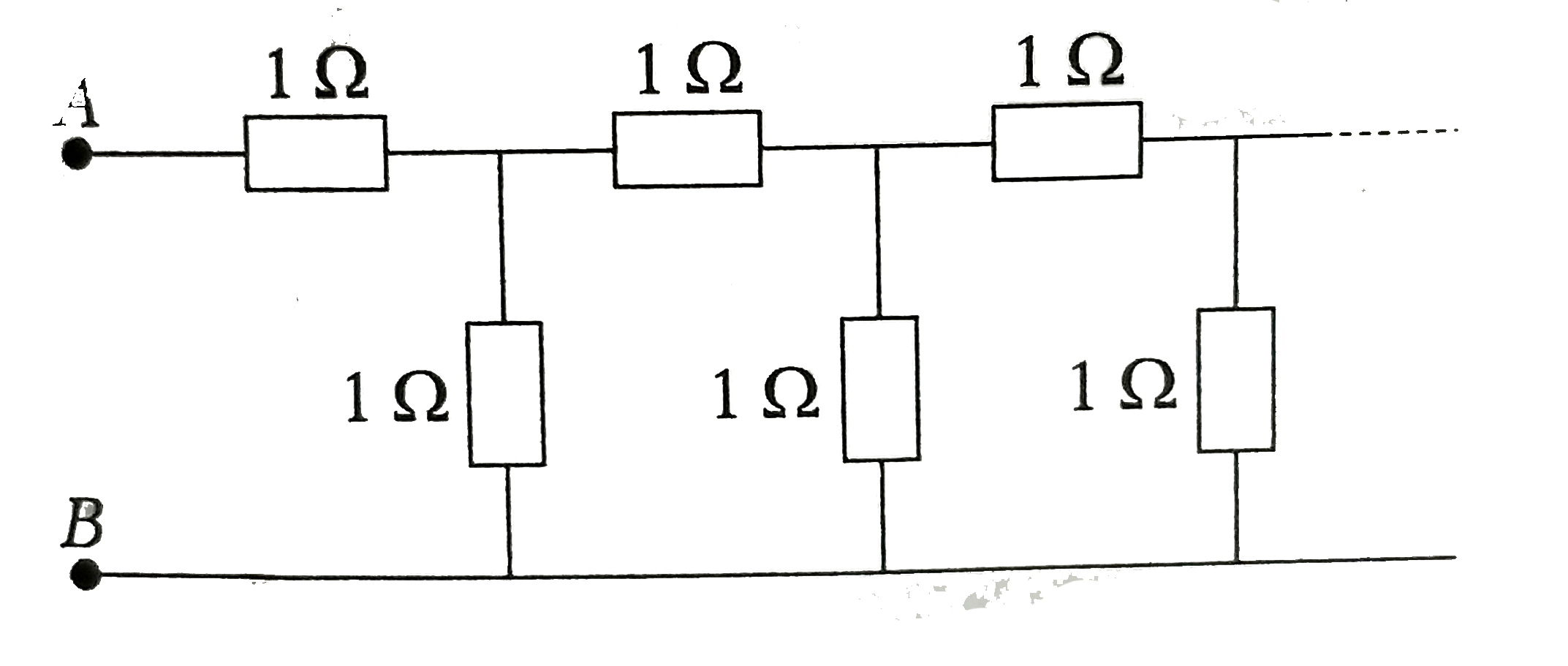 AinfiniteB2ΩC1+√52ΩDzero
AinfiniteB2ΩC1+√52ΩDzeroThe equivalent resistance across AB in the given network is
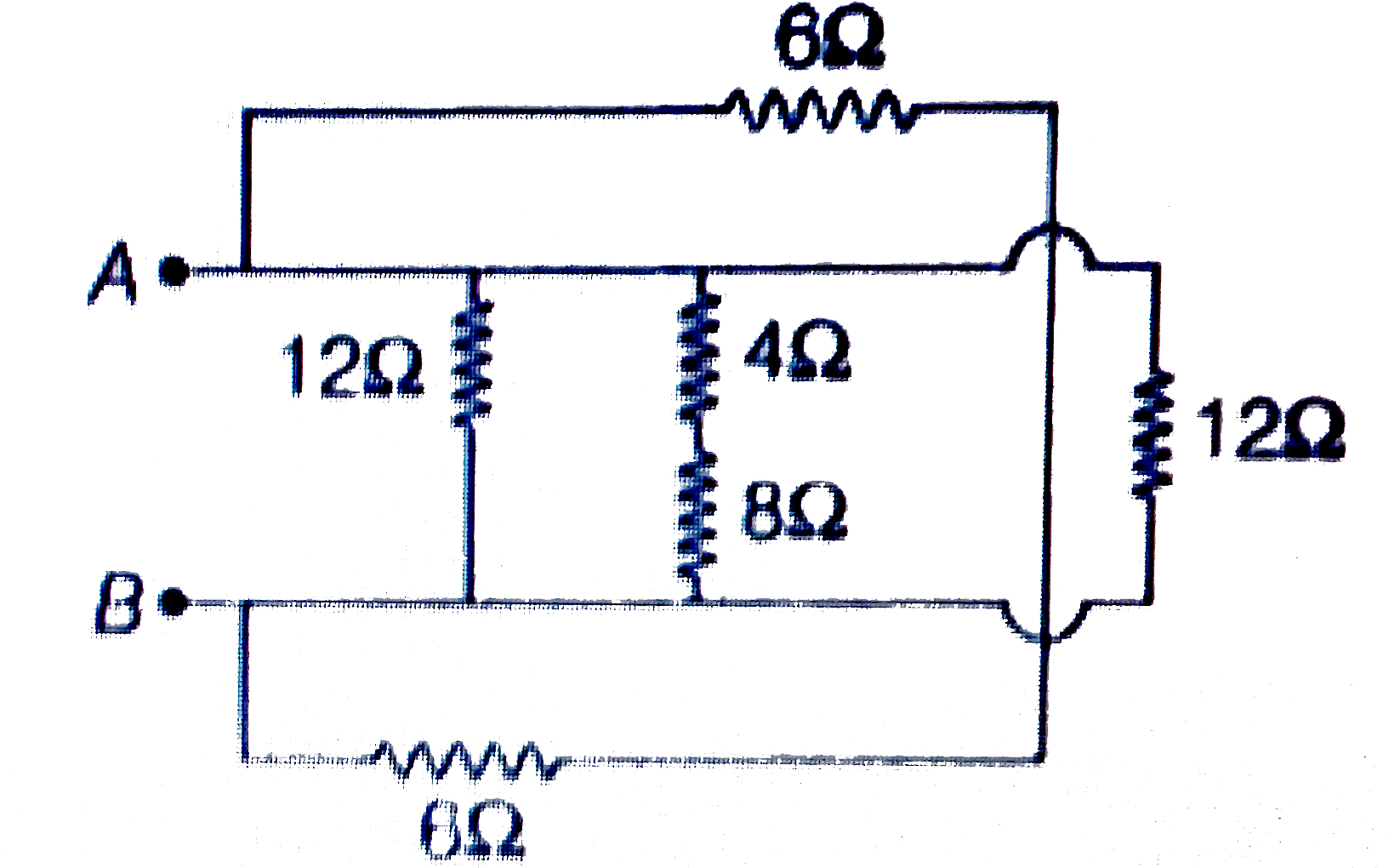 A4ΩB3ΩC12ΩD43Ω
A4ΩB3ΩC12ΩD43Ω
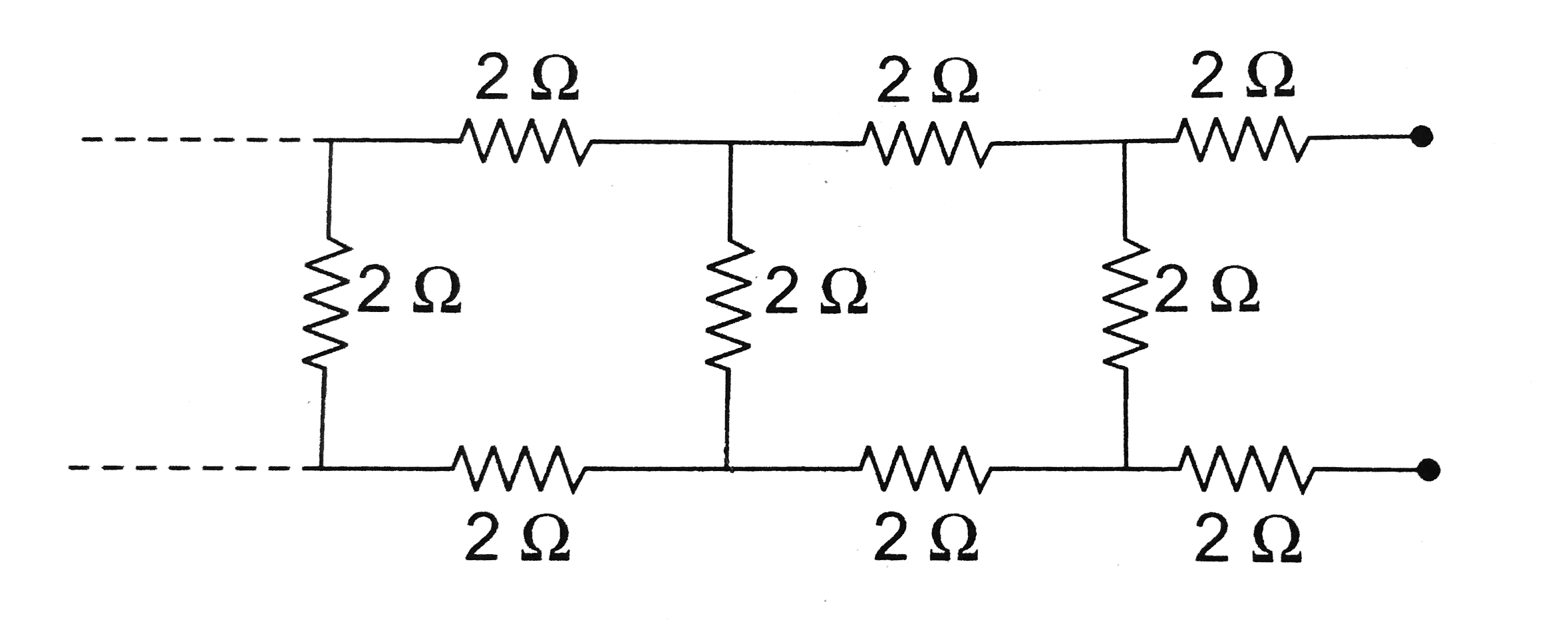
What is the equivalent resistance between points A and B of the networks of resistors.
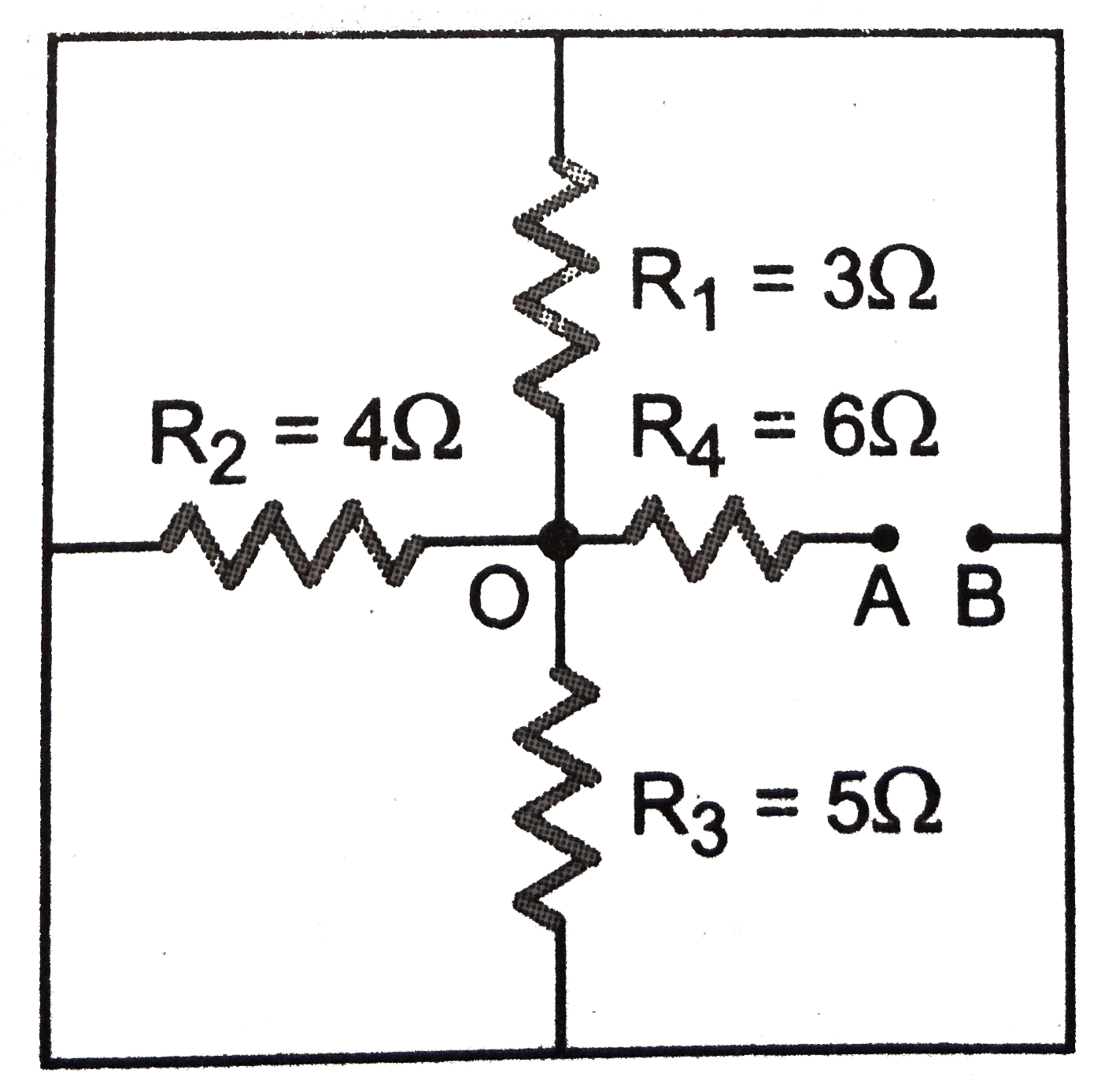
View Solution
The equivalent resistance between points A and B of an infinite network of resistance each of 1Ω connected as shown is
View SolutionThe equivalent resistance between points A and B of an infinite network of resistances each of 1Ω connected as shown, is
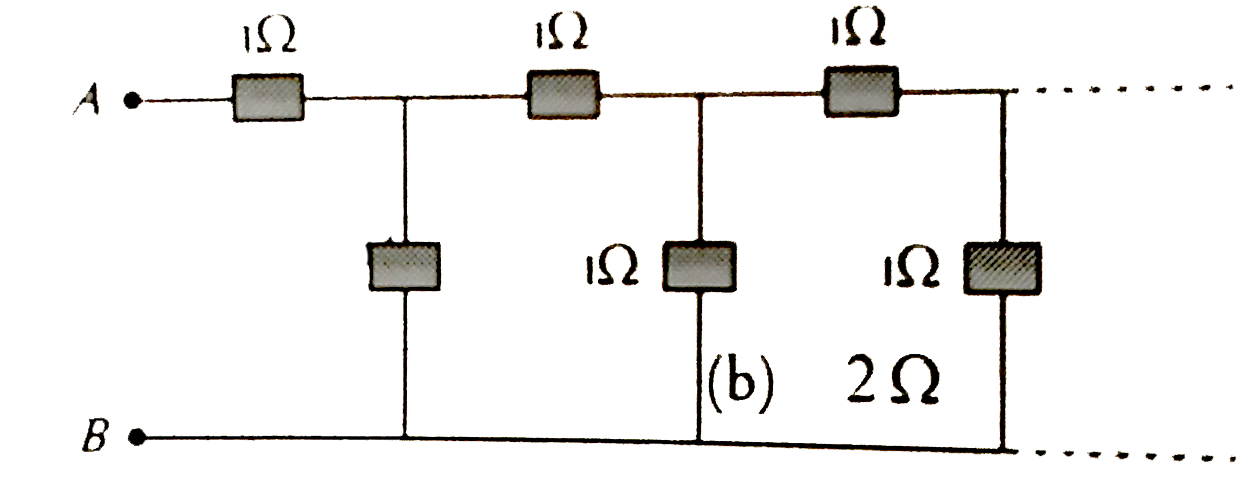
View SolutionEquivalent resistance (in ohm) of the given network is
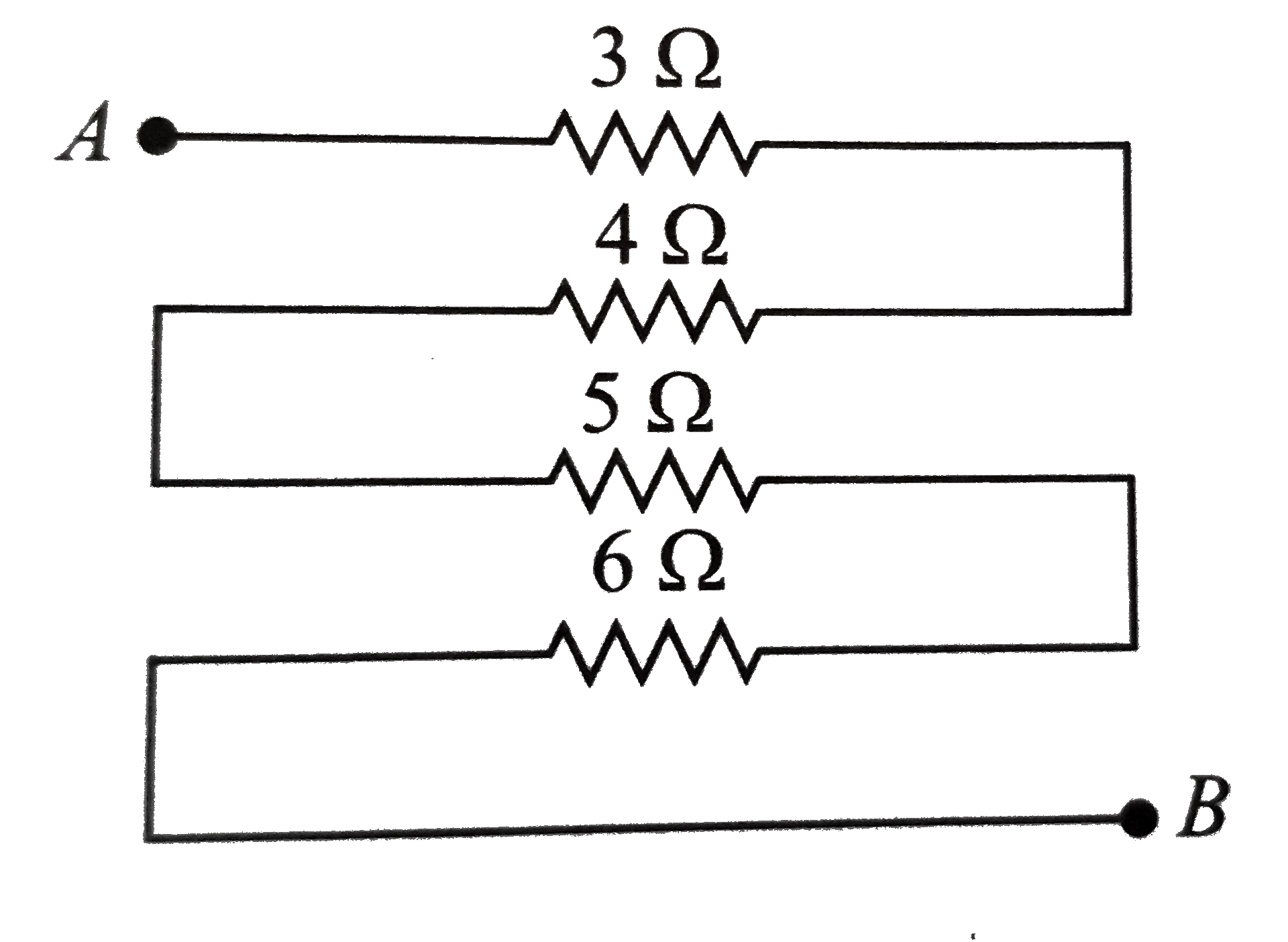
View SolutionThe equivalent resistance between point A and B of an infinite net work of resistances each of 1Ω connected
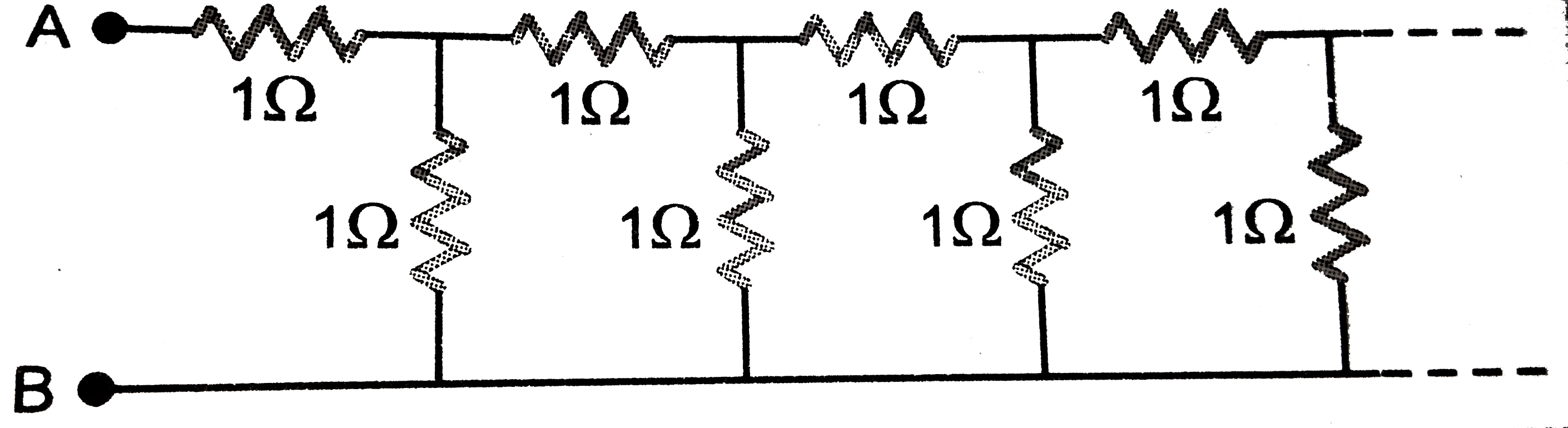
View Solution