One mole of a gas in the state A(P1,V1,T1) is subjected to adiabatic expansion to attain state B(P2,V2,T2). The work done by the gas is:
−R(T1−T2)γ−1
nR(T2−T1)γ−1
R(T2−T1)1−γ
P2V2−P1V11−γ
The correct Answer is:A
To calculate the work done by one mole of a gas during an adiabatic expansion from state A to state B, we can follow these steps:
1. Understand the Adiabatic Process:
- In an adiabatic process, there is no heat exchange with the surroundings. The work done by the gas results in a change in its internal energy.
2. Identify Given Parameters:
- We have one mole of gas (n = 1).
- The initial state A has parameters: P1,V1,T1.
- The final state B has parameters: P2,V2,T2.
3. Use the Formula for Work Done in Adiabatic Process:
- The work done W by the gas during an adiabatic expansion can be calculated using the formula:
W=nR(T2−T1)γ−1
- Where:
- n = number of moles (1 mole in this case)
- R = universal gas constant
- T1 = initial temperature
- T2 = final temperature
- γ = heat capacity ratio (C_p/C_v)
4. Substituting the Values:
- Since n=1, the equation simplifies to:
W=R(T2−T1)γ−1
5. Conclusion:
- The work done by the gas during the adiabatic expansion from state A to state B is:
W=R(T2−T1)γ−1
Final Answer:
The work done by the gas in the adiabatic expansion is R(T2−T1)γ−1.
---
- In an adiabatic process, there is no heat exchange with the surroundings. The work done by the gas results in a change in its internal energy.
- We have one mole of gas (n = 1).
- The initial state A has parameters: P1,V1,T1.
- The final state B has parameters: P2,V2,T2.
- The work done W by the gas during an adiabatic expansion can be calculated using the formula:
W=nR(T2−T1)γ−1
- Where:
- n = number of moles (1 mole in this case)
- R = universal gas constant
- T1 = initial temperature
- T2 = final temperature
- γ = heat capacity ratio (C_p/C_v)
- Since n=1, the equation simplifies to:
W=R(T2−T1)γ−1
- The work done by the gas during the adiabatic expansion from state A to state B is:
W=R(T2−T1)γ−1
The work done by the gas in the adiabatic expansion is R(T2−T1)γ−1.
Topper's Solved these Questions
Similar Questions
A gas with cpcV=γ goes from an intial state (p1,V1,T1) to a final state (p2,V2,T2) through an adiabatic process. The work done by the gas is
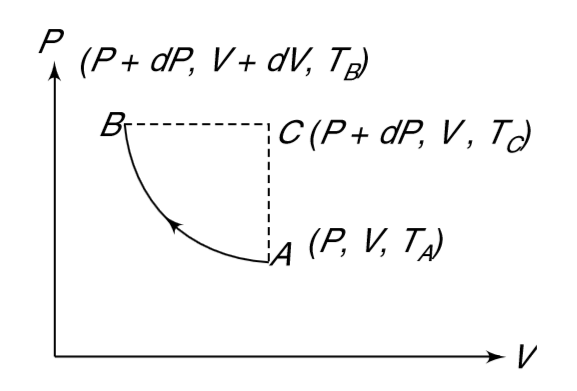
View SolutionOne mole of a gas is in state A[P,V,TA]. A small adiabatic process causes the state of the gas to change to B[P+dP,V+dV,TB]. The changes dV & dP are infinitesimally small and dV is negative. An alternative process takes the gas from state A to B via A→C→B. A→C is isochoric and C→B is isobaric path. State at C is [P+dP,V,TC].
(a) Rank the temperatures TA,TB and TC from highest to lowest.
(b) Find g of the gas in terms of TA, TB and TC.
View Solution
Knowledge Check
If a system undergoes an adiabatic change from state 1 to state 2, the work done by the gas is:
AU1−U2BU2−U1CCV(T2−T2)D12(P1V2−P1V1)An ideal gas is transformed from state A(P1,V1) to the state B(P2,V2) through path AB. In this process the work done by the gas is
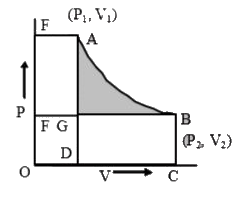 AW = area ABCDABW = area ABEFACW = area ABGADW = area ABCOFA
AW = area ABCDABW = area ABEFACW = area ABGADW = area ABCOFAA gas expands under constant pressure P from volume V1 toV2The work done by the gas is
AP(V2−V1)BP(V1−V2)CP(Vλ1−Vλ2)DPV1V2V2−V1
An ideal gas, in initial state 1(P1,V1,T1) is cooled to a state 3(P3,V3,T3) by a process which can be represented by a straight one on the P–V graph. The same gas in a different initial state 2 (P2,V2,T1) is cooled to same final state 3 (P3,V3,T3) by a process which can also be represented by a straight line on the same P–V graph. Q1 and Q2 are heat rejected by the gas in the two processes. Which is larger Q1 or Q2. It is given that P_(1) gt P_(2).
View SolutionIf a gas of a volume V1 at pressure p1 is compressed adiabatically to volume V2 and pressure p2, calculate the work done by the gas.
View SolutionOne mole of hydrogen, assumed to be ideal, is adiabatically expanded from its initial state (P1,V1,T1) to the final state (P2,V2,T2). The decrease in the internal energy of the gas during this process will be given by
View SolutionOne mole of an ideal gas at temperature T expands slowly according to the law pV= constant.
Its final temperature is T2. The work done by the gas is
View SolutionOne mole of an ideal gas at temperature T1 expends according to the law PV2=a (constant). The work done by the gas till tempereature of gas becomes T2 is
View Solution