One mole of a gas is in state A[P,V,TA]. A small adiabatic process causes the state of the gas to change to B[P+dP,V+dV,TB]. The changes dV & dP are infinitesimally small and dV is negative. An alternative process takes the gas from state A to B via A→C→B. A→C is isochoric and C→B is isobaric path. State at C is [P+dP,V,TC].
(a) Rank the temperatures TA,TB and TC from highest to lowest.
(b) Find g of the gas in terms of TA, TB and TC.
![One mole of a gas is in state A[P, V, T(A)]. A small adiabatic process causes the state of the gas to change to B [P + dP, V + dV, T(B)]. The changes dV & dP are infinitesimally small and dV is negative. An alternative process takes the gas from state A to B via A rarr C rarr B. A rarr C is isochoric and C rarr B is isobaric path. State at C is [P + dP, V, T(C)]. (a) Rank the temperatures T(A), T(B) and T(C) from highest to lowest. (b) Find g of the gas in terms of T(A), T(B) and T(C).](https://d10lpgp6xz60nq.cloudfront.net/physics_images/IJA_PHY_V02_C04_E01_032_Q01.png)
The correct Answer is:(a) TC>TB>TA , (b) γ=TC−TATC−TB
Step by step video, text & image solution for One mole of a gas is in state A[P, V, T_(A)]. A small adiabatic process causes the state of the gas to change to B [P + dP, V + dV, T_(B)]. The changes dV & dP are infinitesimally small and dV is negative. An alternative process takes the gas from state A to B via A rarr C rarr B. A rarr C is isochoric and C rarr B is isobaric path. State at C is [P + dP, V, T_(C)]. (a) Rank the temperatures T_(A), T_(B) and T_(C) from highest to lowest. (b) Find g of the gas in terms of T_(A), T_(B) and T_(C). by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - ARIHANTCHAPTER - FIRST LAW OF THERMODYNAMICSEXERCISE - Level 36videos
FIRST LAW OF THERMODYNAMICS
- BOOK - ARIHANTCHAPTER - FIRST LAW OF THERMODYNAMICSEXERCISE - Level 36videos
FIRST LAW OF THERMODYNAMICS
- BOOK - ARIHANTCHAPTER - ELASTICITYEXERCISE - Level 31videos
ELASTICITY
- BOOK - ARIHANTCHAPTER - FLUIDSEXERCISE - All Questions70videos
FLUIDS
Similar Questions
An adiabatic cylinder of cross section A is fitted with a mass less conducting piston of thickness d and thermal conductivity K. Initially, a monatomic gas at temperature T0 and pressure P0 occupies a volume V0 in the cylinder. The atmospheric pressure is P0 and the atmospheric temperature is T1(>T0). Find
(a) the temperature of the gas as a function of time
(b) the height raised by the piston as a function of time.
Neglect friction and heat capacities of the container and the piston.05:27View SolutionAn adiabatic cylinder of cross section A is fitted with a mass less conducting piston of thickness d and thermal conductivity K. Initially, a monatomic gas at temperature T0 and pressure P0 occupies a volume V0 in the cylinder. The atmospheric pressure is P0 and the atmospheric temperature is T1(>T0). Find
(a) the temperature of the gas as a function of time
(b) the height raised by the piston as a function of time.
Neglect friction and heat capacities of the container and the piston.04:10View SolutionA metal cylinder of length L and radius R is fixed rigidly to ground with its axis vertical. A twisting torque τ0 is applied along the circumference at the top of the cylinder. This causes an angular twist of θ0 (rad) in the top surface. Calculate the shear modulus of elasticity (η) of the material of the cylinder.
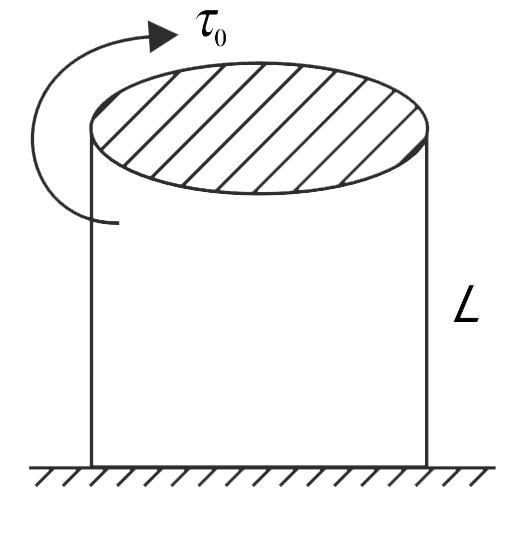03:38View SolutionWe know that the atmospheric pressure on the surface of the earth is because of weight, of the air. The radius of the earth is 6400 km and atmospheric pressure on the sruface of earth is 1×105N/m2. Estimate the mass of the earth's atmosphere assuming that acceleration due to gravity remains constant at 10m/s2 over the entrie height of the atmospehre.
03:46View SolutionAn ideal gas (2.0 moles) is carried round a cycle as shown. If the process b→c is isothermal and CV=3cal/mol/K. Determine
a. work done,
b. change in internal energy,
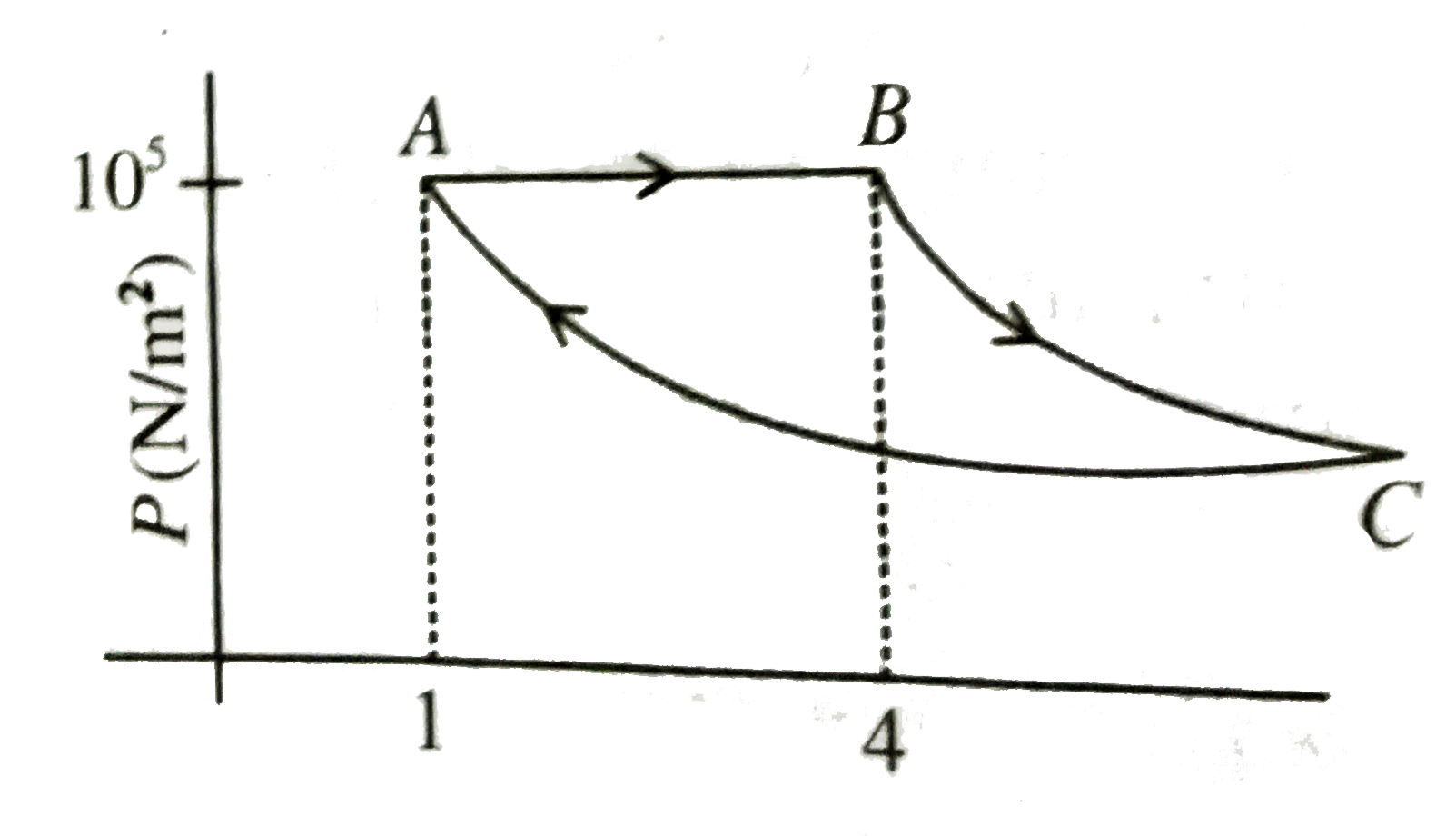
c. heat supplied to the system during processes a→b, b→c and c→a.03:46View SolutionP-V curve of a diatomic gas is shown in the Fig. Find the total heat given to the gas in the process A→B→C
05:07View SolutionOne mole of a monatomic gas is taken from a point A to another point B along the path ACB . The initial temperature at A is T_(0) . Calculate the heat abosrbed by the gas in the process A rarr C rarr B .
01:17View SolutionA fixed mass of gas is taken through a process A→B→C→A. Here A→B is isobaric, B→C is adiabatic and C→Ais isothermal.
Find pressure at C.02:43View SolutionA fixed mass of gas is taken through a process A rarr B rarr C rarrA . Here A rarr B is isobaric, B rarr C is adiabatic and C rarr A is isothermal. Find volume at C .
02:55View SolutionAn ideal gas undergoes a series of processes represented bya→B→C→D on the P-V diagram. Answer the following questions.
(a) Is the internal energy of the gas at B and D equal?
(b) Find work done by the gas in the process A rarr B rarr C rarr D.
(c) Is it right to say that point B and D lie on an isotherm?
(d) Find the ratio of internal energy of the gas in state A to that in state D.
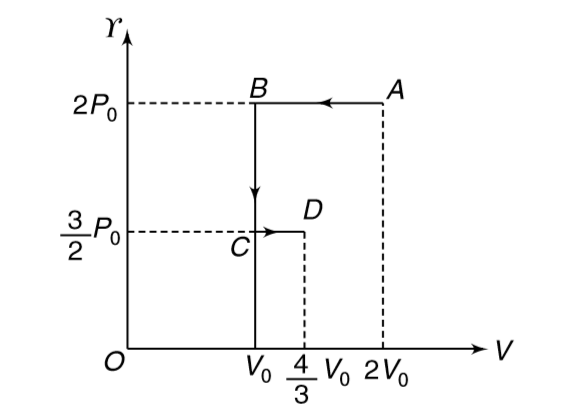10:49View SolutionFive moles of gas is put through a series of changes as shown graphically in a cyclic process the A→B,B→C and C→A respectively are
02:02View SolutionFor an adiabatic change the value of dPP is equal to (dV= change in vol.,γ=CpCv):
03:31View SolutionIn a cyclic process shown in the figure on ideal gas is adiabatically taken from B to A, the work done on the gas during the process B rarr A is 30J, when the gas is taken from A rarr B the heat absorbed by the gas is 20J. What is the change in internal ebergy of the gas in the process A rarr B .
03:09View SolutionAn ideal gas (2.0 moles) is carried round a cycle as shown. If the process b→c is isothermal and CV=3cal/mol/K. Determine
a. work done,
b. change in internal energy,
c. heat supplied to the system during processes a→b, b→c and c→a.02:31View SolutionP-V curve of a diatomic gas is shown in the Fig. Find the total heat given to the gas in the process A→B→C
01:34View Solution