One mole of hydrogen, assumed to be ideal, is adiabatically expanded from its initial state $(P_{1}, V_{1}, T_{1})$ to the final state $(P_{2}, V_{2}, T_{2})$ . The decrease in the internal energy of the gas during this process will be given by

$C_{V} (T_{1} - T_{2})$

$C_{P} (T_{1} - T_{2})$

$\frac{C_{P} + C_{V}}{2} (T_{1} - T_{2})$

$(C_{P} - C_{V}) (T_{1} - T_{2})$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Answer

Step by step video, text & image solution for One mole of hydrogen, assumed to be ideal, is adiabatically expanded from its initial state (P_(1), V_(1), T_(1)) to the final state (P_(2), V_(2), T_(2)). The decrease in the internal energy of the gas during this process will be given by by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS RACE

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
One mole of helium is adiabatically expanded from its initial state $(P_{i}, V_{i}, T_{i})$ to its final state $(P_{f}, V_{f}, T_{f})$ . The decrease in the internal energy associated with this expansion is equal to
A $C_{V} (T_{i} - T_{f})$
B $C_{P} (T_{i} T_{f})$
C $\frac{1}{2} (C_{P} + C_{V}) (T i - T f)$
D $(C_{p} + C_{V}) (T_{i} - T_{f})$
Question 2 - Select One or More
An ideal gas is expand from $(p_{1}, V_{1}, T_{1})$ to $(p_{2}, V_{2}, T_{2})$ under different conditions. The correct statement(s) among the following is (are):
AThe work done by the gas is less when it is expanded reversibly from $V_{1}$ to $V_{2}$ under adiabatic conditions as compared to that when expanded reversibly from $V_{1}$ to $V_{2}$ under isothermal conditions
BThe change in internal energy of the gas is (i) zero, if it is expanded reversibly with $T_{1} = T_{2}$ , and (ii) positive, if it is expanded reversibly under adiabatic conditions with $T_{1} \neq T_{2}$
CIf the expansion is carried out freely, it is simultaneously both isothermal as well as adiabatic
DThe work done on the gas is maximum when it is compressed irreversibly from $(P_{2}, V_{2})$ to $(P_{1}, V_{1})$ against constant pressure $P_{1}$
Question 3 - Select One
An ideal gas is transformed from state A $(P_{1}, V_{1})$ to the state B $(P_{2}, V_{2})$ through path AB. In this process the work done by the gas is

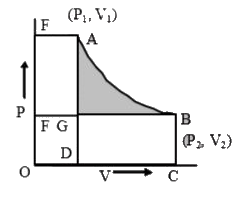AW = area ABCDA
BW = area ABEFA
CW = area ABGA
DW = area ABCOFA

ALLEN-RACE-Basic Maths (Thermal Physics) (Thermodynamic process)

Home
Ask Doubt
Profile

One mole of hydrogen, assumed to be ideal, is adiabatically expanded from its initial state (P1,V1,T1) to the final state (P2,V2,T2). The decrease in the internal energy of the gas during this process will be given by

The correct Answer is:A

Topper's Solved these Questions

Similar Questions

Knowledge Check

One mole of helium is adiabatically expanded from its initial state (Pi,Vi,Ti) to its final state (Pf,Vf,Tf). The decrease in the internal energy associated with this expansion is equal to

An ideal gas is expand from (p1,V1,T1) to (p2,V2,T2) under different conditions. The correct statement(s) among the following is (are):

An ideal gas is transformed from state A(P1,V1) to the state B(P2,V2) through path AB. In this process the work done by the gas is

ALLEN-RACE-Basic Maths (Thermal Physics) (Thermodynamic process)

One mole of hydrogen, assumed to be ideal, is adiabatically expanded from its initial state $(P_{1}, V_{1}, T_{1})$ to the final state $(P_{2}, V_{2}, T_{2})$ . The decrease in the internal energy of the gas during this process will be given by

One mole of helium is adiabatically expanded from its initial state $(P_{i}, V_{i}, T_{i})$ to its final state $(P_{f}, V_{f}, T_{f})$ . The decrease in the internal energy associated with this expansion is equal to

An ideal gas is expand from $(p_{1}, V_{1}, T_{1})$ to $(p_{2}, V_{2}, T_{2})$ under different conditions. The correct statement(s) among the following is (are):

An ideal gas is transformed from state A $(P_{1}, V_{1})$ to the state B $(P_{2}, V_{2})$ through path AB. In this process the work done by the gas is