Determine the period of oscillations of mercury of mass m=200g poured into a bent tube (figure) whose right arm forms an angle θ=30∘ with vertical. The cross-sectional area of the tube is S=0.50cm2. The viscosity of mercury is to be neglected.
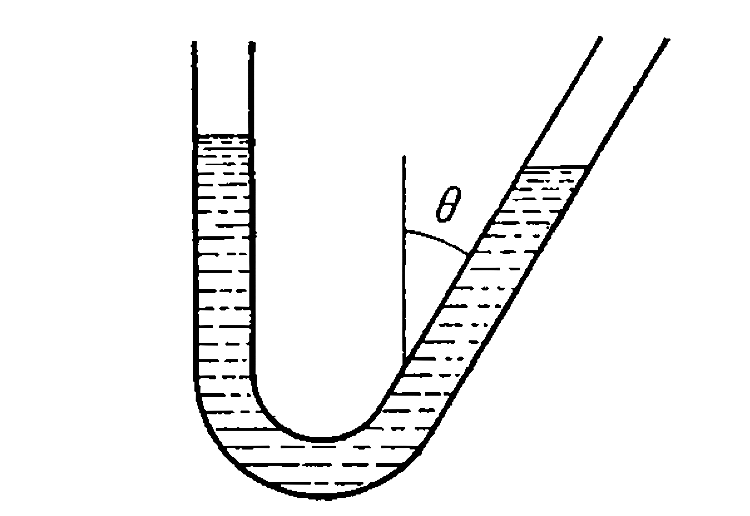
Let A be the uniform cross-sectional area of the tube. Let the level of liquid of density ρ be depressed in the vertical arm of tube by distance y . The verticall rise of liquid in the slant portion of the tube =ycosθ.
The vertical difference in liquid level in two arms of bent tuve −y+ycosθ=(1+cosθ)y in two arms of bent tube will provide a restoring force to the liquid. So restoring force on the liquid is
F=−[ weight of the liquid column of height (1+cosθ(y]
=−(1−cosθ)yρgA
=−(1+cosθ)Aρgy ...(i)
Since F∝y and F is directed towards equilibrium position of liquid in two arms of bent tube, hence if the force is removed or liquid is left free, it will execute SHM in bent tube.
Comparing (i), with , F=−ky
We have, spring factore, k=(1+cosθ)Aρg.
Here, inertia factore = mass of mercury =m=200g
Period of oscillation, T=2π√inertiafactorspringfactor
=2×2270√200(1+cos30∘)×0.5×13.6×980
=0.8s
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - NCERT EXERCISES WITH SOLUTIONS19videos
OSCILLATIONS AND WAVES
- BOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Additional Exercises6videos
OSCILLATIONS AND WAVES
- BOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Long Answer Questions33videos
OSCILLATIONS AND WAVES
- BOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks5videos
MATHEMATICAL TOOLS
- BOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance18videos
PHYSICAL WORLD AND MEASUREMENT
Similar Questions
The period of oscillations of mercury of mass m ,density ρ poured into a uniform bent tube,as shown in figure,whose right arm forms an angle θ=30∘ with the vertical and whose left arm is vertical is T seconds.The cross - sectional area of the tube is S. The viscosity of mercury is to be neglected. If T is 2π√mρgS(x) ,then value of x is ( assume g= acceleration due to gravity & all parameters in S.I.units)
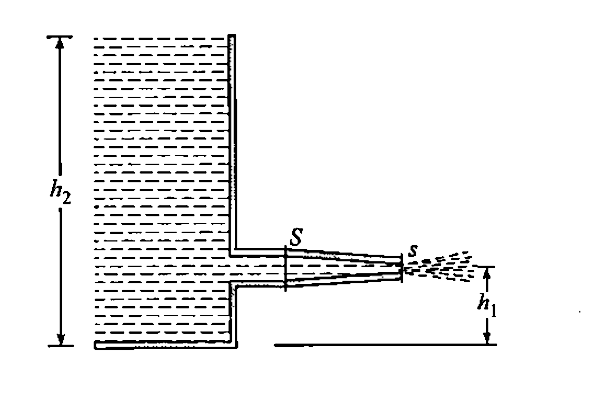
View SolutionA side wall of a wide open tank is provided with a narrowing tube (figure) through which water flows out. The cross-sectional area of the tube decreases from S=3.0cm2 to s=1.0cm2. The water level in the tank is h=4.6m higher than that in the tube. Neglecting the viscosity of the water, find the horizontal component of the force tending to pull the tube out of the tank.
 View Solution
View SolutionA side wall of a wide open tank is provided with a narrowing tube through which water flows out. The cross-sectional area of the tube decreases from S=3.0cm2 to s=1.0cm2. The water level in the tank is h=4.6m heigher than in the tube. Neglecting the viscosity of water, find the horizontal component of the force tending to pull the tube out of the tank.
 View Solution
View SolutionA U-shaped tube open to the air at both ends contains some mercury. A quantity of water is carefully poured into the left arm of the U-shaped tube until the vertical height of the water column is 15.0cm.
(a) What is the gauge pressure at the water mercury interface ?
(b) Calculate the vertical distance h from the top of the mercury in the right hand arm of the tube to the top of the water in the left-hand arm.
 .View Solution
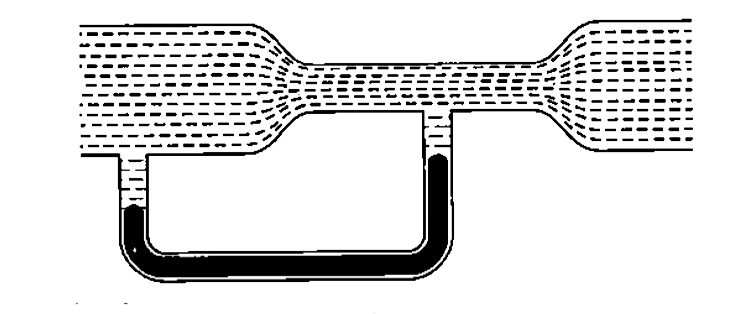
.View SolutionWater flows through the tubes shown in figure. The areas of cross-section of the wide and the narrow portions of the tube are 5cm2 and 2cm2 respectively. The rate of flow of water through the tube is 500cm3/s. Find the difference of mercury levels in the U-tube.
 View Solution
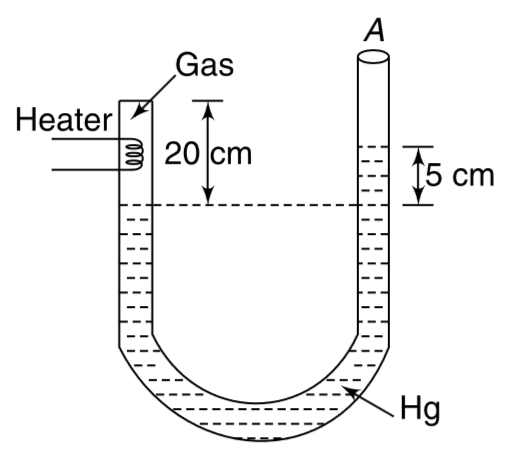
View SolutionOne end of an insulating U tube is sealed using insulating material. A mono atomic gas at temperature 300 K occupies 20 cm length of the tube as shown. The level of mercury on two sides of the tube differ by 5 cm. The other end of the tube is open to atmosphere. Area of cross section of the tube is uniform and is equal to 0.01m2. The gas in the tube is heated by an electric heater so as to raise its temperature to 562.5 K. Assume that no heat is conducted to mercury by the gas.
(a) Find the final length of the gas column.
(b) Find the amount of heat supplied by the heater to the gas.
 View Solution
View SolutionWater flows through the tube shown in figure. The areas of cross section of the wide and the narrow portions of the tube are 5cm2and2cm2 respectively. The rate of flow of water through the tube is 500cm3s−1 . Find the difference of mercury levels in the U-tube.
 View Solution
View SolutionA thin tube of uniform cross section is sealed at both ends. It lies horizontally, the middle 5cm containing mercury and the parts on its two sides containing air at the same pressure p. when the tube is held at and angle of 60∘ with the vertical, the length of the air column above and belw the mercury pellet are 46cm and 44.5cm respectively. Calculate the ressure - in centimeters of mercury, The timperature of the system is kept at 30∘C.
View SolutionA thin tube of uniform cross section is sealed at both ends. It lies horizontally, the middle 5cm containing mercury and the parts on its two sides containing air at the same pressure p. When the tube is held at and angle of 60∘ with the vertical, the length of the air column above and below the mercury pellet are 46cm and 44.5cm respectively. Calculate the pressure in centimeters of mercury, The temperature of the system is kept at 30∘C.
View SolutionA thread of mercury of 10.2 g is in a tube of uniform cross-section 0.1cm2. Calculate the length of the thread. The density of mercury is 13.6gcm3.
View Solution

