Question

Two identical glass rods $S_1$ and $S_2$ (refractive index=1.5) have one convex end of radius of curvature 10 cm. They are placed with the curved surfaces at a distance d as shown in the figure, with their axes (shown by the dashed line) aligned. When a point source of light P is placed inside rod $S_1$ on its axis at a distance of 50 cm from the curved face, the light rays emenating from it are found to be parallel to the axis inside $S_2$. The distance d is

Options

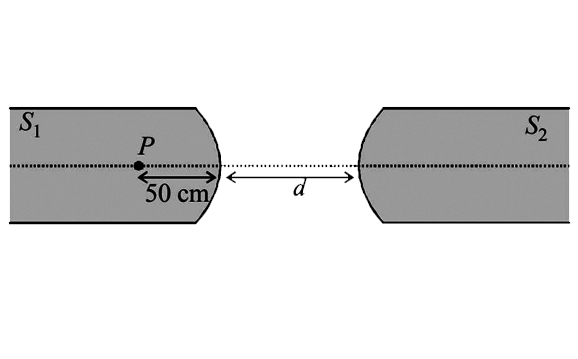
A. 60 cm
B. 70 cm
C. 80 cm
D. 90 cm

Answer

B

Explanation

For `S_1` (Refraction from denser to rarer medium)
`u = -50 cm, R = -10 cm`
`(mu_2)/(-u)+(mu_1)/(v)=(mu_1 - mu_2)/( R)`
`(3//2)/(-(-50))+(1)/(v)=(1 -3//2)/(-10)` or `(1)/(v)+(3)/(100)=(1)/(20)`
`(1)/(v)=(1)/(20)-(3)/(100)=(1)/(50)`
`v = 50 cm`
for `S_2` Refraction from rarer to denser medium
`:. u rarr -(d = 50), v = oo, R_2 = R`
`(mu_1)/(-u)+(mu_2)/(v)=(mu_2 - mu_1)/( R)`
`(1)/((d - 50))+ (3//2)/(oo) = (1)/(20)`
`d = 70 cm`.