Two identical coils each of radius 10cm and having number of turns 100 are lying in perpendicular planes, such that they have common centre. Find the resultant magnetic field at the centre of the coils if they carry currents 3A and 3√3A respectively.
The correct Answer is:3⋅77×10−3T
r1=r2=10cm=0⋅10m, n=100
I1=3A, I2=3√3A
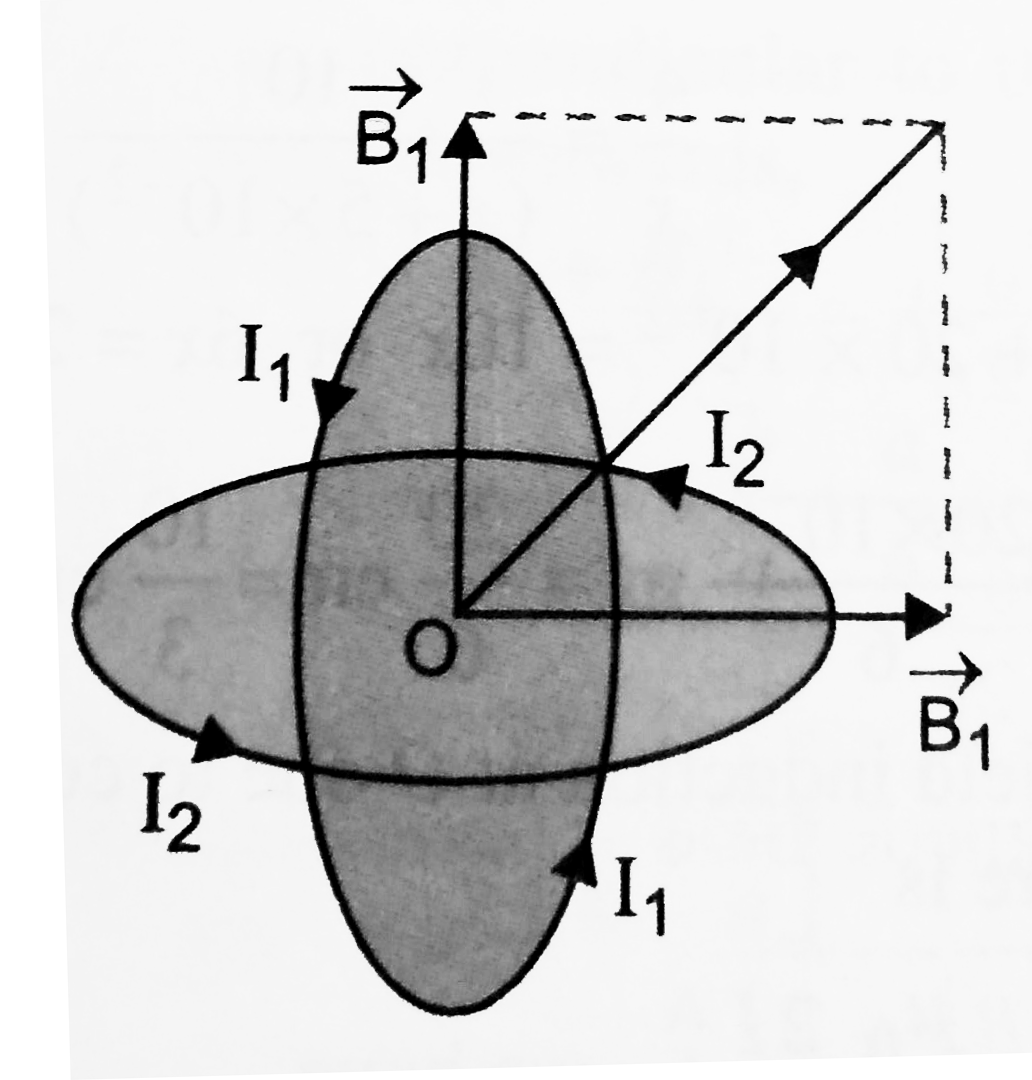
Magnetic field at centre O due to current I1 of the coil is
B1=μ04π2πnI1r1=μ0nI12r1
Magnetic field at centre O due to current I2 of the other coil is
B2=μ04π2πnI2r2=μ0nI22r2
Here, →B1 and →B2 are perpendicular to each other.
The resultant magnetic field at O is
B=√B21+B22=⎡⎣(μ0nI12r1)2+(μ0nI222r2)2⎤⎦1/2
=μ0n2[I21r21+I22r22]1/2
=(4π×10−7)×1002⎡⎢
⎢
⎢⎣32(0⋅1)2+(3√3)2(0⋅1)2⎤⎥
⎥
⎥⎦1/2
=2π×10−5×60=3⋅77+10−3T
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Test Your Grip (a)1videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Test Your Grip (c)1videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Value Based Questions2videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
- BOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - ASSERTION-REASON TYPE QUESTIONS2videos
ELECTROSTATICS
- BOOK - PRADEEPCHAPTER - OPTICSEXERCISE - Multiple choice questions1videos
OPTICS
Similar Questions
Two identical coils P and Q each of radius R are lying in perpendicular planes such that they have a common centre. Find the magnitude and PC direction of the magnetic field at the common centre of the two coils, if they carry currents equal to land √3I respectively.
 View Solution
View SolutionTwo identical loops P and Q each of radius 5cm are lying in perpendicular planes such that they have a common centre as shown in the figure. Find the magnitude and direction of the net field at the common centre of the two coils, if they carry currents equal to 3A and 4A respectively.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A circular coil of radius 10 cm having 100 turns carries a current of 3.2 A. The magnetic field at the center of the coil is
A2.01×10−3TB5.64×10−3TC2.64×10−3TD5.64×10−3T - Question 2 - Select One
Two identical coils carry equal currents have a common centre and their planes are at right angles to each other. The ratio of the magnitude of the resulatant magnetic field at the centre and the field due to one coil is
A2:1B1:2C√2:14D1:√2 - Question 3 - Select One
Two similar coils each of radius r and no. of turns n are lying concentrically with their planes at right angle to each other. The corrents folowing in them are 1 A and √3A respectively. What is the magnetic field at centre of the coils ?
Aμ0n2πrBμ0n√3πrCμonrD√3μ0nr
Two identical circular wires P and Q each of radius R and carrying current 'I' are kept in perpendicular planes such that they have a common centre as shown in fig. Find the magnitude and direction of the net magnetic field at the common centre of the two coils.
 View Solution
View SolutionTwo identical circular wires P and Q each of radius R and carrying current 'I' are kept in perpendicular planes such that they have a common centre as shown in the figure. Find the magnitude and direction of the net magnetic field at the common centre of the two coils.
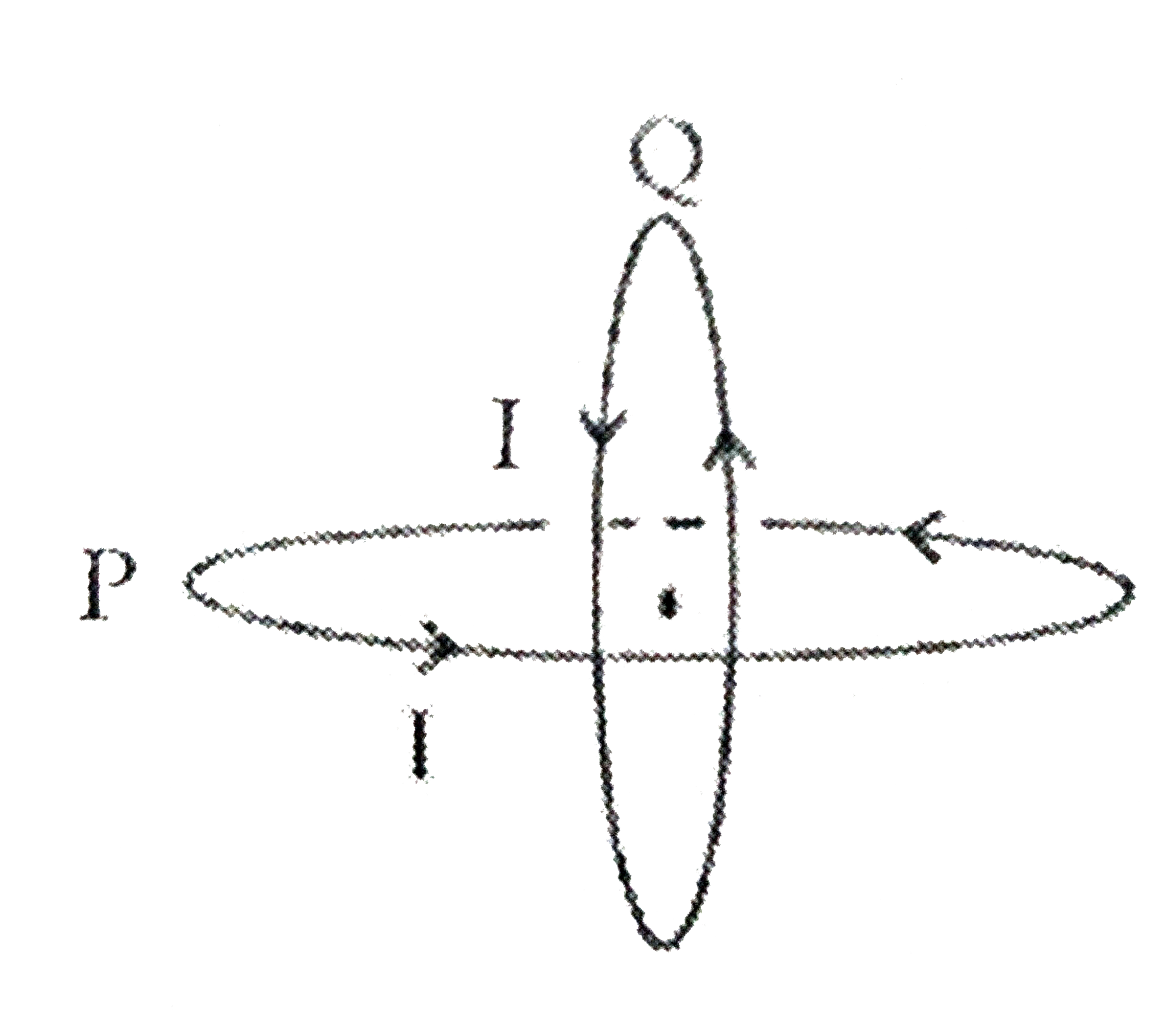 View Solution
View SolutionConsider a tightly wound 100 turn coil of radius 10 cm, carrying a current of 1 A. What is the magnitude of magnetic field at the centre of the coil?
View SolutionMagnetic field at the centre of a coil of 100 turns and radius 2×10−3 carrying 1 A current is:
View SolutionTwo similar coils of radius R and number of turns N are lying concentrically with their planes at an angle 60∘ to each other. The currents flowing in them are I and 2I respectively. The resultant magnetic induction at the centre will be
View Solution

