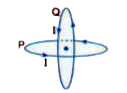
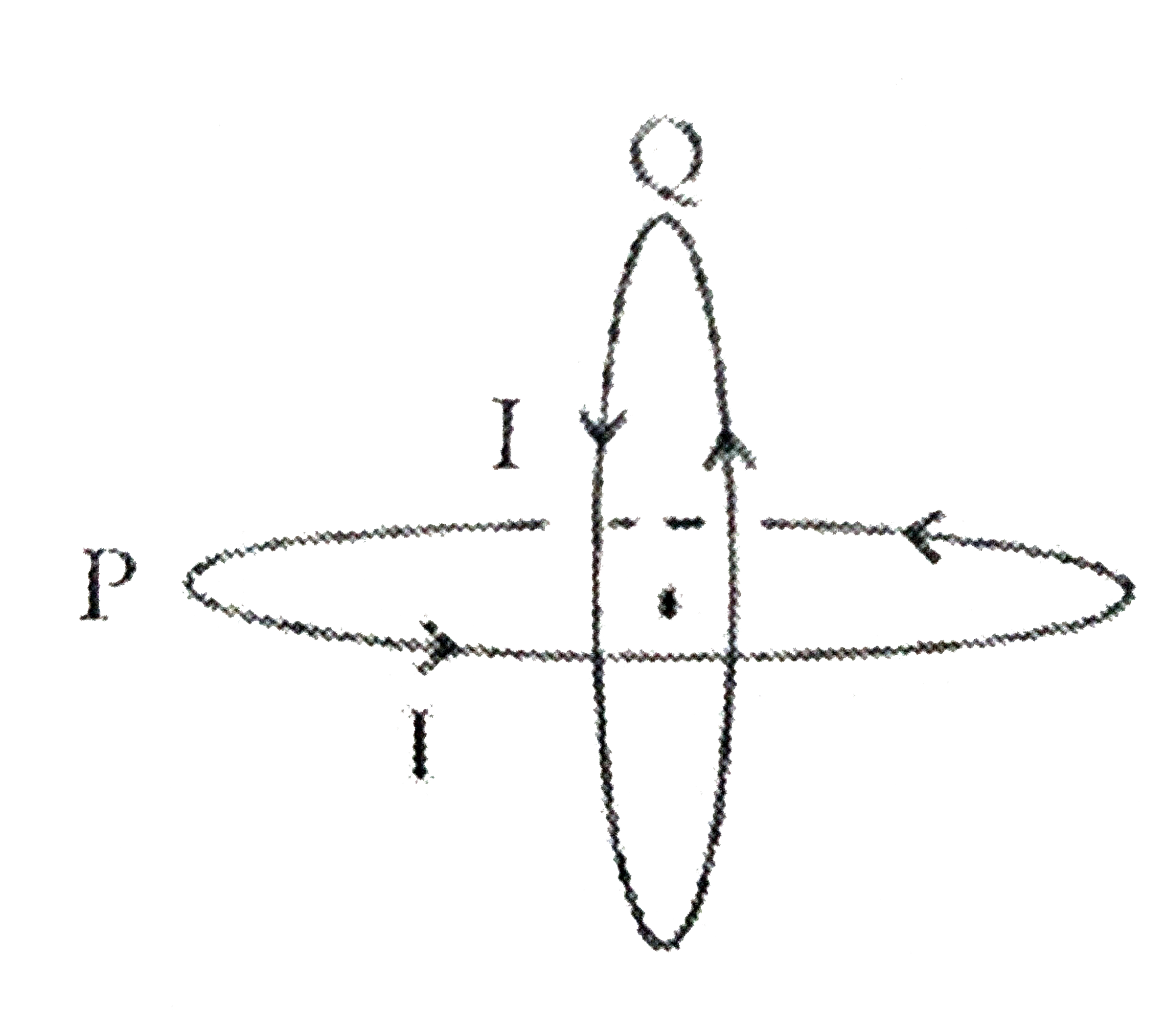
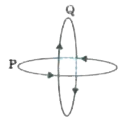
Two identical circular coils, P and Q, carrying currents 1A and √3A respectively, are placed concentrically and perpendicular to each other lying in the XY and YZ plane. Find the magnitude and direction of the net magnetic field at the centre of the coils.
The correct Answer is:μ0RT in X-Z plane
To solve the problem of finding the magnitude and direction of the net magnetic field at the center of two identical circular coils P and Q carrying currents 1A and √3A respectively, which are placed concentrically and perpendicular to each other, we can follow these steps:
Step 1: Calculate the Magnetic Field due to Coil P
The magnetic field B1 at the center of a circular coil is given by the formula:
B1=μ0I12R
where:
- I1=1A (current in coil P)
- μ0=4π×10−7T⋅m/A (permeability of free space)
- R is the radius of the coil (not given, but will cancel out later).
Substituting the values:
B1=4π×10−7×12R=2π×10−7RT
Step 2: Calculate the Magnetic Field due to Coil Q
Similarly, for coil Q, the magnetic field B2 is given by:
B2=μ0I22R
where:
- I2=√3A (current in coil Q).
Substituting the values:
B2=4π×10−7×√32R=2π√3×10−7RT
Step 3: Determine the Direction of the Magnetic Fields
- The magnetic field B1 due to coil P (in the XY plane) will be directed along the Z-axis (using the right-hand rule).
- The magnetic field B2 due to coil Q (in the YZ plane) will be directed along the X-axis.
Step 4: Calculate the Magnitude of the Net Magnetic Field
Since B1 and B2 are perpendicular to each other, we can use the Pythagorean theorem to find the resultant magnetic field Bnet:
Bnet=√B21+B22
Substituting the expressions for B1 and B2:
Bnet=
⎷(2π×10−7R)2+(2π√3×10−7R)2
=√(2π×10−7)2R2+(2π√3×10−7)2R2
=2π×10−7R√1+3=2π×10−7R√4=4π×10−7RT
Step 5: Determine the Direction of the Resultant Magnetic Field
The angle θ that the resultant magnetic field makes with B1 can be found using:
tanθ=B2B1=2π√3×10−7R2π×10−7R=√3
Thus,
θ=tan−1(√3)=60∘
Final Answer
The magnitude of the net magnetic field at the center of the coils is:
Bnet=4π×10−7RT
And the direction of the net magnetic field is 60∘ with respect to the magnetic field due to coil P.
The magnetic field B1 at the center of a circular coil is given by the formula:
B1=μ0I12R
where:
- I1=1A (current in coil P)
- μ0=4π×10−7T⋅m/A (permeability of free space)
- R is the radius of the coil (not given, but will cancel out later).
B1=4π×10−7×12R=2π×10−7RT
Similarly, for coil Q, the magnetic field B2 is given by:
B2=μ0I22R
where:
- I2=√3A (current in coil Q).
B2=4π×10−7×√32R=2π√3×10−7RT
- The magnetic field B1 due to coil P (in the XY plane) will be directed along the Z-axis (using the right-hand rule).
- The magnetic field B2 due to coil Q (in the YZ plane) will be directed along the X-axis.
Since B1 and B2 are perpendicular to each other, we can use the Pythagorean theorem to find the resultant magnetic field Bnet:
Bnet=√B21+B22
Bnet=
⎷(2π×10−7R)2+(2π√3×10−7R)2
=√(2π×10−7)2R2+(2π√3×10−7)2R2
=2π×10−7R√1+3=2π×10−7R√4=4π×10−7RT
The angle θ that the resultant magnetic field makes with B1 can be found using:
tanθ=B2B1=2π√3×10−7R2π×10−7R=√3
Thus,
θ=tan−1(√3)=60∘
The magnitude of the net magnetic field at the center of the coils is:
Bnet=4π×10−7RT
And the direction of the net magnetic field is 60∘ with respect to the magnetic field due to coil P.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Test Your Grip (a)1videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Test Your Grip (c)1videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Value Based Questions2videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
- BOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - ASSERTION-REASON TYPE QUESTIONS2videos
ELECTROSTATICS
- BOOK - PRADEEPCHAPTER - OPTICSEXERCISE - Multiple choice questions1videos
OPTICS
Similar Questions
(a) State Biot - Savart law and express this law in the vactor form.
(b) Two identical circular coils, P and Q each of radius R, carrying currents 1A and √3A
respectively, are placed concentrically and perpendicular to each other lying in the XY
and YZ planes. Find the magnitude and direction of the net magnetic field at the centre
of the coils.View SolutionTwo identical circular coils, P and Q each of radius R, carrying currents 1 A and √3 A respectively, are placed concentrically are perpendicualr to each other lying in the XY and YZ planes. Find the magnitude and direction of the net magnetic field at the centre of the coils.
 View Solution
View SolutionTwo small identical circular loops, marked (1) and (2), carrying equal currents are placed with the geometrical axes perpendicular to each other as shown in the fig. Find the fig. Find the magnitude and direction of the net magnetic field at the net magnetic field at the point O.
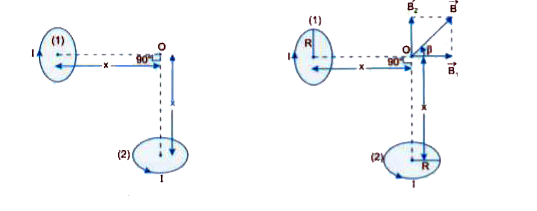 View Solution
View SolutionTwo small circular loops, marked (1) and (2), carrying equal currents are placed with the geometrical axes perpendicular to each other as shown in figure. Find the magnitude and direction of the net magnetic field produced at the point O.
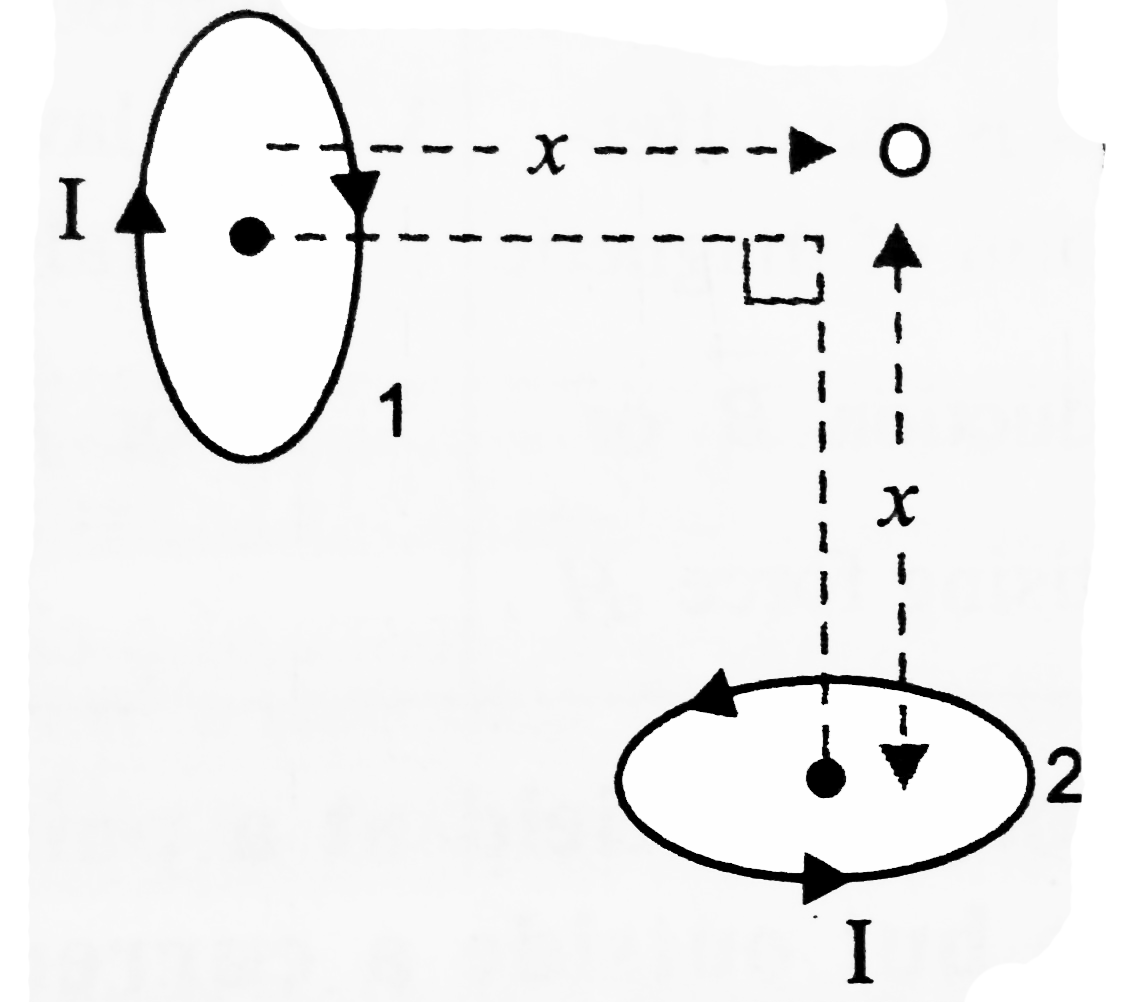 View Solution
View SolutionTwo identical circular wires P and Q each of radius R and carrying current 'I' are kept in perpendicular planes such that they have a common centre as shown in fig. Find the magnitude and direction of the net magnetic field at the common centre of the two coils.
 View Solution
View SolutionTwo identical circular wires P and Q each of radius R and carrying current 'I' are kept in perpendicular planes such that they have a common centre as shown in the figure. Find the magnitude and direction of the net magnetic field at the common centre of the two coils.
 View Solution
View Solution(a) Draw the pattern of magnetic field lines for a circular coil carrying current.
(b) Two identical planes such that they have a common centre at P as shown in the figure. Find the magnitude and direction of the net magnetic field at the point P due to the loopsView Solution(a) Using Biot-Savart's law, derive an expression for the magnetic field at the centre of a circular coil of radius R, number of turns N, carrying current.
(b) Two small identical circular coils marked 1,2 carry equal currents and are placed with their geometric axes perpendicular to each other as shown in the figure. Derive an expression for the resultant magnetic field at O.
 View Solution
View SolutionTwo identical coils P and Q each of radius R are lying in perpendicular planes such that they have a common centre. Find the magnitude and PC direction of the magnetic field at the common centre of the two coils, if they carry currents equal to land √3I respectively.
 View Solution
View SolutionA tightly wound 100 turn coil of radius 10cm is carrying a current of 1A. What is the magnitude of the magnetic field at the centre of the coil?
View Solution

