The M.I. of a circular ring of radius R and mass M about a tangent in its plane is
MR2/2
3/2MR2
MR2
2MR2
The correct Answer is:C
Step by step video, text & image solution for The M.I. of a circular ring of radius R and mass M about a tangent in its plane is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
Moment of inertia of a uniform circular ring of mass M and radius R about a diameter of ring is………………. .
View SolutionThe ratio of the radii of gyration of a circular disc about a tangential axis in the plane of the disc and of a circular ring of the same radius about a tangential axis in the plane of the ring is
View Solution
Knowledge Check
- Question 1 - Select One
The M.I. of a solid sphere of mass 'M' and radius 'R' about a tangent in its plane is
A25MR2B75MR2C23MR2D53MR2 - Question 2 - Select One
The M.I. of a ring of mass M and radius R about a tangential axis perpendicular to its plane is :
A2MR2BMR2C3/2MR2D3/4MR2 - Question 3 - Select One
The ratio of the radii of gyration of a circular disc about a tangential axis in the plane of the disc and of a circular ring of the same radius about a tangential axis in the plane of the ring is
A√3:√5B√12:√3C1:√3D√5:√6
The ratio of the radii of gyration of a circular disc about a tangential axis in the plane of the disc and a circular ring of the same radius about a tengential axis in the plane of the ring is
View SolutionThe moment of inertia of a disc of mass M and radius R about a tangent to its rim in its plane is
View SolutionThe semi circular ring of radius R and mass m is free to rotate about the point O in shown figure.
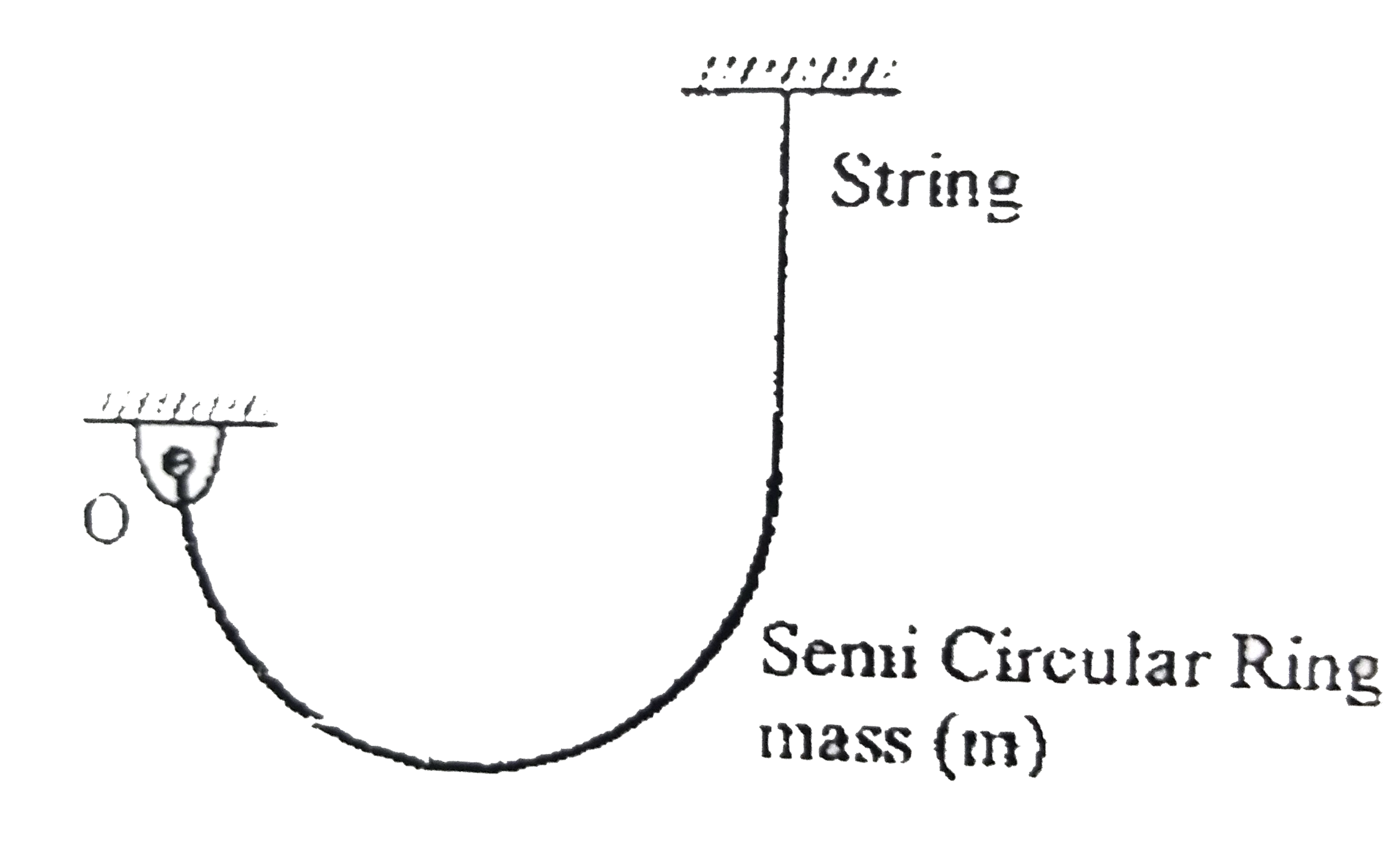 View Solution
View SolutionThe ratio of the radii of gyration of a circular disc about a tangential axis in the plane of the disc and a circular ring of the same radius about a tengential axis in the plane of the ring is
View SolutionThe M.I. of a uniform semicircular disc of mass M and radius R about a line perpendicular to the plane of the disc and passing through the centre is
View Solution

