The semi circular ring of radius R and mass m is free to rotate about the point O in shown figure.
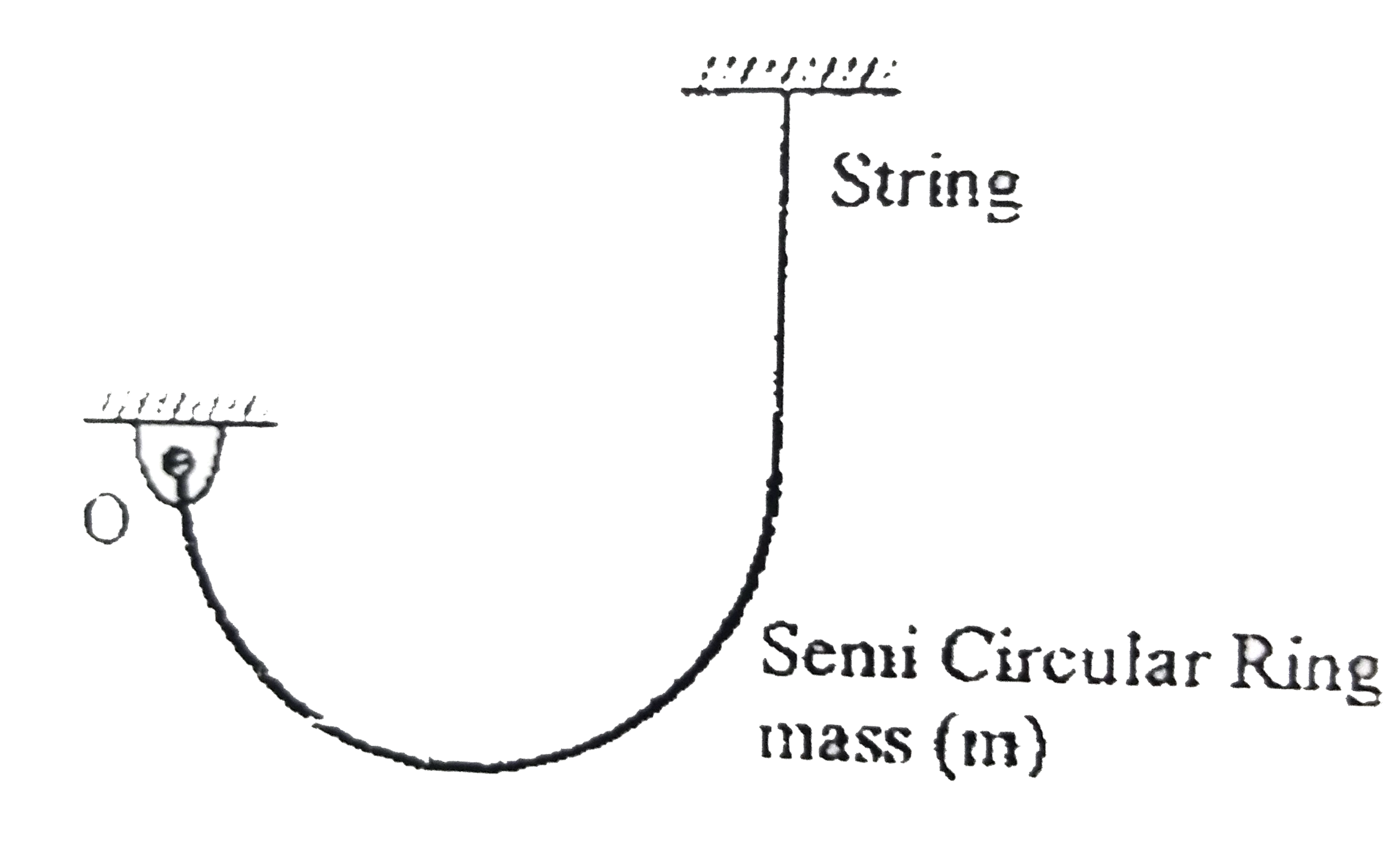
Tension in the string is
Angular acceleration of the semi circular ring just after we cut the string is
Force due to hinge on the semi circular ring always has non zero vetical component
Acceleration of centre of mass of the semi circular ring, just after we cut the string, must have horizontal vertical non zero components.
(A)
(B)
(D) Centre of mass tangential acceleration only.
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)
32 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)
3 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C
4 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
A uniform semi circular ring of mass m is placed on smooth horizontal surface and is free to rotate about an axis passing through point 'O' and perpendicular to the plane of the ring. A particle of same mass is striking the semi circular ring at other end, elastically as shown in the figure. find out angular velocity of the ring just after impact.

View SolutionA conducting circular ring is rotated with angular velocity ω about point A as shown in figure. Radius of ring is a find
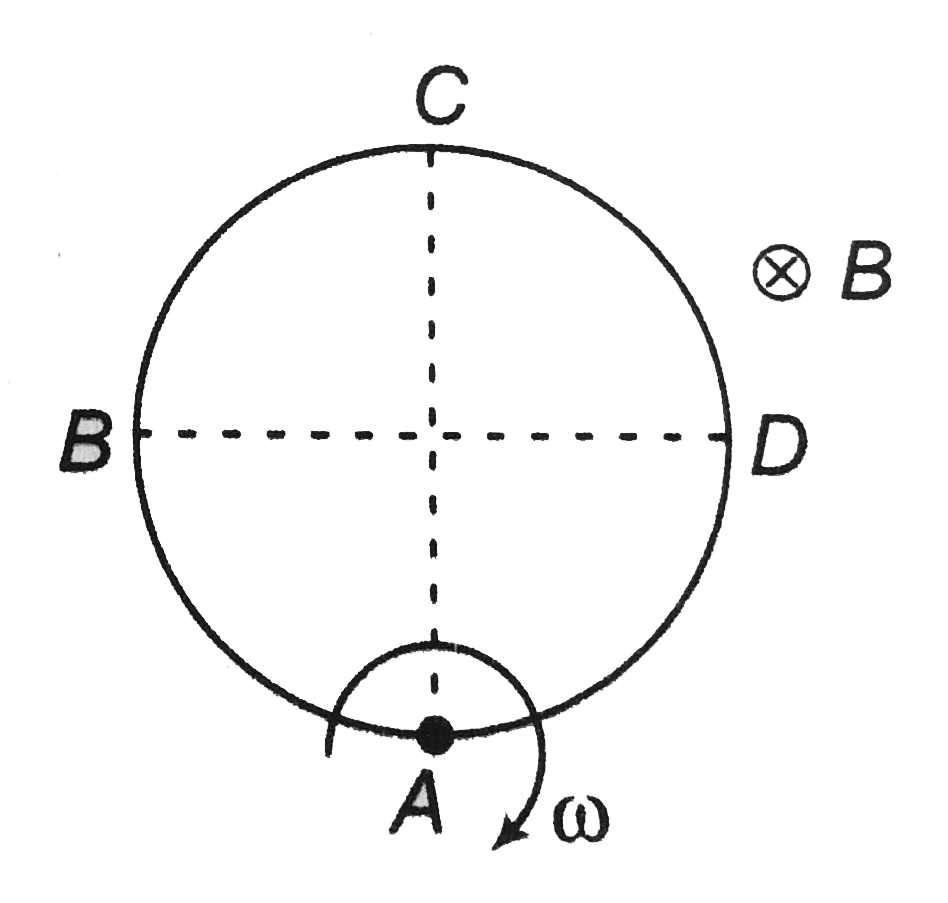
a. potential difference between points A and C
b. potential difference the points A and D.
View Solution
Knowledge Check
A uniform semi circular ring of radius R and mass m is free to oscillate about its one end in its vertical plane as shown in the figure. Find time period of SHM of its centre of mass of the ring (take π2=10)
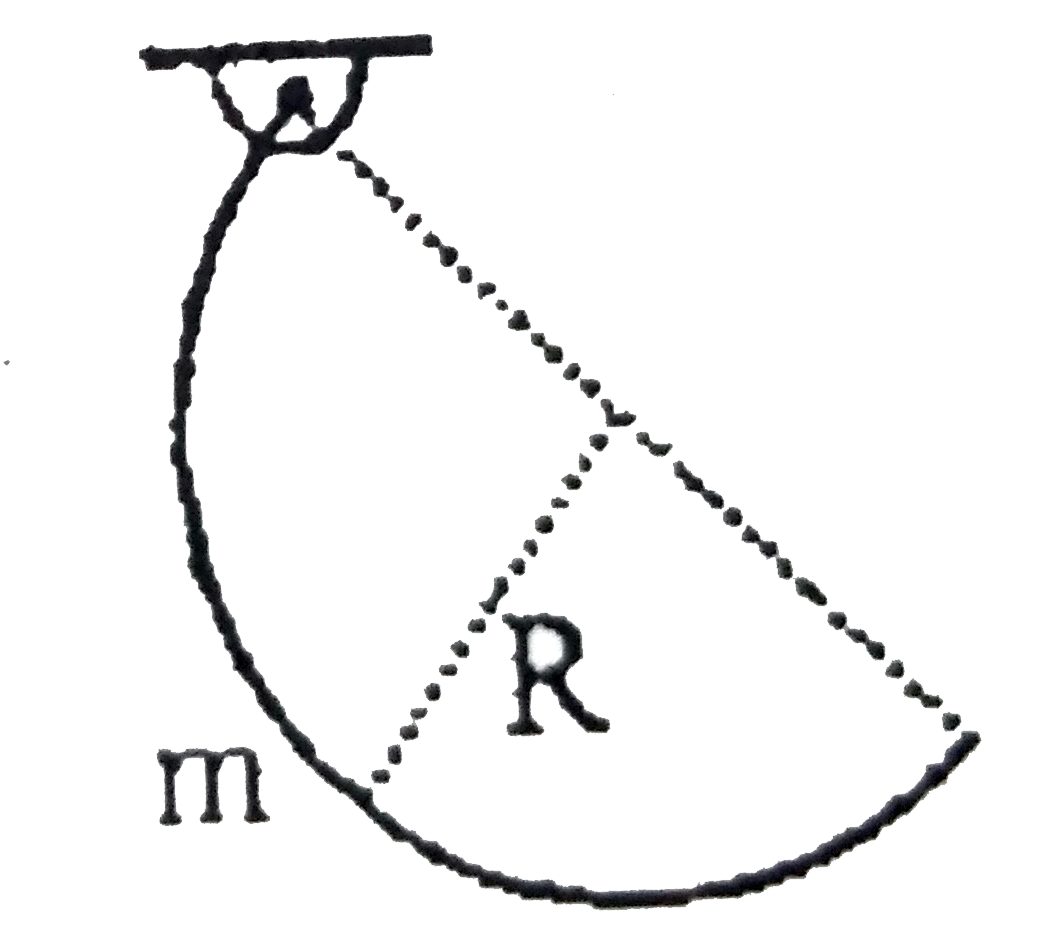 A2π√RgB2π√Rg(√207)C2π√2RgD2π√Rg(145)
A2π√RgB2π√Rg(√207)C2π√2RgD2π√Rg(145)A particle of mass m is placed on centre of curvature of a fixed, uniform semi-circular ring of radius R and mass M as shown in figure. Calculate:
(a) interaction force between the ring and the particle and
(b) work required to displace the particle from centre of curvature to infinity.
 A(a)F=2GMπR2,(b)GMRB(a)F=2GMmπ2R,(b)GMmR2C(a)F=−2GMmπR2(b)−GMmRD(a)F=2GMmπR2(b)GMmR
A(a)F=2GMπR2,(b)GMRB(a)F=2GMmπ2R,(b)GMmR2C(a)F=−2GMmπR2(b)−GMmRD(a)F=2GMmπR2(b)GMmRFrom a uniform circular disc of radius R and mass 9M, a small disc of radius R3 is removed as shown in the figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through centre of disc is :
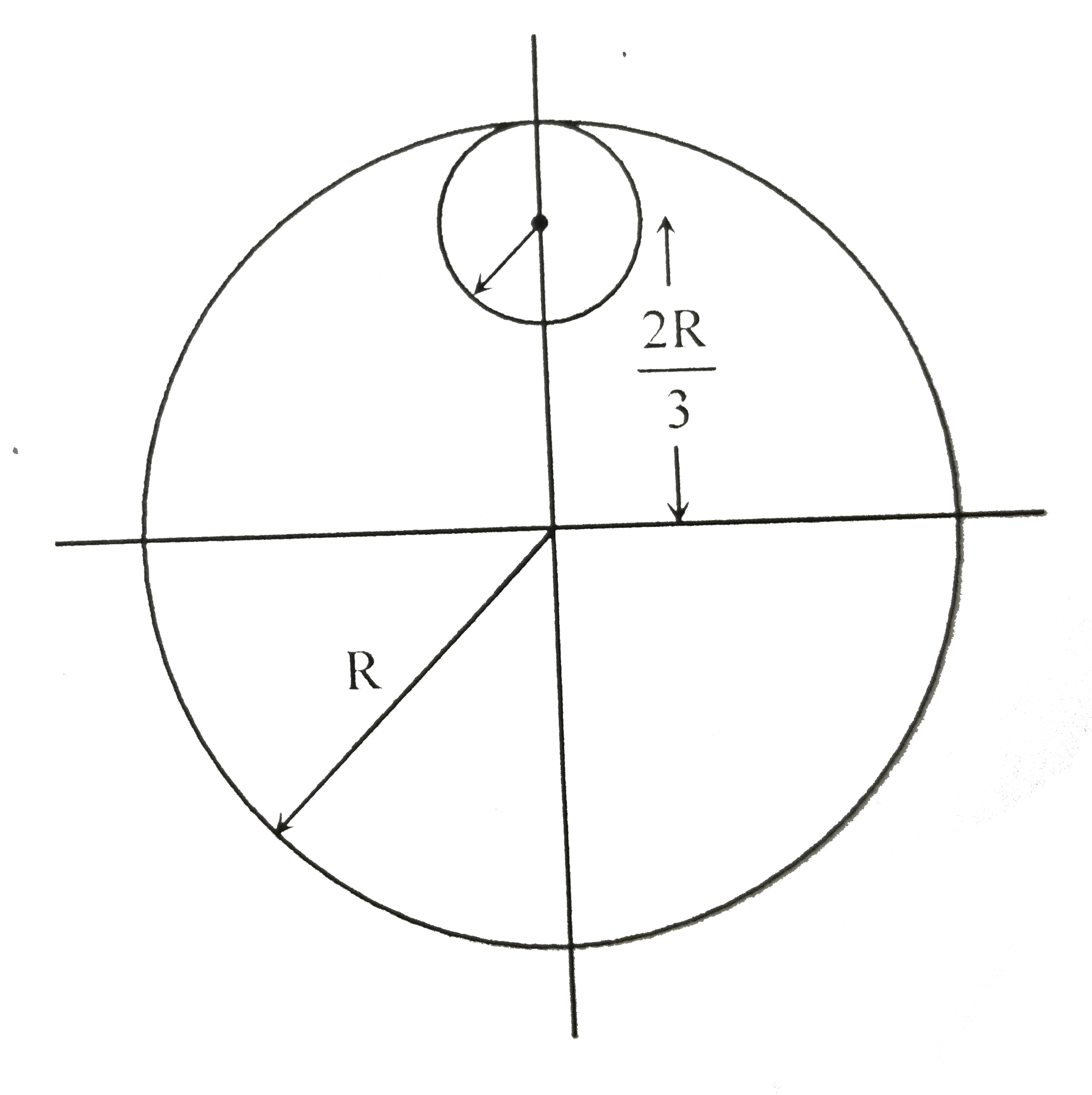 A4MR2B409MR2C40MR2D379MR2
A4MR2B409MR2C40MR2D379MR2
A conducting circular ring is rotated with angular velocity ω about point A as shown in figure. Radius of ring is a find

a. potential difference between points A and C
b. potential difference between the points A and D.
View SolutionFrom a circular disc of radius R and mass 9M, a small disc of radius R/3 is removed as shown in figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is

View SolutionA unifrom solid disk of radius R and mass M is free to rotate on a frictionless pivot through a point on its rim. If the disk is released from rest in the position shown in figure. The speed of the lowest point on the disk in the dashed position is.
 .
.
View SolutionA thin circular ring of mass M and radius r is rotating about its axis with a constant angular velocity ω. Two objects each of mass m are attached gently to the opposite ends of a diameter of the ring. The ring will now rotate with an angular velocity
View SolutionA thin circular ring of mass M and radius r is rotating about its axis with a constant angular velocity ω. Two objects each of mass m are attached gently to the opposite ends of a diameter of the ring. The ring will now rotate with an angular velocity of
View Solution
