The two chords PQ and RS of a circle intersects each other at the point X within the circle. By joining P,S and R,Q prove that ΔPXS and ΔRSQ are similar. From this also prove that PX:XQ=RX:XS.Solution in Bengali
Step by step video & image solution for The two chords PQ and RS of a circle intersects each other at the point X within the circle. By joining P,S and R,Q prove that DeltaPXS and DeltaRSQ are similar. From this also prove that PX: XQ=RX : XS. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMILARITYBOOK - CALCUTTA BOOK HOUSECHAPTER - SIMILARITYEXERCISE - Exercise 5.1
32 Videos
- SIMILARITYBOOK - CALCUTTA BOOK HOUSECHAPTER - SIMILARITYEXERCISE - Exercise 5.2
27 Videos
- SAMPLE QUESTIONS PAPERSBOOK - CALCUTTA BOOK HOUSECHAPTER - SAMPLE QUESTIONS PAPERSEXERCISE - QUESTION
157 Videos
- SIMPLE INTERESTBOOK - CALCUTTA BOOK HOUSECHAPTER - SIMPLE INTERESTEXERCISE - Long-answer type questions
37 Videos
Similar Questions
In the following figure , ∠P=
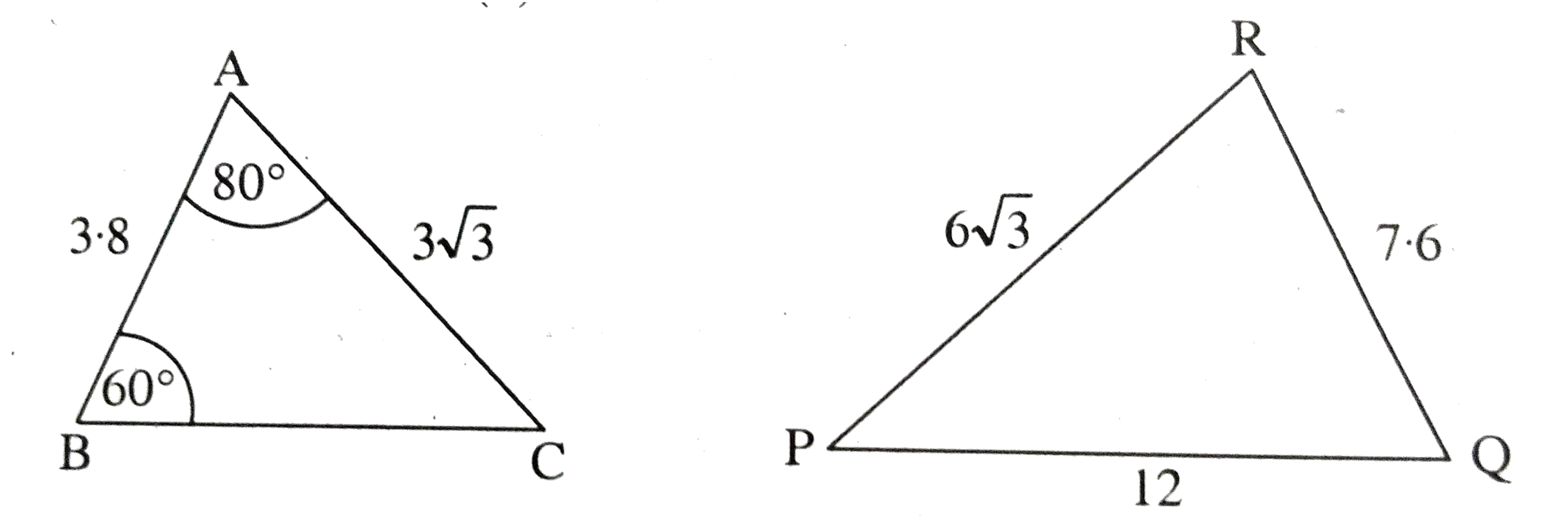
View SolutionIn ΔPQR and ΔDEF, PQDE=QREF=RPFD. Then which one of the following is correct?
View SolutionA person deposite ₹ 100 in a bank and after 2 yars he got a total ₹121 as a return. Then the componund interest of the bank per annum is
View SolutionGoutam took a loan of some money from a cooperative bank for opening a poultry farm at the rate of simple interest of 12% per annum. Every month he has to repay 378Rs as interest. Determine the loan amount taken by him.
View SolutionIf two equal chords of a circle intersect within the circle, prove that the segments ofone chord are equal to corresponding segments of the other chord.
View SolutionIf two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the center makes equal angles with the chords.
View SolutionTwo circles intersect each other at the points G and H . A straight line is drawn through the point G which intersect two circles at the points P and Q and the straight line through the point H parallel to PQ intersects the two circles at the points R and S . Prove that PQ=RS .
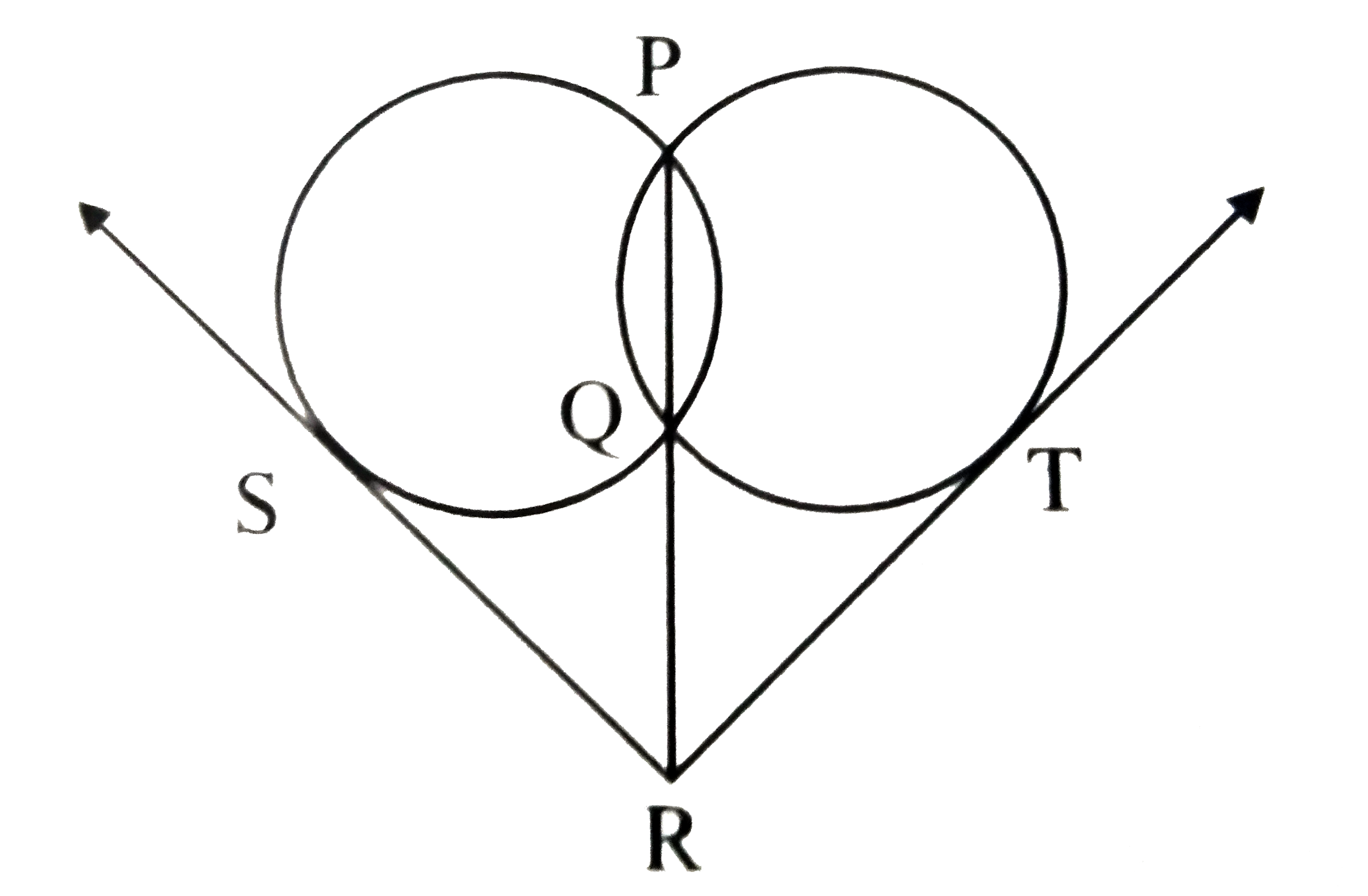
View SolutionIn the figure, two circles intersect each other in points P and Q. If tangent from point R touch the circles at S and T, then prove that RS=RT.
View SolutionIf two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.
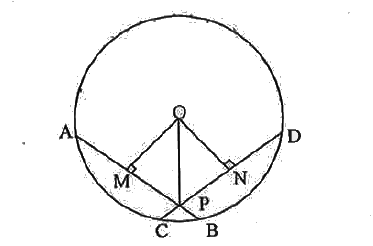
View SolutionIf two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
View SolutionIf two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
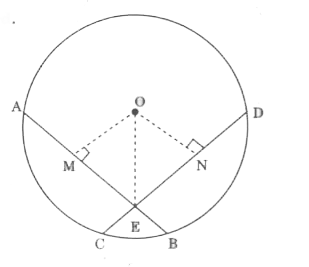
View SolutionIf two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.
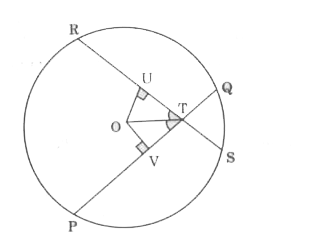
View SolutionIf two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
View SolutionIf two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.
View SolutionSumita draws two circles which intersect each other at point O. If PQ and RS are the diameters of two circles which are parallel to each other, then prove that the points P, O and S are three isosceles.
View Solution
