Take any point O in the interior of a triangle PQR. Is (i) OP+OQ>PQ? (ii) OQ+OR>QR? (iii) OR+OP>RP?
To solve the problem, we need to analyze the relationships between the sides of triangle PQR and the segments connecting point O (which is inside the triangle) to the vertices P,Q, and R.
1. Understanding the Triangle and Point O:
- We have a triangle PQR and a point O located inside this triangle.
- We will draw segments from point O to each of the vertices P,Q, and R, creating segments OP,OQ, and OR.
2. Analyzing Triangle OPQ:
- Consider triangle OPQ.
- According to the triangle inequality theorem, the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
- Therefore, we can state:
OP+OQ>PQ
- This confirms that the first part is true.
3. Analyzing Triangle OQR:
- Next, consider triangle OQR.
- Again applying the triangle inequality theorem:
OQ+OR>QR
- This confirms that the second part is also true.
4. Analyzing Triangle POR:
- Finally, consider triangle POR.
- Using the triangle inequality theorem once more:
OP+OR>RP
- This confirms that the third part is also true.
Conclusion:
All three statements are true:
1. OP+OQ>PQ
2. OQ+OR>QR
3. OR+OP>RP
- We have a triangle PQR and a point O located inside this triangle.
- We will draw segments from point O to each of the vertices P,Q, and R, creating segments OP,OQ, and OR.
- Consider triangle OPQ.
- According to the triangle inequality theorem, the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
- Therefore, we can state:
OP+OQ>PQ
- This confirms that the first part is true.
- Next, consider triangle OQR.
- Again applying the triangle inequality theorem:
OQ+OR>QR
- This confirms that the second part is also true.
- Finally, consider triangle POR.
- Using the triangle inequality theorem once more:
OP+OR>RP
- This confirms that the third part is also true.
All three statements are true:
1. OP+OQ>PQ
2. OQ+OR>QR
3. OR+OP>RP
Topper's Solved these Questions
- BOOK - NCERT ENGLISHCHAPTER - THE TRIANGLE AND ITS PROPERTIESEXERCISE - EXERCISE 6.58videos
THE TRIANGLE AND ITS PROPERTIES
- BOOK - NCERT ENGLISHCHAPTER - THE TRIANGLE AND ITS PROPERTIESEXERCISE - EXERCISE 6.11videos
THE TRIANGLE AND ITS PROPERTIES
- BOOK - NCERT ENGLISHCHAPTER - THE TRIANGLE AND ITS PROPERTIESEXERCISE - SOLVED EXAMPLES6videos
THE TRIANGLE AND ITS PROPERTIES
- BOOK - NCERT ENGLISHCHAPTER - SYMMETRYEXERCISE - EXERCISE 14.22videos
SYMMETRY
Similar Questions
A point A is inside a triangle PQR. Show that 2(AP+AQ+AR)>PQ+QR+RP.
View SolutionO is any point in the interior of a triangle ABC.
Prove that :
OB+OC<AB+AC.
 _Q01.png" width="60%">View Solution
_Q01.png" width="60%">View SolutionS is any point on side QR of a ΔPQR. Show that PQ+QR+RP>2PS .
View SolutionIn Figure, PQR is a triangle and S is any point in its interior, show that SQ+SR<PQ+PR. Given : S is any point in the interior of PQR To Prove : SQ+SR<PQ+PR Construction: Produce QS to meet PR in T
View SolutionIn Fig., which of the following statements are true: (i) Point B is the interior of ∠AOB (ii) Point B is the interior of ∠AOC (iii)Point A is the interior of ∠AOD (iv)point C is the exterior of ∠AOB (v)Point D is the exterior of ∠AOC.
View SolutionConstruct a triangle PQR, in which PR=6cmandPQ=QR=6.8cm.
Mark S the mid-point of PQ.View SolutionA and B are respectively the points on the sides PQ and PR of a ΔPQR such that PQ =12.5 cm, PA= 5 cm, BR = 6 cm and PB = 4 cm. Is AB || QR? Give reason for your answer.
View SolutionIn the given figure , CM and RN are respectively the median of triangles ABC and PQR

IF ΔABC is similar to ΔPQR ,prove that
(i) ΔAMC~ΔPNR
(ii) CMRN=ABPQand
(iii)ΔCMB~ΔRNQView SolutionIn the given figure, ABCD is a square and ∠PQR=90∘.IfPB=QC=DR, prove that.
(i) QB = RC
(ii) PQ = QR
(iii) ∠QPR=45∘
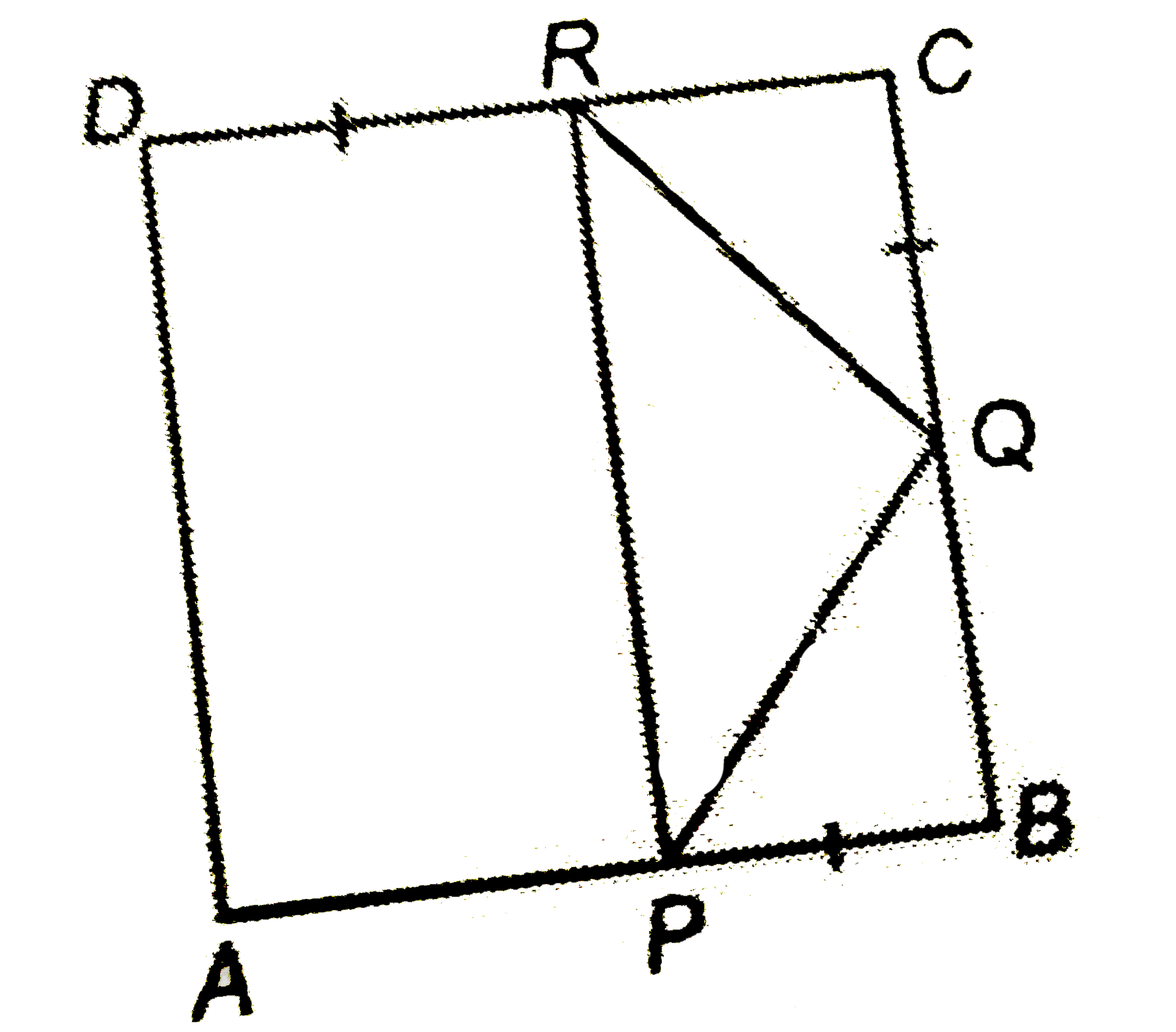 View Solution
View SolutionAngles QandR of a ΔPQR are 25∘and65∘. Write which of the following is true : (i) PQ2+QR2=RP2 (ii) PQ2+RP2=QR2 ( iii) RP2+QR2=PQ2
View Solution

