In the given figure, are shown two arcs PAQ and PBQ. Arc PAQ is a part of circle with centre O and radius OP while are PBQ is a semi-circle drawn on PQ as diameter with centre M. If PQ = OP = 10 cm show that area of shaded region is 25(√3−π6).
area of semicircle PBQ - area of segment PAQ
Area of semicircle= πr22
=π×252cm2
area of segment PAQ = Area of arc POQ - Area of
Tri POQ
360∘→πr2
1∘→πr2360
60∘→60360×πr2
=16×π×100−√34×100
=100(π6−√34)cm2
=25π2−100π6+100√34
=75π−100π6+25√3
=−25π6+25√3
Answer
Similar Questions
In the given figure, are shown two arcs PAQ and PBQ. Arc PAQ is a part of circle with centre O and radius OP while are PBQ is a semi-circle drawn on PQ as diameter with centre M. OP=PQ=10 cm show that area of shaded region is 25(√3−π6)cm2
View SolutionThe diagram shown two arcs, A and B. Arc A is part of the circle with centre O and radius OP . Arc B is part of the circle with centre M and radius PM , where is the mid-point of PQ. Show that the area enclosed by the two arcs is equal to 25(√3−π6)cm2
View Solution
Knowledge Check
In the given figure, ABCD is a square with side 10 cm. BFD is an arc of a circle with centre C and BGD is an arc of a circle with centre A. What is the area of the shaded region in square centimetres ?
 A100−50πB100–25πC50π−100D25π–100
A100−50πB100–25πC50π−100D25π–100
In the given figure, AB and PQ are perpendicular diameters of the circle whose centre is O and radius OA = 7 cm. Find the area of the shade region.

View SolutionIn the given figure, AB and PQ are perpendicular diameters of the circle whose centre is O and radius OA = 7 cm. Find the area of the shade region.

View SolutionPS is the diameter of a circle of radius 6 cm. The points Q and R cts the diameter Ps. Semi circles are drawn on PQ and Qs as diameters. Find the area of the shaded region.
View SolutionIn the figure, PQ is tangent to a circle with centre O. OQ=12, PQ=6. Find the area of the shaded portion

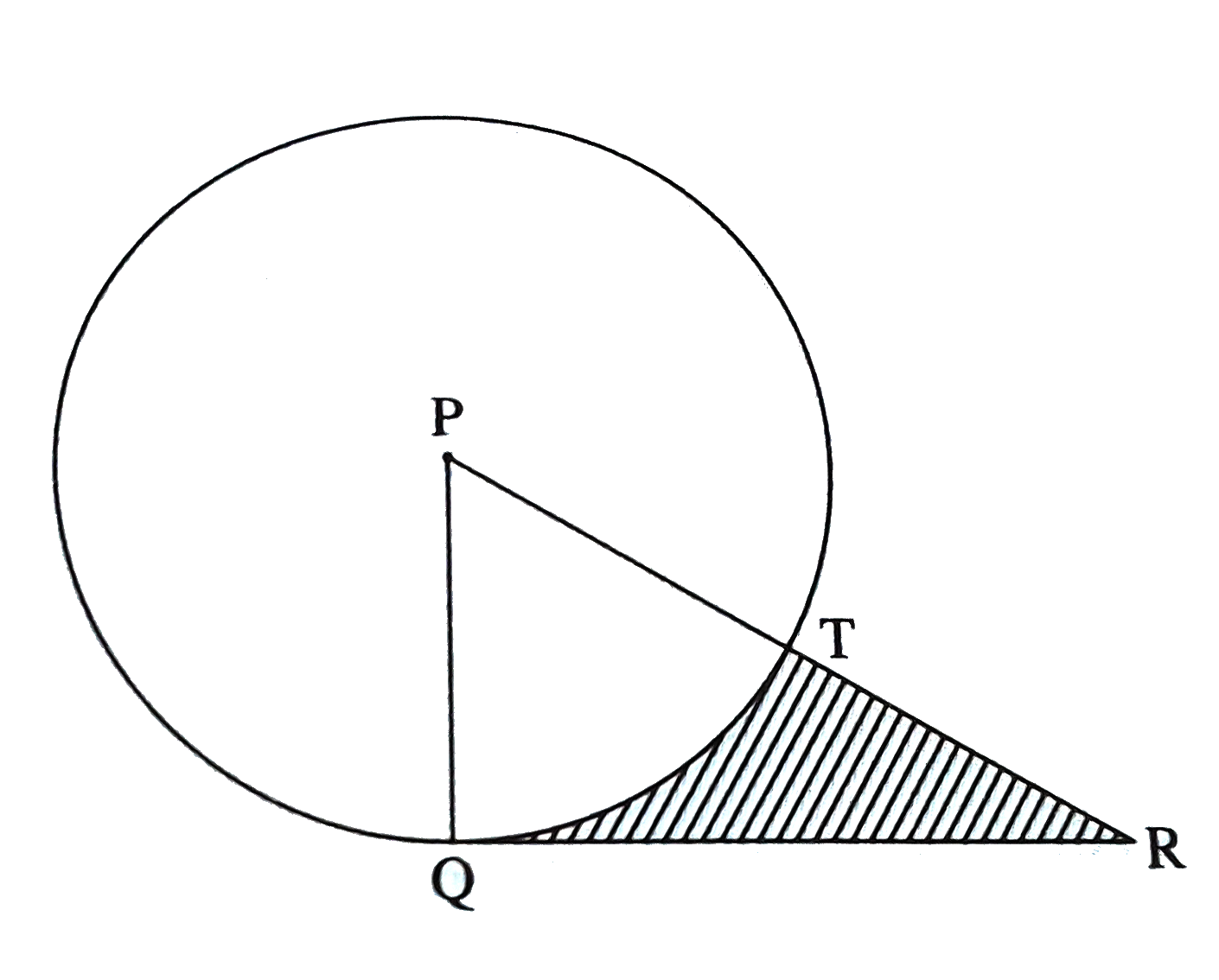
View SolutionIn the figure, segment QR is a tangent to the circle with centre P.PR = 12 cm and PQ = 6 cm. Find the area of shaded region. (√3=1.73,π=3.14)
View SolutionIn figure ABDC is a quadrant of a circle of a radius 28 cm and a semi circles BEC is drawn with BC as diameter find the area of shaded region:
View SolutionIn the figure, O is the centre of the circle.
m(arc PQR)=60∘
OP = 10 cm.
Find the area of the shaded region. (π=3.14,√3=1.73)

View Solution
