A conducting ring of radius a is rotated about a point O on its periphery as shown in the figure in a plane perpendicular to uniform magnetic field B which exists everywhere. The rotational velocity is omega.

Choose the correct statement(s) related to the potential of the points P, Q and R
VP−VO>0andVR−VO<0
VP=VR>VO
VO>VP=VQ
VQ−VP=VP−VO
The correct Answer is:B, D
VP−VO=VR−VO=12Bω(√2a)2
VP−VO=VR−VO=Bωa2
VP=VR>VO

VQ−VP=(VQ−VP)−(VP−VO)
=12Bω(2a)2−(12Bω(√2a)2)=Bωa2
=VQ−VP=VP−VQ
Similar Questions
A conducting rod AB of length l is rotated about point O with an angular velocity velocity omega in a uniform magnetic field (B_0) directed perpendicular into the plane of rotation as shown in the figure. The value of VB−VA is
View SolutionThere is a ring or mass m and radius R is pivoted at a point O on its periphery. It is free to rotate about an axis perpendicular to its plane. What is the period of ring?
View Solution
Knowledge Check
A conducting ring of radius a is rotated about a point O on its periphery as shown in the figure in a plane perpendicular to uniform magnetic field B which exists everywhere. The rotational velocity is omega.

Choose the correct statement(s) related to the induced current in the ringACurrent flows from Q→P→O→R→QBCurrent flows from Q→R→O→P→QCCurrent flows from Q→P→OandomQ→R→ODNo current flowsA conducting ring of radius a is rotated about a point O on its periphery as shown in the figure in a plane perpendicular to uniform magnetic field B which exists everywhere. The rotational velocity is omega.

Choose the correct statement(s) related to the magnitude of potential differencesAVP−VO=12Bωa2BVP−VQ=12Bωa2CVQ−VO=2Bωa2DVP−VR=2Bωa2A non-conducting disk of radius R is rotating about its own axis with constant angular velocity ω in a perpendicular uniform magnetic field B as shown in figure. The emf induced between centre and rim of disk is
 ABωR22BBωR2CZeroDBωR23
ABωR22BBωR2CZeroDBωR23
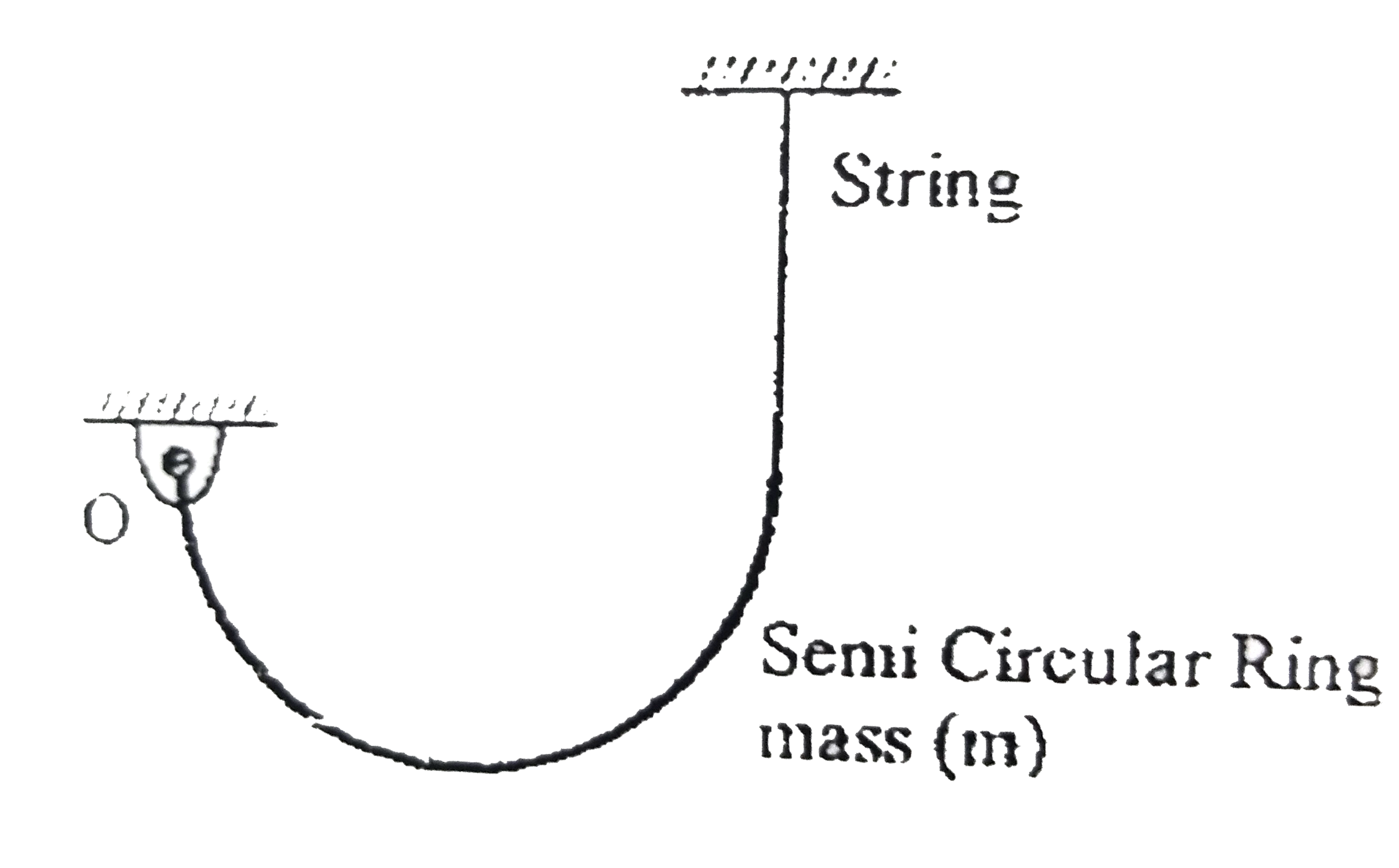
The semi circular ring of radius R and mass m is free to rotate about the point O in shown figure.
View SolutionA conducting rod rotates with a constant angular velocity 'ω' about the axis which passes through point 'O' and perpendicular to its length . A uniform magnetic field 'B' exists parallel to the axis of the rotation . Then potential difference between the two ends of the rod is :-
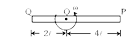
View SolutionA conducting ring of radius 2R rolls on a smooth horizontal conducting surface as shown in figure-5.295. A uniform horizontal magnetic field B is perpendicular to the plane of the ring. The potential of A with respect to O is:

View SolutionA circular metal plate of radius R is rotating with a uniform angular velocity ω with its plane perpendicular to a uniform magnetic field B. Then the emf developed between the centre and the rim of the plate is :
View SolutionA circular metal plate of radius R is rotating with a uniform angular velocity ω with its plane perpendicular to a uniform magnetic field B. Then the emf developed between the centre and the rim of the plate is :
View Solution
