ABC is an isoceless triangle in which AB= AC. AD bisects exterior ∠PAC and CD||AB. Show that (i) ∠DAC=∠BCA (ii) ABCD is a plarallelogram.
Step by step video & image solution for ABC is an isoceless triangle in which AB= AC. AD bisects exterior /_PAC and CD||AB. Show that (i) /_DAC = /_BCA (ii) ABCD is a plarallelogram. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Similar Questions
ABC is an isoceless triangle in which AB= AC. AD bisects exterior ∠PAC and CD||AB. Show that (i) ∠DAC=∠BCA (ii) ABCD is a plarallelogram.
View SolutionABC is an isosceles triangle in which AB=AC. AD bisects exterior angle PAC and CD∣∣AB. Show that(i) ∠DAC=∠BCA and (ii) ABCD is a parallelogram.
View SolutionABC is an isosceles triangle in which AB = AC . AP bisects exterior angle DAC and CP II AB . Show that angle PAC = Angle BCA (ii) ABCP is a Parallelogram
View SolutionABC is an isosceles triangle in which AB=AC. AD bisects exterior angle PAC and CD∣∣AB. Show that(i) ∠DAC=∠BCA and (ii) ABCD is a parallelogram.
View SolutionAD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
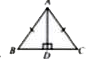
AD bisects BC
View SolutionAD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
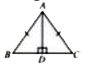
AD bisects ∠A
View SolutionABC is a triangle in which ∠B=∠C and ray AX bisects the exterior angle DAC . If ∠DAX=700 find ∠ACB.
View SolutionABC is a triangle in which ∠B=2∠C.D is a point on BC such that AD bisects ∠BAC and AB=CD. Prove that ∠BAC=72∘
View SolutionABC is a triangle in which AB = AC and D is any point on BC. Prove that:
AB2−AD2=BD.CD
View SolutionABCD is a quadrilateral in which AB=BC and AD =CD ,Show that BD bisects boht the angle ABC and ADC
View Solution
