MNOP is a parallelogramm as shown in the figure X is any point on MO RQ∣∣MN and BS∣∣PM show that ar(PSXR)=ar(BNQX)
PSXR is a parallelogram
SOQX is a parallelogram
BNQX is a parallelogram
RXBM is a parallelogram
ar(∠MOP)=ar(∠MNP)
InRXBM:a=d
ar(∠MRX)=ar(∠MBX)
In∠SOQM
ar(∠XSO)=ar(XQO)
a+b+c=d+e+f
c=f
ar(PSXR)=ar(BNQX)
From diagram
a+b+c=a+b+a
c=d.
Hence proved.
Similar Questions
The area of the triangle with vertices (a,b),(ar,bs),(ar2,bs2) is
View SolutionIN the figure, P is a point in the interior of a parallelogram ABCD. Show that
(i) ar(APB) + ar(PCD) = 12 ar (ABCD)
(ii) ar (APD) + ar(PBC) = ar(APB) + ar (PCD)
View SolutionIN given figure, PQRS and ABRS are parallelograms and X is any point
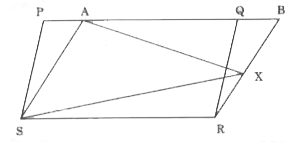
(i) ar (PQRS) = ar (ABRS)
(ii) ar (AXS) = 1/2 ar (PQRS)
View SolutionIn the Given figure, E is any point on median AD of a △ABC Show that ar (ABE) = ar (ACE)
View SolutionIn the figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that ar(PQRS) = ar(ABRS)
View SolutionIn the figure, E is any point on median AD of a triangleABC . Show that ar( triangleABE )= ar( triangleACE ).
View SolutionIn the figure. ABCD is a parallelogram and O is any point on BC . Prove that ar (triangleABO) + ar (triangleDOC) = ar(triangleODA)
View SolutionPQRS is a ||gm. L is any point on PS and M is any point on QR. Show that: ar(triangleQLR) = ar(triangleQPM) + ar(triangleSRM)
View Solution
