Find the law according to which the mass of the rocket varies with time, when the rocket moves with a constant acceleration w, the external forces are absent, the gas escapes with a constant velocity u relative to the rocket, and its mass at the initial moment equals m0.
According to the question, →F (external force) =0
So, md→vdt=dmdt→u
As d→v↑↓→u,
so, in scalar form, mdv=−udm
or, wdtu=−dmm
Integrating within the limits for m(t)
wtu=−m∫m0dmm or, vu=−1nmm0
Hence, m=m0e−(wt/u)
Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Universal Gravitation
34 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Dynamics Of A Solid Body
56 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - The Fundamental Equation Of Dynamics
59 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena
38 Videos
Similar Questions
Find the mass of the rocket as a function of time, if it moves with a constant acceleration a, in absence of external forces. The gas escapes with a constant velocity u relative to the rocket and its mass initially was m0.
View SolutionA relativistic rocket emits a gas jet with non-relativistic velocity u constant relative to the rocket. Find how the velocity v of the rocket depends on its rest mass m if the initial rest mass of the rocket equals to m0.
View Solution
Knowledge Check
A particle of mass m is moving along the line y-b with constant acceleration a. The areal velocity of the position vector of the particle at time t is (u=0)
AconstantBabt2Cabt2mDa2bt2mIf M is mass of rocket, r is rate of ejection of gases and u is velocity of gases with respect to rocket then acceleration of the rocket dv/dt is equal to
AruM−rtBM−rtruCruM+rtDruMAs shown in the figure a block of mass 'm' is placed on a smooth wedge moving with constant acceleration such that block does not move with respect to the wedge. Find work done by the net force on the block in time t. (Initial speed is 0)
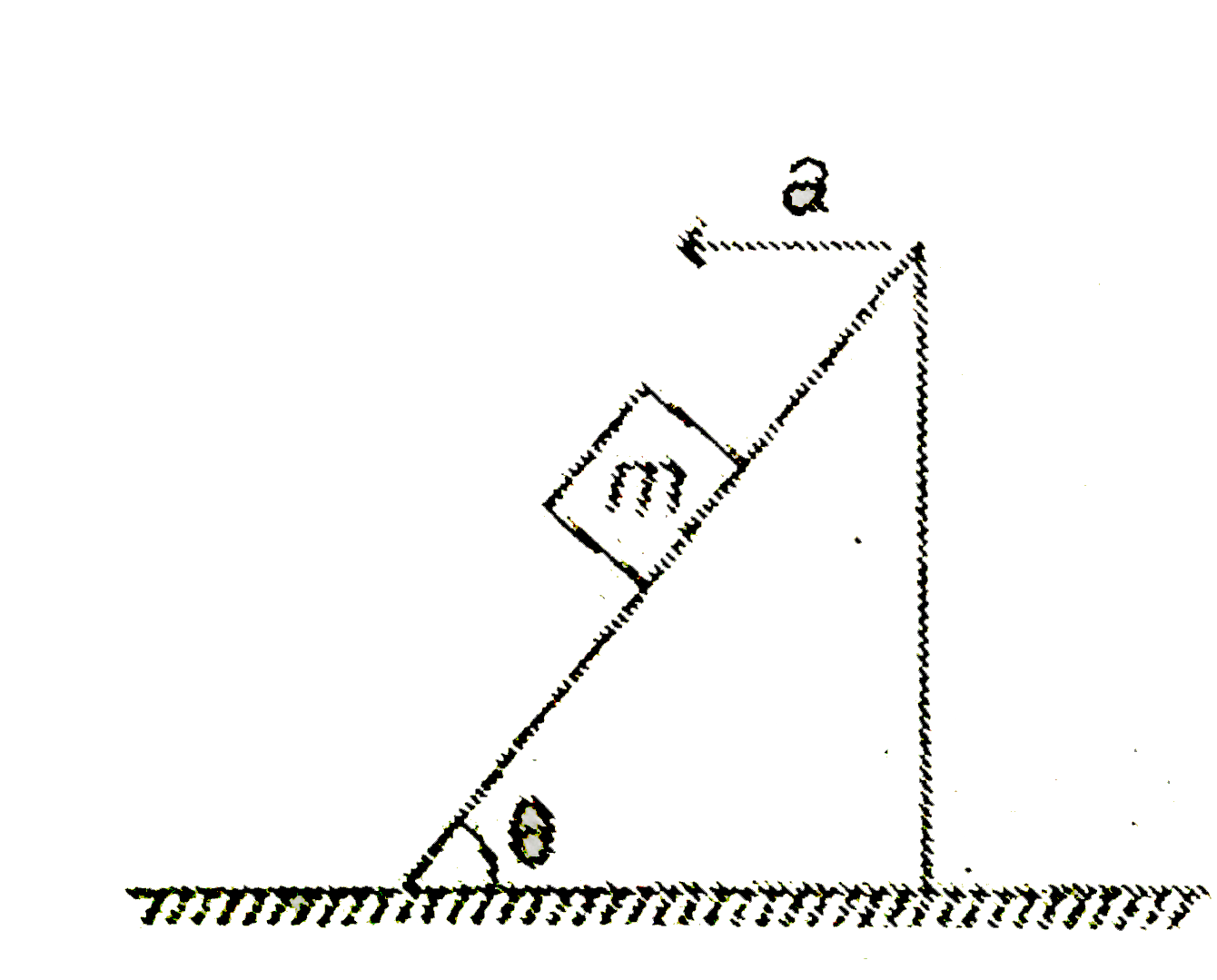 Am(gttanθ)2Bm3(gttanθ)2C49m(gttanθ)2Dm2(gttanθ)2
Am(gttanθ)2Bm3(gttanθ)2C49m(gttanθ)2Dm2(gttanθ)2
A cart loaded with sand moves along a horizontal plane due to a constant force F coinciding in direction with the cart's velocity vector. In the process, sand spills through a hole in the bottom with a constant velocity μkg/s. Find the acceleration and the velocity of the cart at the moment t, if at the initial moment t=0 the cart with loaded sand had the mass m0 and its velocity was equal to zero. The friction is to be neglected.
View SolutionA prototype of a rocket is fired from the ground. The rocket rises vertically up with a uniform acceleration of 54m/s2. 8 second after the start a small nut gets detached from the rocket. Assume that the rocket keeps rising with the constant acceleration.
(a) What is the height of the rocket at the instant the nut lands on the ground
(b) Plot the velocity – time graph for the motion of the nut after it separates from the rocket till it hits the ground. Plot the same velocity– time graph in the reference frame of the rocket. Take vertically upward direction as positive and g=10m/s2
View SolutionA rocket is fired vertically from the ground. It moves upwards with a constant acceleration 10m/s2 after 30 sec the fuel is finished. After what time from the instant of firing the rocket will attain the maximum height? g=10m/s2:-
View SolutionA particle moves rectilinearly with initial velocity u and constant acceleration a. Find the average velocity of the particle in a time interval from t=0 to t=t second of its motion.
View SolutionA double stage rocket has an initial mass Mi, gas is exhausted front he rocket at a constant rate of dm/dt and with an exhaust velocity u relative to the rocket. When the mass of the rocket reaches the value μ, the first stage of mass m of
Which fuel is exhausted is disengaged from the rocket and then the rocket continues to the second stage at teh same rate and exhaust velocity as int eh first stage, until it reaches a mass Mf
(a). Calculate the rocket velocity at the end of the first stage, given that it is started at rest.
(b). Calculat ethe rocket velocity at the end of the second stage. ltbr> (c). What is the final velocity of a one stage rocket of the same initial Mi mass and the same amount of fuel ? it is greater or less than final velocity of the double stage rocket?
View Solution
