A small body of mass m tied to a non-stretchable thread moves over a smooth horizontal plane. The other end of the thread is being drawn into a hole O(figure) with a constant velocity. Find the thread tension as a function of the distance r between the body and the hole if at r=r0 the angular velocity of the thread is equal to ω0.
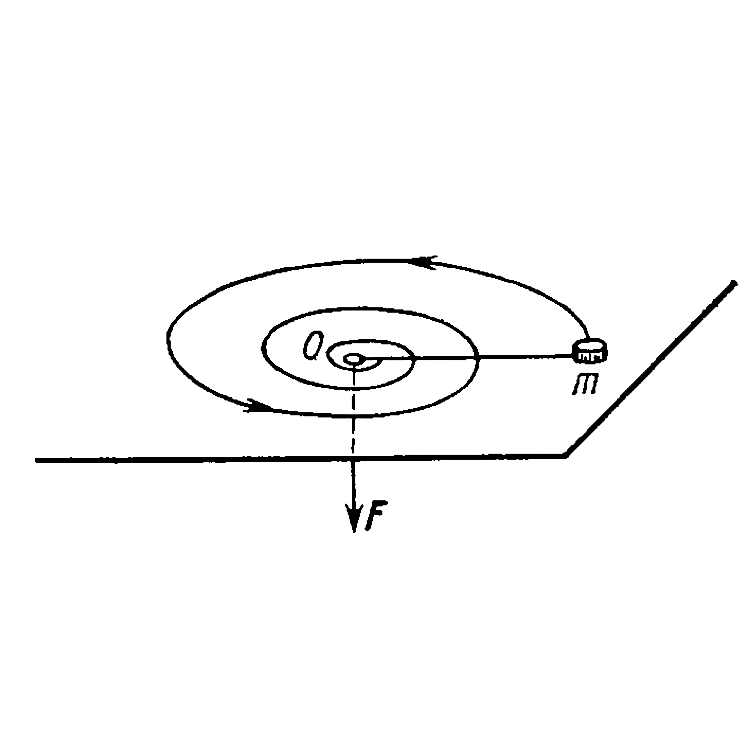
Forces, acting on the mass m are shown in the figure. As →N=m→g, the net torque of these two forces about any fixed point must be equal to zero. Tension T, acting on the mass m is a central force, which is always directed towards the centre O. Hence the moment of force T is also zero about the point O and therefore the angular momentum of the particle m is conserved about O.
Let, the angular velocity of the particle be ω, when the separation between hole and particle m is r, then from the conservation of momentum about the point O, :
m(ω0r0)r0=m(ωr)r,
or ω=ω0r20r2
Now, from the second law of motion for m,
T=F=mω2r
Hence the sought tension,
F=mω20r40rr4=mω20r40r3

Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Universal Gravitation34videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Dynamics Of A Solid Body56videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - The Fundamental Equation Of Dynamics59videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation36videos
OSCILLATIONS AND WAVES
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena38videos
THERMODYNAMICS AND MOLECULAR PHYSICS
Similar Questions
Figure shows s small mass m hanging over a pulley. The other end of the thread is being pulled in horizontal direction with a uniform speed u. Find the speed with which the mass ascend at the instant the string makes an angle θ with the horizontal.
 View Solution
View SolutionA body of mass m s connected to an inextensible thread of length L si whirled in horizontal circle. Find the maximum angular velocity with which it can be whirsted without breaking the thread (Breaking stress of thread =S)
View Solution
Knowledge Check
- Question 1 - Select One
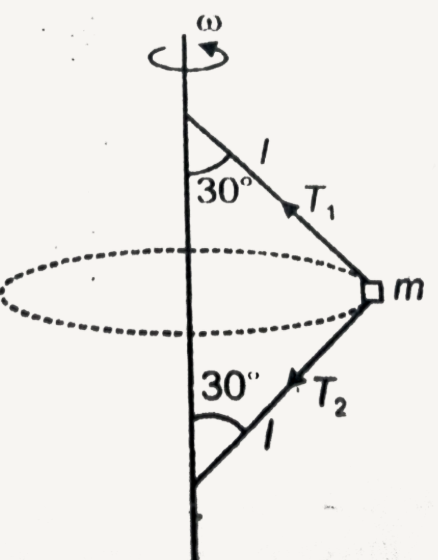
A particle of mass m is whirled in horizontal circle with the help of two threads of length l each as shown in figure . Angular velocity equals ω, then
T1 equalsAmg√3+mω2l2Bmg√3+mω2l2Cmω2l2Dmg√3
A small sphere of mass m suspended by a thread is first taken aside so that the thread forms the right angle with the vertical and then released. Find:
(a) the total acceleration of the sphere and the thread tension as a function of θ, the angle of deflection of the thread from the vertical,
(b) the thread tension at the moment when the vertical component of the sphere's velocity is maximum,
(c) the angle θ between the thread and the vertical at the moment when the total acceleration vector of the sphere is directed horizontally.View SolutionA ring of mass m and radius R is being rotated about its axis with constant angular velocity ω in the gravity free space. Find tension in the ring.
View SolutionA closed chian A of mass m=0.36kg is attached to a vertical rotating shaft by means of a thread (figuer), and rotates with a constant angular velocity ω=35rad/s. The thread forms an angle θ=45∘ with the vertical. Find the distance between the chain's of the thread.
 View Solution
View SolutionA particle of mass m is whirled in horizontal circle with the help of two threads of length l each as shown in figure . Angular velocity equals ω, then
 View Solution
View Solutiona small sphere of mass m susopended by a thread is first taken aside so that the thread forms the right angle with the verticle and then realease. (a) find the total acceleration of the sphere and the thread tension as a function of θ, the angle of deflection of the thread from the vertical. (b) Find the angle θ between the thread and the vertical. at the moment when the total acceleration vector of the sphere is directed (i) horizontally (ii)vertically upward and (iii) vertically downward.
View SolutionA horizontally oriented uniform disc of mass M and radius R rotates freely about a stationary vertical axis passing through its centre. The disc has a radial guide along which can slide without friction a small body of mass m. A light thread running down through the hollow axle of the disc is tied to the body initially the body was located at the edge of the disc and the whole system rotated with ann angular velocity ω0. Then by means of a force F applied to the lower and of the thread the body was slowly pulled to the rotation axis. find:
(a). The angular velocity of the system in its final state.
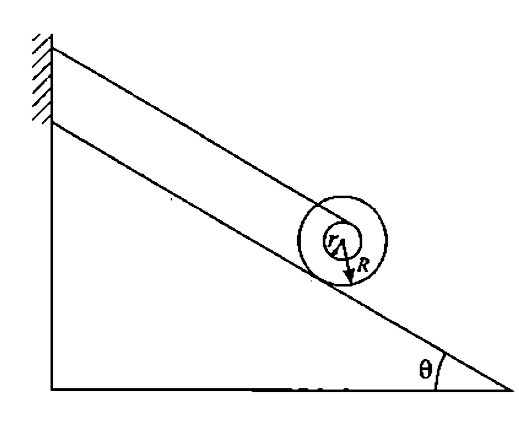
(b). The work performed by the force F.View SolutionA spool of thread of mass m is placed on an inclined smooth plane set at an angleθ to the horizontal. The free end of the thread is attached to the wall as shown in figure-5.74. Calculate the acceleration of the centre of mass of the spool , if its moment of inertia about its axis is Iand the radius of the wound thread layer is r.
⎡⎢⎣g sinθ1+Imr2⎤⎥⎦
 View Solution
View Solution

