The middle of a uniform rod of mass m and length l is rigidly fixed to a vertical axis OO′ so that the angle between the rod and the axis is equal to θ (figure). The ends of the axis OO′ are provided with bearings. The system rotates without friction with an angular velocity ω. Find:
(a) the magnitude and direction of the rod's angular momentum M relative to the point C, as well as its angular momentum relative to the rotation axis,
(b) how much the modulus of the vector M relative to the point C increases during a half-turn,
(c) the moment of external forces N acting on the axle OO′ in the process of rotation.
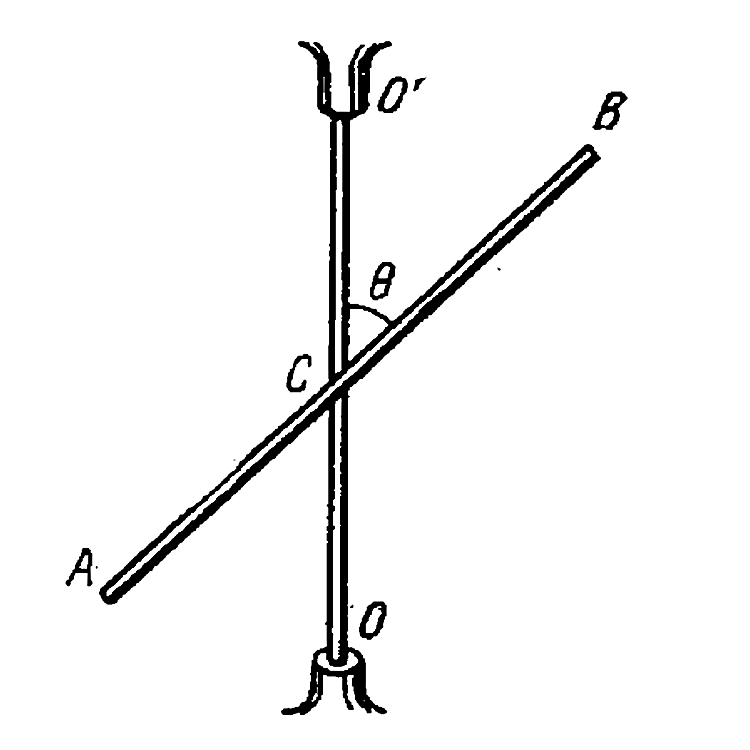
(a) The angular velocity ω about OO′ can be resolved into a component parallel to the rod and a component ωsinθ perpendicular to the rod through C. The component parallel to the rod does not contribute so the angular momentum
M=lωsinθ=112ml2ωsinθ
Also, Mz=Msinθ=112ml2ωsin2θ
This can be obtained directly also,
(b) The modulus of →M does not change but the modulus of the change of →M is ∣∣Δ→M∣∣.
∣∣Δ→M∣∣=2Msin(90−θ)=112ml2ωsin2θ
(c) Here M⊥=Mcosθ=Iωsinθcosθ
Now ∣∣∣d→Mdt∣∣∣=Iωsinθcosθωdtdt=124ml2ω2sin2θ
as →M precesses with angular velocity ω.

Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Elastic Deformation Of Asolid Body
25 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Hydrodynamics
25 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Universal Gravitation
34 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena
38 Videos
Similar Questions
Knowledge Check
A rod is rotating with angular velocity ω about axis AB. Find cosθ.
 Ag2lω2Bglω2C2g(lω)2D3g2lω2
Ag2lω2Bglω2C2g(lω)2D3g2lω2
A uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle θ with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed V in the horizontal plane then the angular momentum of the rod about the axis is:A12mVLcosθB13mVLsinθCmVLsincosθDzeroA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A12mω2xB12mω2(1−x2l)C12mω2l(1−x2l2)D12mω2l[1−xl]

A uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle θ with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed V in the horizontal plane then the angular momentum of the rod about the axis is:
View Solution
A uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle θ with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed V in the horizontal plane then the angular momentum of the rod about the axis is:
View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View Solution
A rod of mass 2 kg ad length 2 m is rotating about its one end O with an angular velocity ω=4rad/s. Find angular momentum of the rod about the axis rotation.
View Solution
A rod of mass 2 kg ad length 2 m is rotating about its one end O wth an angular velocity ω=4rad/s. Find angular momentum of the rod about the axis rotation.
View Solution

