A gyroscope, a uniform disc of radius R=5.0cm at the end of a rod of length l=10cm (figure), is mounted on the floor of an elevator car going up with a constant acceleration w=2.0m/s2. The other end of the rod is hinged at the point O. The gyroscope precesses with an angular velocity n=0.5rps. Neglecting the friction and the mass of the rod, find the proper angular velocity of the disc.
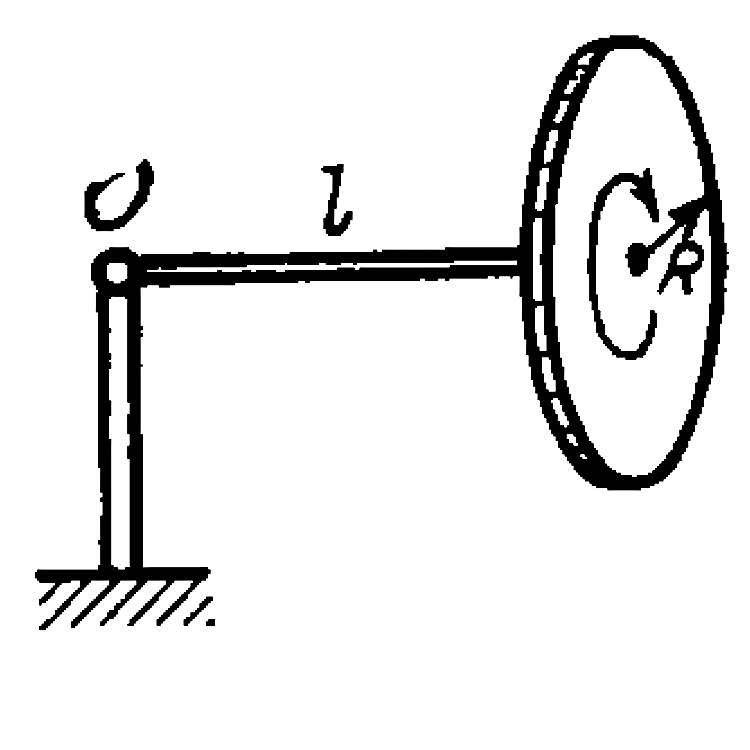
The moment of inertia of the disc about its symmetry axis is 1mR2. If the angular velocity of the disc is ω then the angular momentum is 12mR2ω. The precession frequency being 2πn,
we have ∣∣∣d→Mdt∣∣∣=12mR2ω×2πn
This must equal m(g+w)l, the effective gravitational torques (g being replaced by g+w in the elevator). Thus,
ω=(g+w)lπR2n=300rad/s
Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Elastic Deformation Of Asolid Body
25 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Hydrodynamics
25 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Universal Gravitation
34 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena
38 Videos
Similar Questions
A uniform rod of length l is spinning with an angular velocity ω=2vl while its centre of mass moves with a velocity v. Find the velocity of the end of the rod.

View SolutionA uniform rod of length l is spinning with an angular velocity ω=2vl while its centre of mass moves with a velocity v. Find the velocity of the end of the rod.

View Solution
Knowledge Check
In the figure shown the end A of the rod of length L is being pushed down parallel to the inclined surface with a velocity =v let the velocity of end B=u and the angular velocity of the rod = ω then
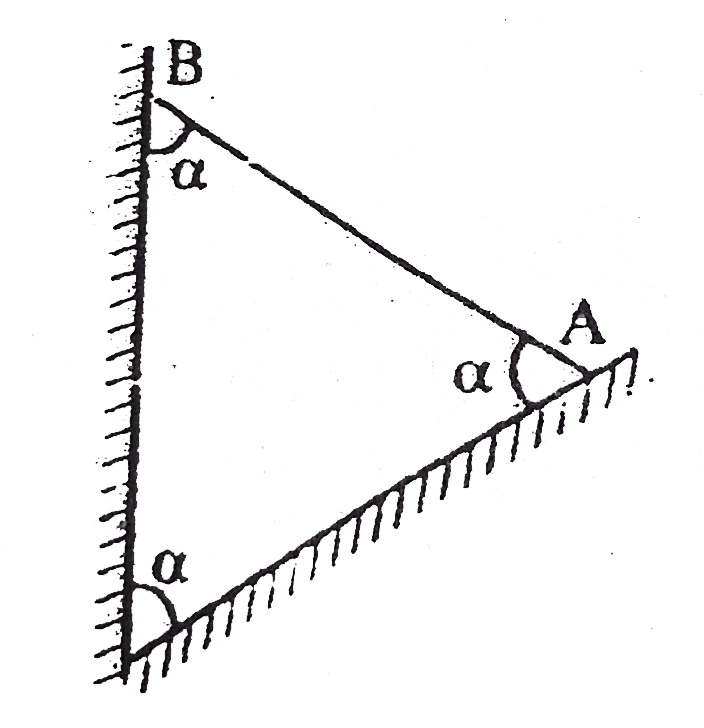 Au=vcosα (upward)Bu=v (downwards)Cω=vsinα/LDω=2vsinα/L
Au=vcosα (upward)Bu=v (downwards)Cω=vsinα/LDω=2vsinα/LA uniform rod AB of length l rotating with an angular velocity ω while its centre moves with a linear velocity v=ωl6 If the end A of the rod is suddenly fixed, the angular velocity of
 A34ωBω3Cω2D23ω
A34ωBω3Cω2D23ωIn the figure shown, the instantaneous speed of end A of the rod is v to the left. The angular velocity of the rod of length L must be
 Av2LBvLCv√32LDnone of these
Av2LBvLCv√32LDnone of these
In the figure shown, the instantaneous speed of end A of the rod is v to the left. The angular velocity of the rod of length L must be

View Solution
A rod of mass 2 kg ad length 2 m is rotating about its one end O with an angular velocity ω=4rad/s. Find angular momentum of the rod about the axis rotation.
View SolutionA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What is the rate of change of angular momentum of the rod ?

View SolutionA rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a masseless string tied to point Q as shown in Fig. When string is cut, the initial angular acceleration of the rod is :

View SolutionA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What is the rate of change of angular momentum of the rod ?

View Solution
