Two particles moving in a laboratory frame of reference along the same straight line with the same velocity v=(3/4)c strike against a stationary target with the time interval Δt=50ns. Find the proper distance between the particles prior to their hitting the target.
In the frame K in which the particles are at rest, their positions are A and B whose coordinates may be taken as,
A:(0,0,0),B=(l0,0,0)
In the frame K′ with respect to which K is moving with a velocity v the coordinates of A and B at time t′ in the moving frame are
A=(vt′,0,0)B=(l0√1−β2+vt′,0,0),β=vc
Suppose B hits a stationary target in K′ after time t′B while A hits it after time tB+Δt. Then,
l0√1−β2+vt′B=v(t′B+Δt)
So, l0vΔt√1−v2/c2

Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Hydrodynamics
25 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena
38 Videos
Similar Questions
Two particles start moving from the same point along the same straight line. The first moves with constant velocity v and the second with constant acceleration a. During the time that elapses before the sound catches the first, the greatest distance between the particle is.
View SolutionTwo relativistic particles move at right angles to each other in a laboratory frame of reference, one with the velocity v1 and the other with the velocity v2. Find their relative velocity.
View Solution
Knowledge Check
Two particles start moving from the same point along the same straight line. The first moves with constant velocity v and the second with constant acceleration a. During the time that elapses before the sound catches the first, the greatest distance between the particle is.
Av2aBv22aC2v2aDv24aTwo particles start moving from the same point along the same straight line. The first moves with constant velocity v and the second with constant acceleration a. During the time that elapses before the sound catches the first, the greatest distance between the particle is.
Av2aBv22aC2v2aDv24aTwo particles are moving along a straight line as shown. The velocity of approach between A and B is
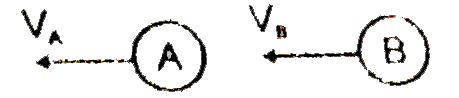 AVA+VBB|VA−VB|CVA−VBDVB−VA
AVA+VBB|VA−VB|CVA−VBDVB−VA
A particle move with a velocity v=αt3 along a straight line.The average velocity in time interval t=0 to t=T is
View SolutionTwo particles P and Q describe S.H.M. of same amplitude a, same frequency f along the same straight line from the same mean position. The maximum distance between the two particles is a √2, If the initial phase difference between the particles is πN then find N :
View SolutionTwo unstable particles move in the reference frame K along a straight line in the same direction with a velocity v=0.990c. The distance between them in this reference frame is equal to l=120m. At a certain moment both particles decay simultaneously in the reference frame fixed to them. What time interval between the moments of decay of the two particles will be observed in the frame K? Which particle decays later in the frame K?
View SolutionTwo particles are moving along a straight line as shown. The velocity of approach between A and B is
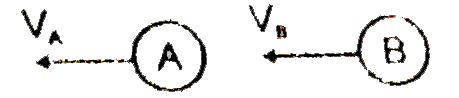
View SolutionTwo particles, A and B, move along the same straight line. At t=0, there velocities are zero. Look at their acceleration-time graphs and say whether the statements given below are true or false
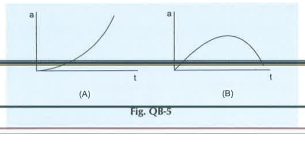
Both particles are moving in the same direction .
View Solution
