Fig, shows a toridal solenoidi whose cross-section is rectangular. Find the magnetic flux thorugh the winding equlals I=1.7A, the total number of turns Is N=1000, the ratio of the outside diameter to the inside one is η=1.6, and the height is equal to h=5.0cm.
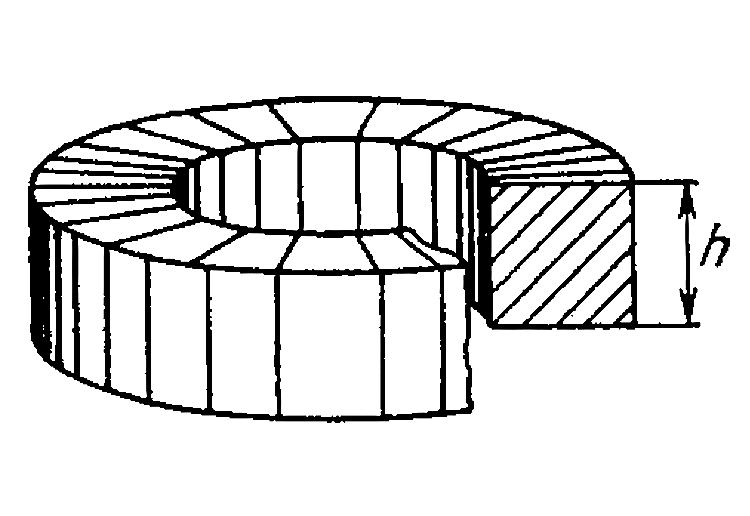
Bφ2πr=μ0NI
or, Bφ=μ0NI2πr
Then, Φ=∫baBφhdr,a≤r≤b=μ04π2Nlnη where η=b/a
Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electromagnetic Induction
84 Videos
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Motion Of Charged Particle In Magnetic Field
36 Videos
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Current
72 Videos
- ELECTRICITY AND MAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions
6 Videos
- ELECTROMAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions
24 Videos
Similar Questions
Figure-4.78 shows a toroidal solenoid whose cross-section is rectangular in shape. Find the magnetic flux through this cross-section if the current through the toroidal winding is I, total number of turns in winding is N, the inside and outside radii of the toroid are a and b respectively and the height of toroid is equal to h.

View SolutionA solenoid of length 2m and of radius 1 cm has a winding carrying a current of 0.1 ampere per turn. Find the magnetic field strength inside the solenoid if the total number of turns is 2000.
View Solution
Knowledge Check
A rectangular toroid has 1000 turns. The ratio of the outer to inner diameter is 1.6 and its height is 5.0 cm. Find the flux through this toroid, if current passing through it is 1.7 A.
A8μWbB6μWbC8WbD6WbA small coil is introduced between the poles of an electromagnet so that its axis coincides with the magnetic field direction. The cross-sectional area of the coil is equal to S=3.0mm2, the number of turns is N=60. When the coil turns through 180∘ about its diameter, a galvanometer connected to the coil indicates a charge q=4.5μC flowing through it. Find the magnetic induction magnitude between the poles, provided the total resistance of the electric circuit equals R=40Ω.
A2.5TB1.5TC0.5TD5T
An iron core shaped as a tore number of turns mean R=250mm. The supports a winding with the total number of turns N=1000. The core has a cross-cut of width b=1.00mm. With a current I=0.85 A flowing through the winding, the magnetic induction in the gap is equal to B=0.75T. Assuming the scarttering of the magnetic flux at the grap edges to be negligible, find the permeaiility of iron under these conditions.
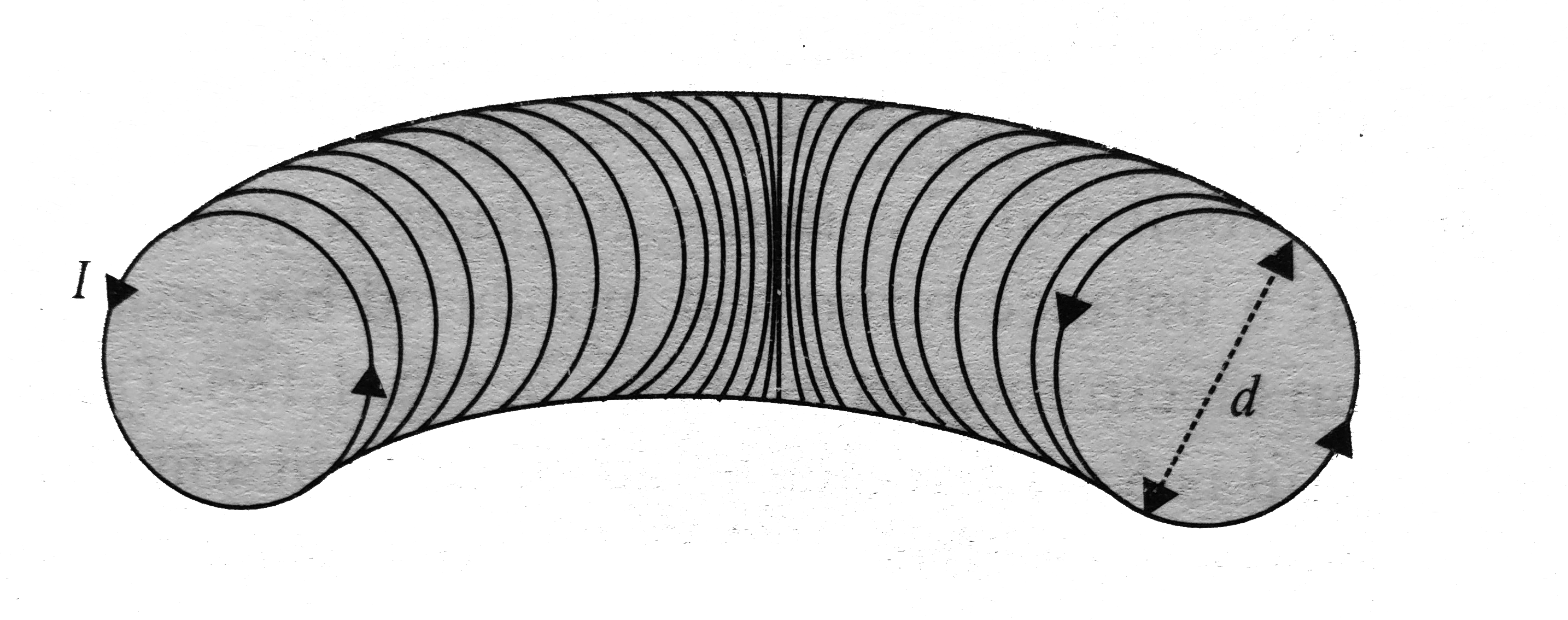
View SolutionCalculating the magnetic moment ( in Am2) of a thin wire with a current I=8A, wound tightly on a half a tore (see figure). The diameter of the cross section of the tore is equal to d=5cm, and the number of turns is N=500.
View SolutionFind the magnetic induction at the centre of a rectangular frame of wire whose diagonal is equal to d=16 cm and the angle between the diagonals is equal to ϕ=30∘, the current flowing in the frame equal to I=5.0A.

View SolutionA very long straight solenoid has a cross section radis R and n turns per unit lenghth. A direct current Iflows throguh the solenoid. Suppose that x is the distance from the end of the the solenoid, measured along its axis. Find:
(a) the magnetic induction B on the axis as a funciton of x, draw an approximate plot of B vs ratio x/R,
(b) the distance x0 to the point on the axis at which the value of B differs by η=1% from that in the middle section of the solnoid.
View Solution(a) Find magnetic field inside a long solenoid, carrying current (1/π) A and having number of turns per unit length 10. Also calculate magnetic field at ends.
(b) A long solenoid is fabricated by closely winding a wire of diameter 10mm over a cylinderical non-magnetic frame so that the successive turns nearly touch each other. Find magnetic field at the centre and ends of solenoid if it carriers a current (4/π) A?
(c) A single-layer coil (solenoid) has length l and cross-section radius R. The number of turns per unit length is equal to n. Find the magnetic induction at the centre of the coil when a current i flows through it.
(d) A solenoid of length 0.4m and diameter 0.6m consists of a single layer of 1000 turns of the fine wire carrying a current of 5mA. Calculate the magnetic field on the axis at the middle and at the ends of the solenoid.
View SolutionA thin wire is wound very tightly in one layer on the surface of a sphere of paramagnetic material (μr≈1). The planes of all the turns can be assumed to be perpendicular to the same diameter of the sphere. The turns over the entire surface of the sphere. The radius of the sphere is R, the total number of turns is N, and the current in the winding is I. Find the magnetic induction at the centre of the sphere. (Given μ0NI=20R)
View Solution
