Find the period of small oscillations in a vertical plane performed by a ball of mass fixed at the middle of a horizontallly stretched string in length. The tension of the string is assumed to be constant and equal to .
Let us locate and depict the forces ating on the ball at the position when it is at a distance down form the undeformed position of the string.
At this position, the unbalanced downward force on the ball
By Newton's lay
( when is small)
Thus
putting we get
Thus .

Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electric Oscillations56videos
OSCILLATIONS AND WAVES
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Elastic Waves39videos
OSCILLATIONS AND WAVES
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise2videos
OPTICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics49videos
PHYSICAL FUNDAMENTALS OF MECHANICS
Similar Questions
Find the period of small osciallations in a vertical plane performed by a small ball of mass m=50g fixed at the middle of a thin horizontal string of length l=1m and tensioned with a constant force T = 100N
View SolutionA 1m long rope, having a mass of 40g, is fixed at one end and is tied to a light string at the other end. The tension in the string in 400N. Find the wavelength in second overtone (in cm).
View Solution
Knowledge Check
- Question 1 - Select One
A partical of mass m is attached to a massless string of length l and is oscillating in a vrtical plane with the other end of the string fixed to a rigid support. The tension in the string at a certain instant is T=kmg .
Ak can never be geaater than 1Bk can never be less than 1Ck can never be equal than 1Dk can never be geaater than 3 - Question 2 - Select One
In the figure a rope of mass m and length l is such that its one end is fixed to rigid wall and the other is applied with a horizontal force F as shown below, then tension at the middle of the string is:
 AFB2FCZeroDF/2
AFB2FCZeroDF/2 - Question 3 - Select One
A stone of mass m is tied to a string and is moved in a vertical circle of radius r making n revolution per minute. The total tension in the string when the stone is its lowest point is.
Am[g+4π2r]Bm[g+π2n2r260]Cm[g+π2n2r900]Dm[g+n2r2]
A block of mass 1kg is tied to a string of length 1m the other end of which is fixed The block is moved on a smooth horizontal table with constant speed 10ms−1. Find the tension in the string
View SolutionA square plate of mass M and side length L is hinged at one of its vertex (A) and is free to rotate about it. Find the time period of small oscillations if
(a) the plate performs oscillations in the vertical plane of the figure. (Axis is perpendicular to figure.)
(b) the plate performs oscillations about a horizontal axis passing through A lying in the plane of the figure.
 View Solution
View SolutionFind the tension in the horizontal string PQ and the string QR in the given figure. [Take g=10m/s2]
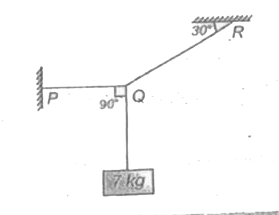 View Solution
View SolutionA string of 7m length has a mass of 0.035kg. If tension in the string is 60.N, then speed of a wave on the string is
View SolutionIn fig, all the pulleys and strings are massless and all the surfaces are frictionless. A small block of mass m is placed on fixed wedge (take f=10ms−2).

The tension in the string attached to m isView Solution

