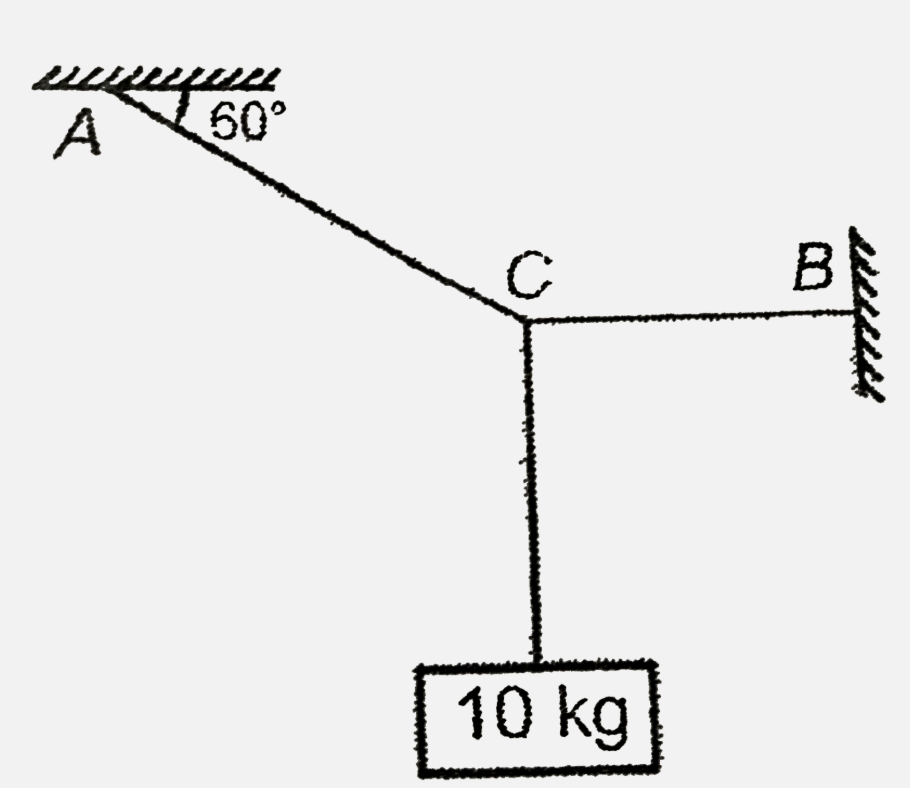
Find the tension in the horizontal string PQ and the string QR in the given figure. [Take g=10m/s2]
![Find the tension in the horizontal string PQ and the string QR in the given figure. [Take g=10m//s^(2)]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/AAK_P2_NEET_PHY_SP2_C05_SLV_015_Q01.png)
We may take the components and redraw it as
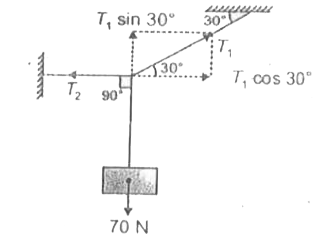
From figure, we get
T1sin30∘=70N
∴ By Lami's theorem, T1sin90∘=T2sin120∘=Wsin150∘
and T2=T1cos30∘
∴T1=140N
and T2=140×√32=70√3N
Alternate method:
As →T1+→T2+→W=→0
∴ By Lami's theorem T1sin90∘=T2sin120∘=Wsin150∘
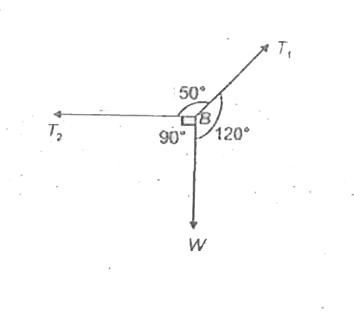
⇒T1=Wsin90∘sin150∘=2W=2×7×10=140N
and T2=Wsin120∘sin150∘=W×√3212=10×7×√3=70√3N
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE70videos
LAWS OF MOTION
- BOOK - AAKASH INSTITUTECHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-A)65videos
LAWS OF MOTION
- BOOK - AAKASH INSTITUTECHAPTER - LAWS OF MOTIONEXERCISE - ASSIGNMENT ( SECTION -J ) Aakash Challengers Questions5videos
LAWS OF MOTION
- BOOK - AAKASH INSTITUTECHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions10videos
KINETIC THEORY
- BOOK - AAKASH INSTITUTECHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)26videos
MAGNETISM AND MATTER
Similar Questions
Knowledge Check
- Question 1 - Select One
A body of mass 100 gram is tied at the end of a string of length 1m. It is rotated in a vertical circle at a critical speed of 4 m/s at the highest point . The tension in the string at the huighest point in its path is [ take g=10m/s2]
A0.3NB0.6NC0.9ND1.2N - Question 2 - Select One
Calculate the tension in the string shown in the figure. All the surfaces are frictionless. (Take g=10/ms−1)
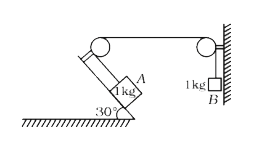 A2.5 NB5 NC7.5 ND10 N
A2.5 NB5 NC7.5 ND10 N
A block of mass 1 kg and density 0.8g/cm3 is held stationary with the help of a string as shown in figure. The tank is accelerating vertically upwards with an acceleration a =1.0m/s2. Find

(a) the tension in the string,
(b) if the string is now cut find the acceleration of block.
(Take g=10m/s2 and density of water =103kg/m3).View SolutionFind tension /tensions in the string/strings in the following cases:
 View Solution
View SolutionA uniform rod of length 1m and mass 2kg is suspended. Calculate tension T (in N) in the string at the instant when the right string snaps (g=10m/s2).
 View Solution
View SolutionA 2 kg block A is attached to one end of a light string that passes over an an ideal pulley and a 1 kg sleeve B slides down the other part of the string with an acceleration of 5m/s2 with respect to the string. Find the acceleration of the block, acceleration of sleeve and tension in the steing. [g=10m/s2]
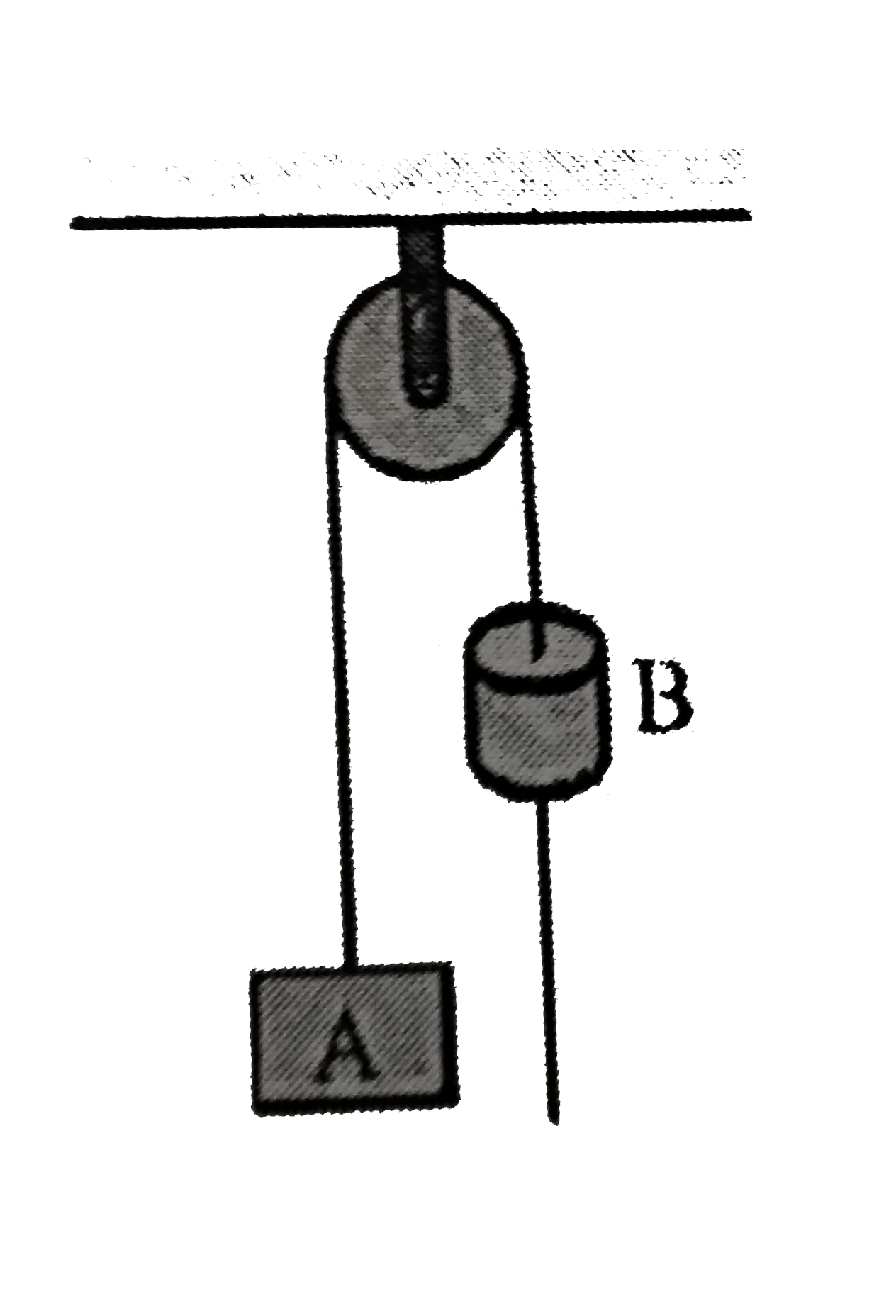 View Solution
View SolutionA 100 cm long wire of mass 40 g supports a mass of 1.6 kg as shown in figure . Find the fundamental frequency of the portion of the string between the wall and the pulley. Take g=10m/s2.
 View Solution
View SolutionTwo blocks with masses m1=0.2 kg and m2=0.3 kg hang one under other as shown in figure. Find the tensions in the strings (massless) in the following situations :
(g=10m/s2)
if maximum allowable tension is 10 N. What is maximum possible upward acceleration ?View Solution