A plane light wave wityh wavelength 0.60μm falls normally on a long opaque strip 0.70mm wide. Behind it a screen is placed at a distance 100cm. Using Fig. find the ratio of intensities of light in the middle of the diffraction pattern and at the edge of the geometrical shadow.
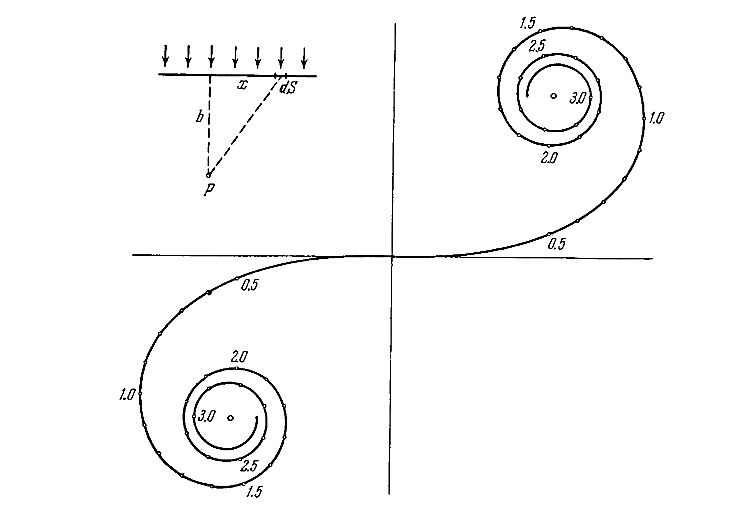
We shall use the equation written down in 5.103, the Fresnel-Huyghens formula.

Suppose we want to find the intensity at P which is such that the corrdinates of the edges (x-coordinates) with respect to P are x2 and −x1. Then, the amplitude at P is
E=∫K(φ)a0re−ikrdS
We write dS=dxdy,y is to integrated from −∞+0+∞. We write
r=b+x2+y22b.......(1)
(r is the disatnce of the element of surface on I from P. It is √b2+x2+y2 and hence appoximately (1)). Wer then get
E=A0(b)[∫∞0e−ikx2/2bdx+∫−x1−∞e−ikx2/2bdx]
=A'0(b)[∫∞v2e−iπu22du+∫−v1−∞e−iπu2/2du]
where v2=√2bλx2,v1√2bλx1
The intensity is the square of the amplitude. In our case, at the centre
v1=v2=√2bλ.a2=√a22bλ=0.64
(a= width of the strip =0.7mm,b=100cm,λ=0.60μm)
At, say, the lower edge v1=0,v2=1.28
Thus IcentreIedge=∣∣
∣∣∫∞0.64e−iπu2/2du+∫0.64−∞e−iπu2/2du∫∞1.28e−iπu2/2du+∫0−∞e−iπu2/2du∣∣
∣∣2=4(12−C(0.74))2+(12−S(0.64))21−C(1.28)2+(1−S(1.28))2
where C(v)=∫v0cos.πu22du
S(v)=∫v0sin.πu22du
Rough evaluation of the intergrals using corn's spiral gives
IcentreIedge≈2.4
(We have used ∫∞0cos.πu22du=∫∞0sin.πu22du=12
C(0.64)=0.62,S(0.64)=0.15
C(1.28)=0.65S(1.28)=0.67
Topper's Solved these Questions
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Polarization Of Light
43 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Dispersion And Absorption Of Light
24 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Interference Of Light
33 Videos
- MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - MECHANICSEXERCISE - Mechanics Problems
92 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
Similar Questions
A palne monochromatic ligth wave falls normally on a long rectangular slit behind which a screen is positioned at a distance b=60cm. First the width of the slit has adjucted so that in the middle of the diffraction pattern the lowest minimum was observed. After widening the slit by Δh0.70mm, the next minimum was obtained in the centre of the pattern. Find the wavelength of light.
View SolutionA plane light wave with wavelength λ=0.65μm falls normally on a large glass plate whose opposite side has a longrectangular recess 0.60mm wide. Using Fig. find the depth H of the recess at which the diffraction pattern on the screen 77cm away from the plate has the maximum illuminance at its centre.
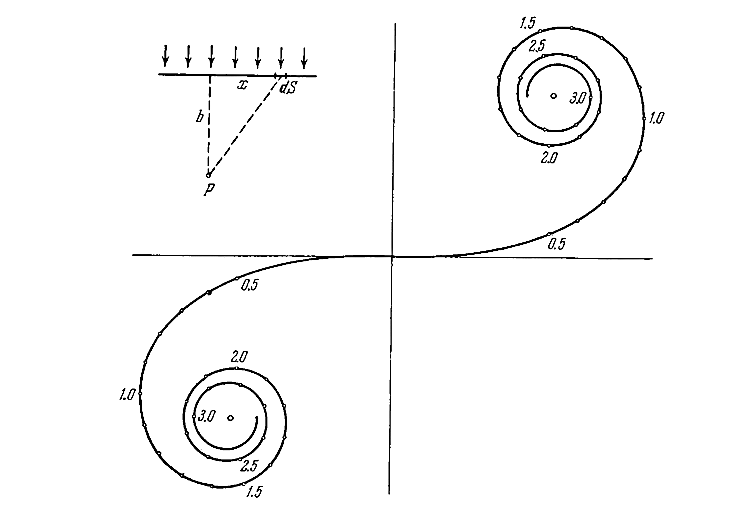
View Solution
Knowledge Check
Light of wavelength λ=5000Å falls normally on a narrow slit. A screen is placed at a distance of 1m from the slit and perpendicular to the direction of light. The first minima of the diffraction pattern is situated at 5mm from the centre of central maximum. The width of the slit is
A(a) 0.1mmB(b) 1.0mmC(c) 0.5mmD(d) 0.2mm
Light of wavelength λ=5000Å falls normally on a narrow slit. A screen is placed at a distance of 1m from the slit and perpendicular to the direction of light. The first minima of the diffraction pattern is situated at 5mm from the centre of central maximum. The width of the slit is
View SolutionA plane light wave with wavelength λ=0.65μm falls normally on a large glass plate whose opposite side has a large and an opaque strip of width a=0.30mm (Fig.) A screen is placed at a distance b=110cm from the plate. The height h of the ledge is such that the intensity of light at point 2 of the screen is the heighest possible. making use of Fig. find the ratio of intensities at point 1 and 2.
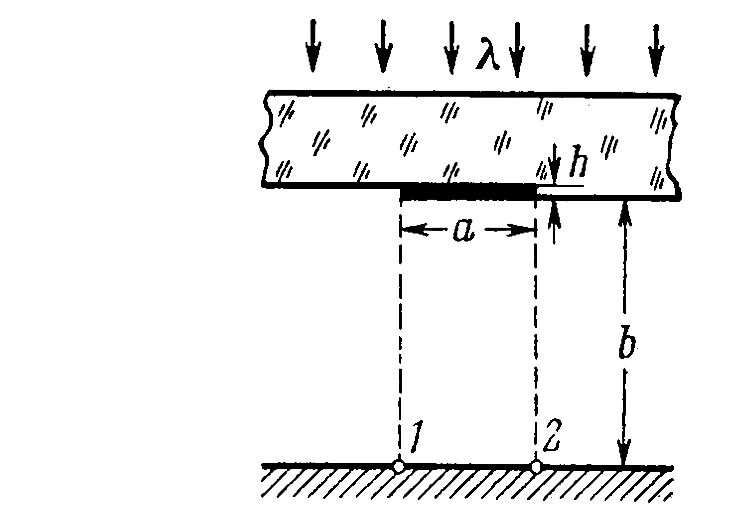
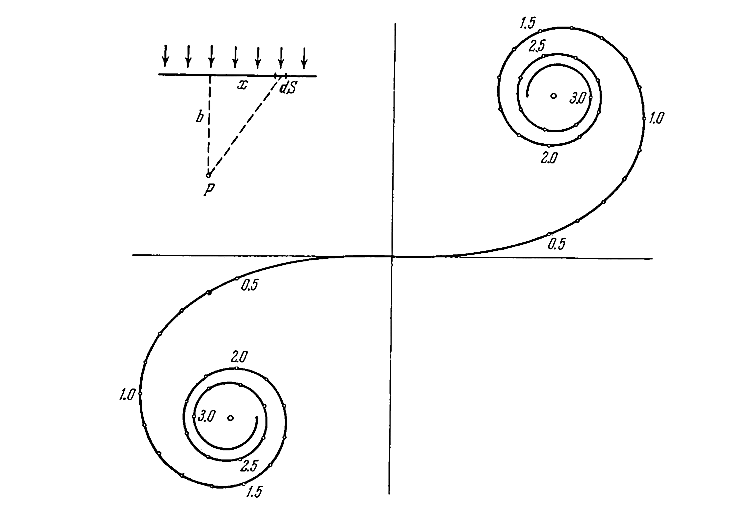
View SolutionA plane monochromatic light wave falls normally on an opaque screen with a long slit whose shape is shown in Fig. Making use of Fig. find the ratio of intensities of light at points 1,2 and 3 located behind the screen at equal distances from it. For point 3 the rounded-off edge of the slit coincides with the boundary line of the first Fresnel zone.
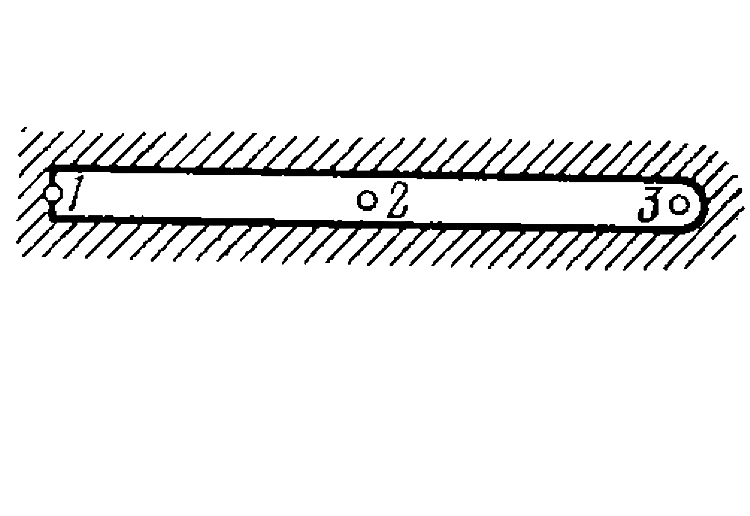
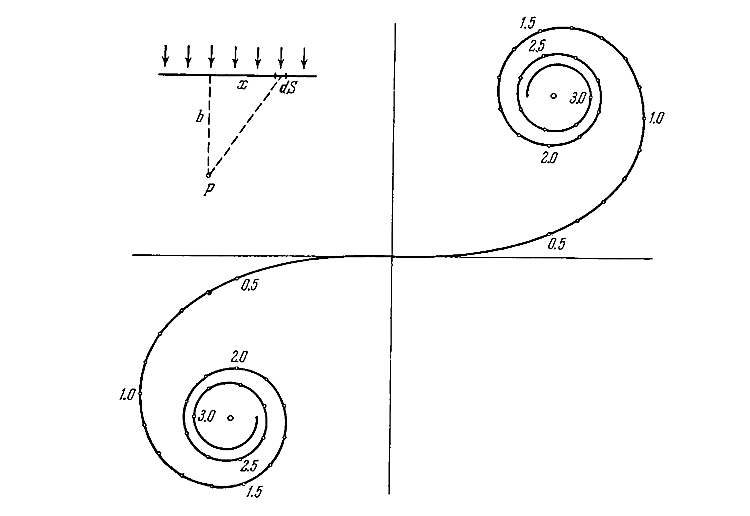
View SolutionA plane monochromatic light wave falls normally on an opaque half-plane. A screen is located at a distance b=100cm behind the half-plane. Making use of the cornu spiral (Fig.) find :
(a) the ratio of intensities of the first maximum and the neighbouring minimum,
(b) the wavelength of light if the first two maxima are separated by a distance Δx=0.63mm.
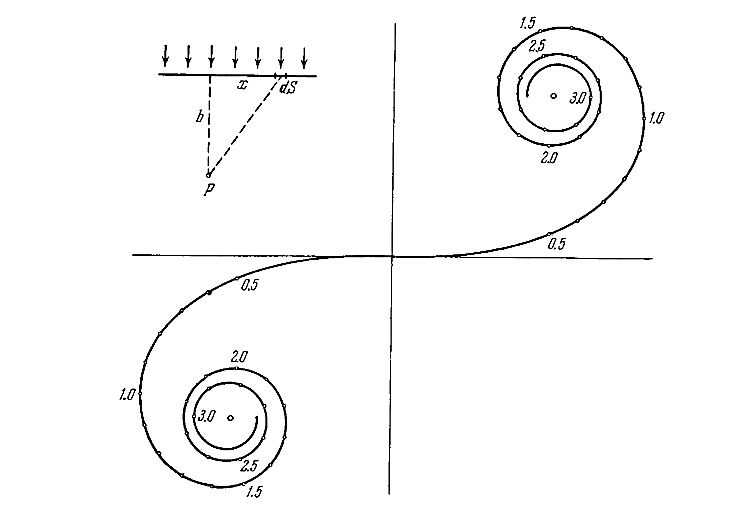
View SolutionLight of wavelength 600 nm falls from a distant source on a slit 0.6 mm wide. Find the distance between the two dark bands, on either side of the central bright band of the diffraction pattern observed , on a screen placed 2 m from the slit.
View SolutionA plane monochromatic light wave with intensity I0 falls normally on the surfaces of the opaque screens shown in Fig. Find the intensity of light I at a point P

(a) located behind the corner ponts of screens 1−3 and behind the edge of half-plane 4,
(b) for which the rounded-off edge of screens 5−8 coincides with the boundary of the first formula describing the result obtained for screens 1−4, the same, for screens 5−8.
View SolutionA plane monochromatic light wave with intensity I0 falls normally on an opaque screen with a round aperture. What is the intensity of light I behind the screen at the point for which the aperture
(a) is equal to the first Fresnel zone, to the internal half of the first zone,
(b) was made equal to the first Fresnel zone and then half of it was closed (along the diameter) ?
View Solution
