A plane light wave with wavelength λ=0.60μm falls normally on the face of a glass wedge with refracting angle Θ=15∘. The opposite face of the wedge is opaque and has a slit of width b=10μm parallel to the edge. Final:
(a) the angle Δθbetween the direction to the Fqaunhofer maximum of zeroth order and that of incident light,
(b) the angular width of the frqunhofer maximum of the zeroth order.
This case is analogous to the previous one except that the incident wave moves in glass of R.I.n. Thus the expression for the path difference for light diffracted at angle θ from the normal to the hypotenuse of the wedge is
b(sinθ−nsinΘ)
we write θ=Θ+Δθ
Then for the direction of principle Fraunhofer maximum
b(sin(Θ+Δθ)−nsinΘ)=0
or Δθ=sin−1(nsinΘ)−Θ
Using Θ=15∘,n=1.5 we get
Δθ=7.84∘
(b) The width of the central maximum is obtained from (λ=0.60μm,b=10μm)
b(sinθ1−nsinΘ)=±λ
Thus θ+1sin−1(nsinΘ+λb)=26.63∘
θ−1=sin−1(nsinΘλb)=19.16∘
∴δθ=θ+1−θ−1=7.47∘

Topper's Solved these Questions
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Polarization Of Light
43 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Dispersion And Absorption Of Light
24 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Interference Of Light
33 Videos
- MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - MECHANICSEXERCISE - Mechanics Problems
92 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
Similar Questions
A plane light wave with wavelength λ=0.50μm falls normally on the face of a glass wedge with an angle Θ=30∘. On the opposite face of the wedge a transparent diffraction grating with period, d=2.00μm is inscibed, whose lines are parallel to the wedge's edge. Find the angles that the direction of incident light froms with the directions to the principle Fraunhofer maxima of the zero and the first order. waht is the highest order of the spectrum? At what angle to the direction of incident light of the observed?
View SolutionA plane monochromatic light wave with wavelength λ falls on the surface of a glass wedge whose faces from an angle α<<1. The plane of incidence is perpendicualr to the edge, the angle of incidence is θ1. Find the distance between the neighbouring fringe maxima on the screen placed at right angles to reflected light.
View Solution
Knowledge Check
Light falls at normal incidence on one face of a glass prism of refractive index √2. Then the angle of emergence when the angle of the prism is 45∘
A45°B60°C15°D90°A beam of monochromatic light of wavelength λ falls normally on a diffraction grating of line spacing d. If θ is the angle between the second-order diffracted beam and the direction of the incident light, what is the value of sinθ ?
AλdBdλC2λdD2dλ
Find the minimum and maximum deflectrion angls for a light ray passing through a glass prism with refracting angle θ=60∘.
View SolutionLight with wavelength λ=0.50μm falls on a slit of width b=10μm at an angle θ0=30∘ to its normal. Find the angular position of the first minima located on both sides of the central Fraunhofer maximum.
View SolutionLight with wavelength λ=0.55μm from a distant point source falls normally on the surface of a glass wedge. A fringe pattern whose neighbouring maxima on the surface of the wedge are separated by a distance Δx=0.21mm is observed in reflected light. Find:
(a) the angle between the wedge faces,
(b) the degree of light monochromatism (Δλ/λ) if the fringes disappear at a distance l≈1.5cm from the wedge's edge.
View SolutionFind the wavelength of monochromatic light falling normally on a diffraction grating with period d=2.2μm if the angle between the directions to the Fraunhofer maxima of the first and the second order is equal to Δθ=15∘.
View SolutionA plane light wave with wavelength λ=0.65μm falls normally on a large glass plate whose opposite side has a large and an opaque strip of width a=0.30mm (Fig.) A screen is placed at a distance b=110cm from the plate. The height h of the ledge is such that the intensity of light at point 2 of the screen is the heighest possible. making use of Fig. find the ratio of intensities at point 1 and 2.
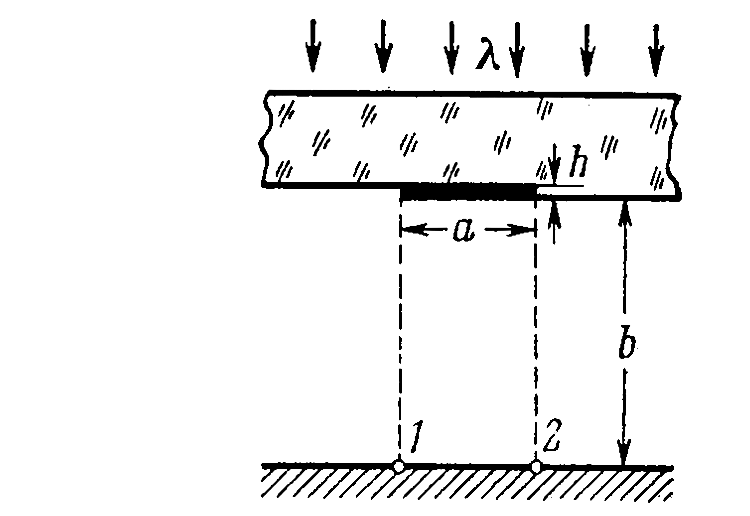
View SolutionA ray of light incident normally on the first face of a glass prism of refractive index 1.6 just emerges from the other face. Find the angle of the prism.
View Solution
