A uniform rope of length 12 mm and mass 6 kg hangs vertically from a rigid support. A block of mass 2 kg is attached to the free end of the rope. A transverse pulse of wavelength 0.06 m is produced at the lower end of the rope. What is the wavelength of the pulse when it reaches the top of the rope?
0.6 m
0.32 m
0.24 m
0.12 m
The correct Answer is:D
Tension at the lower end of the rope = 2 kg weight
Tension at the top of the rope =6+2=8kg weight ltrbgt 
∵v=√Tm∵vTopvLower=√TTopTLower=√82=2…(1)
As the frequency (n) remains constant, equation (1) will be
vTopvLower=nλTopnλLower=2 ∴λTop0.06=2
λTop=0.12m
Topper's Solved these Questions
- WAVE MOTIONBOOK - MARVEL PUBLICATIONCHAPTER - WAVE MOTIONEXERCISE - Test your grasp
15 Videos
- SURFACE TENSION BOOK - MARVEL PUBLICATIONCHAPTER - SURFACE TENSION EXERCISE - MULTIPLE CHOICE QUESTIONS . (TEST YOUR GRASP )
10 Videos
- WAVE THEORY OF LIGHT AND POLARISATION BOOK - MARVEL PUBLICATIONCHAPTER - WAVE THEORY OF LIGHT AND POLARISATION EXERCISE - TEST YOUR GRASP -10
15 Videos
Similar Questions
A uniform rope of length 12m and mass 6kg hangs vertically from a rigid support. A block of mass 2kg is attached to the free end of the rope. A transverse pulse of wavelength 0.06m is produced at the lower end of the rope. What is the wavelength of the pulse whwn it reaches the top of the rope?
View SolutionA uniform rope of length 10 cm and mass 4 kg hangs vertically from a rigid support. A block of mass 2 kg is attached to the free end of the rope. A transverse pulse of wavelength 0.06 m is produced at the lower end of the rope, what is the wavelength of the pulse when it reaches the top of the rope?
View Solution
Knowledge Check
A uniform rope of length 10 m and mass 3 kg hangs vertically from a rigid support. A block of mass 1 kg is attached to the free end of the rople. A transverse pulse of wavelength 0.05 m is produced at the lower end of the rope. The wavelength of the pulse when it reaches the top of the rope is
A0.10 mB0.12 mC0.16 mD0.18 mA uniform rope of legnth L and mass m1 hangs vertically from a rigid support. A block of mass m2 is attached to the free end of the rope. A transverse pulse of wavelength λ1 is produced at the lower end of the rope. The wavelength of the pulse when it reaches the top of the rope is λ2. The ratio λ2λ1 is
A√m1m2B√m1+m2m2C√m2m1D√m1+m2m1A uniform rope of legnth L and mass m1 hangs vertically from a rigid support. A block of mass m2 is attached to the free end of the rope. A transverse pulse of wavelength λ1 is produced at the lower end of the rope. The wavelength of the pulse when it reaches the top of the rope is λ2. The ratio λ2λ1 is
A√m1+m2m1B√m1m2C√m1+m2m2D√m2m1
A uniform rope of length 20m and mass 8kg hangs vertically froma rigid support. A block of mass 2kg is attached to the free end of the rope. A transverse pulse of wavelength 0.06m is produced at the lower end of the rope. What is the wavelength of the pulse when it reaches the top os the rope?
View SolutionA uniform rope of length 10 m and mass 15 kg hangs vertically from a rigid support. A block of mass 5 kg is attached to the free end of the rope. A transverse pulse of wavelength 0.08 m is produced at the lower end of the 3 rope. The wavelength of the pulse when it reaches the top of the rope will be-
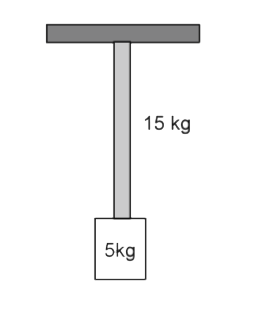
View SolutionA uniform rope of mass 6 kg and length 6 m hangs vertically from a rigid support. A block of mass 2 kg is attached to the free end of the rope. A transverse pulse of wavelength 0.075 m is produced at the lower end of the rope. The wavelength of the pulse when it reaches the top of the rope is K cm where K is
View SolutionA uniform rope of mass 6 kg and length 6 m hangs vertically from a rigid support. A block of mass 2 kg is attached to the free end of the rope. A transverse pulse of wavelength 0.075 m is produced at the lower end of the rope. The wavelength of the pulse when it reaches the top of the rope is K cm where K is
View SolutionA uniform rope of length L and mass m1 hangs vertically from a rigid support. A block of mass m2 is attached to the free end of the rope. A transverse pulse of wavelength λ1 is produced at the lower end of the rope. The wavelength of the pulse when it reaches the top of the rope is λ2. The ratio λ2λ1 is
View Solution
