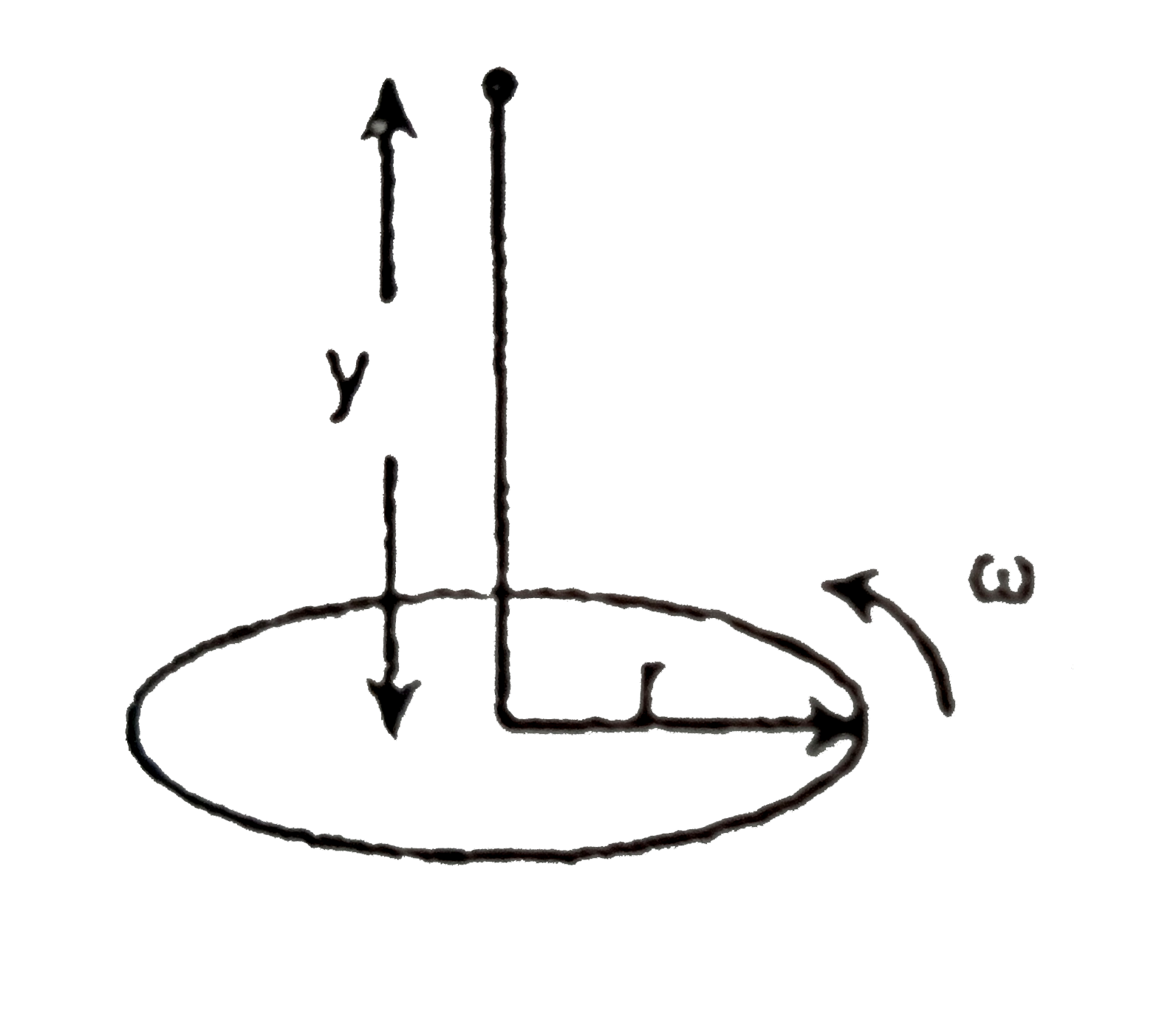
Calculate the magnetic field at distance from the centre of the axis of a disc of radius and unifrom surface charge density , If the disc spins with angular velocity ?
The correct Answer is:B
Step by step video & image solution for Calculate the magnetic field at distance y from the centre of the axis of a disc of radius r and unifrom surface charge density sigma, If the disc spins with angular velocity omega ? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MAGNETIC EFFECT OF ELECTRIC CURRENTBook:TARGET PUBLICATIONChapter:MAGNETIC EFFECT OF ELECTRIC CURRENTExercise:COMPETITIVE THINKING
Explore 111 Videos
- KINETIC THEORY OF GASES AND RADIATION Book:TARGET PUBLICATIONChapter:KINETIC THEORY OF GASES AND RADIATION Exercise:Evaluation test
Explore 18 Videos
- MAGNETISMBook:TARGET PUBLICATIONChapter:MAGNETISMExercise:EVALUATION TEST
Explore 14 Videos
Similar Questions
Knowledge Check
A charge q is placed at the some distance along the axis of a uniformly charged disc of surface charge density σ. The flux due to the charge q through the disc is ϕ. The electric force on charge q exerted by the disc is
AσϕBσϕ4πCσϕ2πDσϕ3π
Find the potential φ at the edge of a thin disc of radius R carrying the uniformly distributed charge with surface density σ.
View SolutionCalculate electric field at a point on axis, which at a distance x from centre of uniformly charged disc having surface charge density σ and R which also contains a concentric hole of radius r.
View SolutionA disc of radius R rotates at an angular velocity ω about the axis perpendicular to its surface and passing through its centre. If the disc has a uniform surface charge density σ, find the magnetic induction on the axis of rotation at a distance x from the centre. (Given R=3m, x=4m and μ0σω=20Tesla/m.)
View SolutionA thin copper ring of radius a is charged with q units of electricity. Calculate the electric field at a point at a distance x from the centre and on the axis of the ring. Use the result to find the electirc field due to a charged disc of surface density of charge ε.
View SolutionFind the electric field caused by a disc of radius a with a uniform surfce charge density σ (charge per unit area) at a point along the axis of the disc a distance x from its centre.
View SolutionThe diagram shows a part of disc of radius R carrying uniformly distributed charge of density σ. Electric potential at the centre O of parent disc is
View SolutionA man of mass m stands on a horizontal platform in the shape of a disc of mass m and radius R, pivoted on a vertical axis through its centre about which it can freely rotate. The man starts to move around the centre of the disc in a circle of radius r with a velocity v relative to the disc. Calculate the angular velocity of the disc.

View Solution
