A disc of radius R rotates at an angular velocity ω about the axis perpendicular to its surface and passing through its centre. If the disc has a uniform surface charge density σ, find the magnetic induction on the axis of rotation at a distance x from the centre. (Given R=3m, x=4m and μ0σω=20Tesla/m.)
Consider a ring of radius r and width dr.
dq=(2πrdr)σ
Current due to the ring is
dI=ωdq2π=σωrdr
Magnetic field due to this ring at point P is,
dB=μ0dIr22(r2+x2)3/2
or ∫dB=μ0σω2∫R0r3dr(r2+x2)3/2
Substituting r2+x2=t2, and 2rdr=2tdt and integrating we have
B−μ0σω2[R2+2x2√T2+x2−2x].

Topper's Solved these Questions
Similar Questions
A metal disc of radius R rotates with an angular velcoity ω about an axis perpendicular to its plane passing through its centre in a magnetic field B acting perpendicular to the plane of the disc. Calculate the induced emf between the rim and the axis of the disc.
View SolutionFind the moment of inertia of a uniform half-disc about an axis perpendicular to the plane and passing through its centre of mass. Mass of this disc is M and radius is R.
View Solution
Knowledge Check
Radius of gyration of disc rotating about an axis perpendicular to its plane passing through through its centre is (If R is the radius of disc)
AR2BR√2CR√3DR3A disc of radius R rotates with constant angular velocity ω about its own axis. Surface charge density of this disc varies as σ=αr2, where r is the distance from the centre of disc. Determine the magnetic field intensity at the centre of disc.
Aμ0αωR3Bμ0αωR36Cμ0αωR38Dμ0αωR33Calculate the magnetic field at distance y from the centre of the axis of a disc of radius r and unifrom surface charge density σ, If the disc spins with angular velocity ω ?
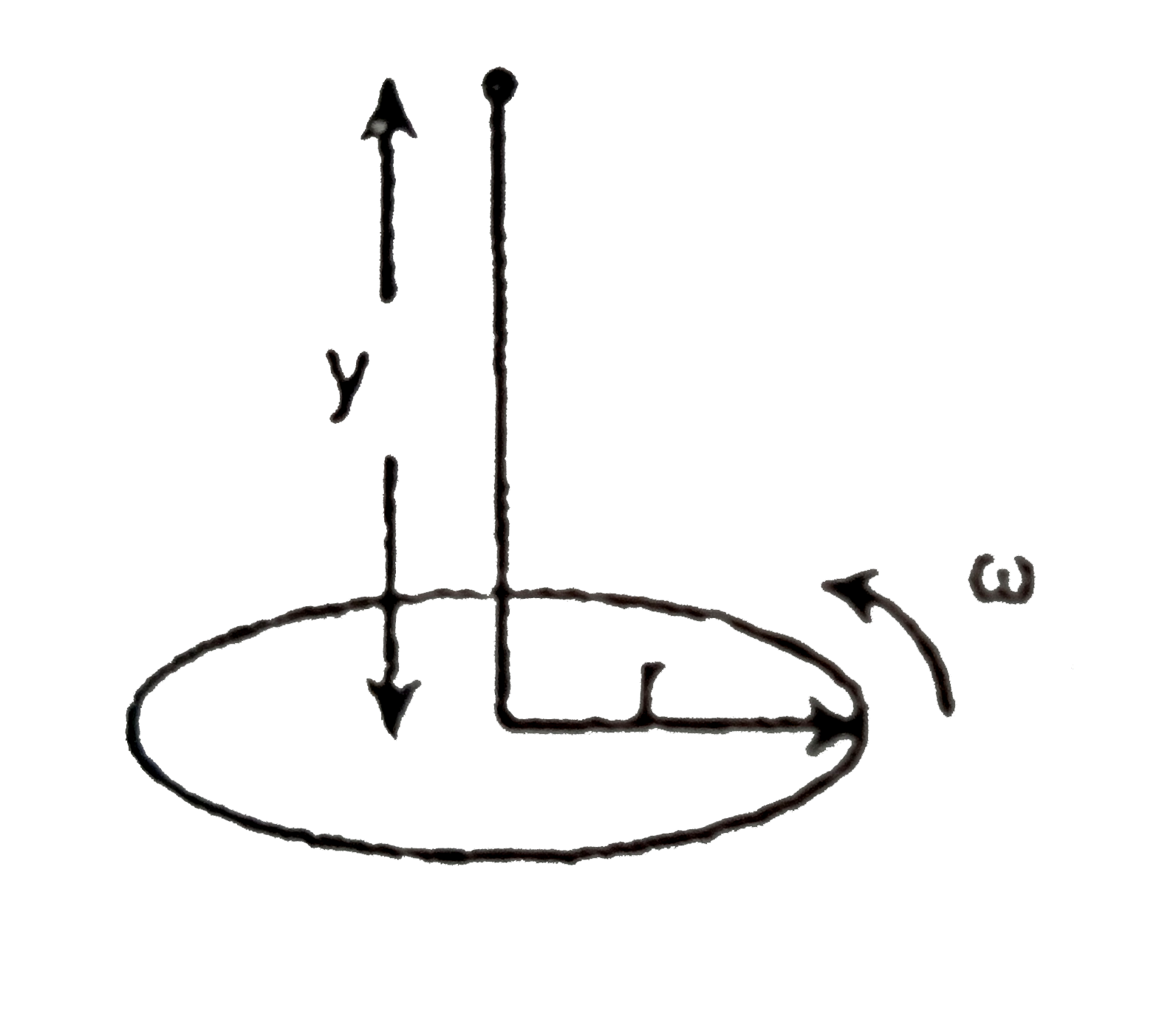 Aμ0σω3(r2−2y2√r2−y2+2y)Bμ0σω2(r2+2y2√r2+y2)Cμ0σω2(r2+2y2√r2+y2−2y)D2μ0σω3(r2+2y2√r2+y2−2y)
Aμ0σω3(r2−2y2√r2−y2+2y)Bμ0σω2(r2+2y2√r2+y2)Cμ0σω2(r2+2y2√r2+y2−2y)D2μ0σω3(r2+2y2√r2+y2−2y)
A disc of radius R rotates with constant angular velocity ω about its own axis. Surface charge density of this disc varies as σ=αr2, where r is the distance from the centre of disc. Determine the magnetic field intensity at the centre of disc.
View SolutionCalculate the magnetic field at distance y from the centre of the axis of a disc of radius r and unifrom surface charge density σ, If the disc spins with angular velocity ω ?

View SolutionA sphere of radius R, uniformly charged with the surface charge density σ rotates around the axis passing through its centre at an angular velocity. (a) Find the magnetic induction at the centre of the rotating sphere. (b) Also, find its magnetic moment.
View SolutionA non-conducting thin disc of radius R charged uniformly over one side with surface density σ, rotates about its axis with an angular velocity ω. Find (a) the magnetic field induction at the centre of the disc (b) the magnetic moment of the disc.
View SolutionOne quarter sector is cut from a uniform disc of radius R. This sector has mass M. It is made to rotate about a line perpendicular to its plane and passing through the centre of the original disc. What is its moment of inertia about the axis of rotation ?
View Solution
