Let C1 be the circle of radius 1 with center at the origin. Let C2 be the circle of radius r with center at the point A=(4,1), where 1<r<3. Two distinct common tangents PQandST of C1 and C2 are drawn. The tangent PQ touches C1 at P and C2 at Q. The tangent ST touches C1 at S and C2 at T. Mid points of the line segments PQandST are joined to form a line which meets the x -axis at a point B . If AB=√5 , then the value of r2 is
Step by step video solution for Let C_1 be the circle of radius 1 with center at the origin. Let C_2 be the circle of radius r with center at the point A = (4,1), where 1 lt r lt 3. Two distinct common tangents PQ and ST of C_1 and C_2 are drawn. The tangent PQ touches C_1 at P and C_2 at Q. The tangent ST touches C_1 at S and C_2 at T. Mid points of the line segments PQ and ST are joined to form a line which meets the x -axis at a point B . If AB = sqrt5 , then the value of r^2 is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Let C1 be the circle of radius r>0 with centre at (0,0) and let C2 be the circle of radius r with centre at (r,0) .The length of the arc of the circle C1 that lies inside the circle C2 ,is
View SolutionTwo circles of radius r1andr2 touches externally at point A have a common tangent PQ. Then find the value of PQ2.
View Solution
Knowledge Check
C1 is a circle with centre at the origin and radius equal to r and C2 is a circle with centre at (3r, 0) and radius t 2r. The number of common tangents that can be drawn to the two circles are
A1B2C3D4In the figure , PQ and PT are tangents. AB is a third tangent touching the circle at C. If PQ = 35 cm , then the perimeter of ΔPAB is
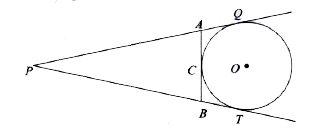 A70 cmB35√2 cmC35√3 cmD35 cm
A70 cmB35√2 cmC35√3 cmD35 cm
Let C be the circle of radius unity centred at the origin. If two positive numbers x1andx2 are such that the line passing through (x1,−1)and(x2,1) is tangent to C then x1⋅x2
View SolutionTwo circles of radius 1 and 4 touch each other externally. Another circle of radius r touches both circles externally and also one direct common tangent of the two circles. Then [1r]=
View SolutionTwo circles with radii a and b respectively touch each other externally . Let c be the radius of a circle that touches these two circles as well as a common tangent to the circles. Then
View SolutionLet C be the circle with centre at (1, 1) and radius = 1. If T is the circle centred at (0, y), passing through origin and touching the circle C externally, then the radius of T is equal to (1) √3√2 (2) √32 (3) 12 (3) 14
View SolutionThe internal common tangents to two circles with centre C1 and C2 intersect the line joining C1 andC2 at P and the two direct common tangents intersects the line joining C1 and C2 at Q. The length C1P, C1C2 are C1 Q are in
View SolutionThe circle C has its centre at (−1,1) and touches both the coordinate axes. From a point P(2,3) tangents are drawn to touch C at Q and R. The equation of the line joining the midpoints of PQ and PR is
View Solution
