Gravitational field intensity at the centre of the semi circle formed by a thin wire of mass and length is
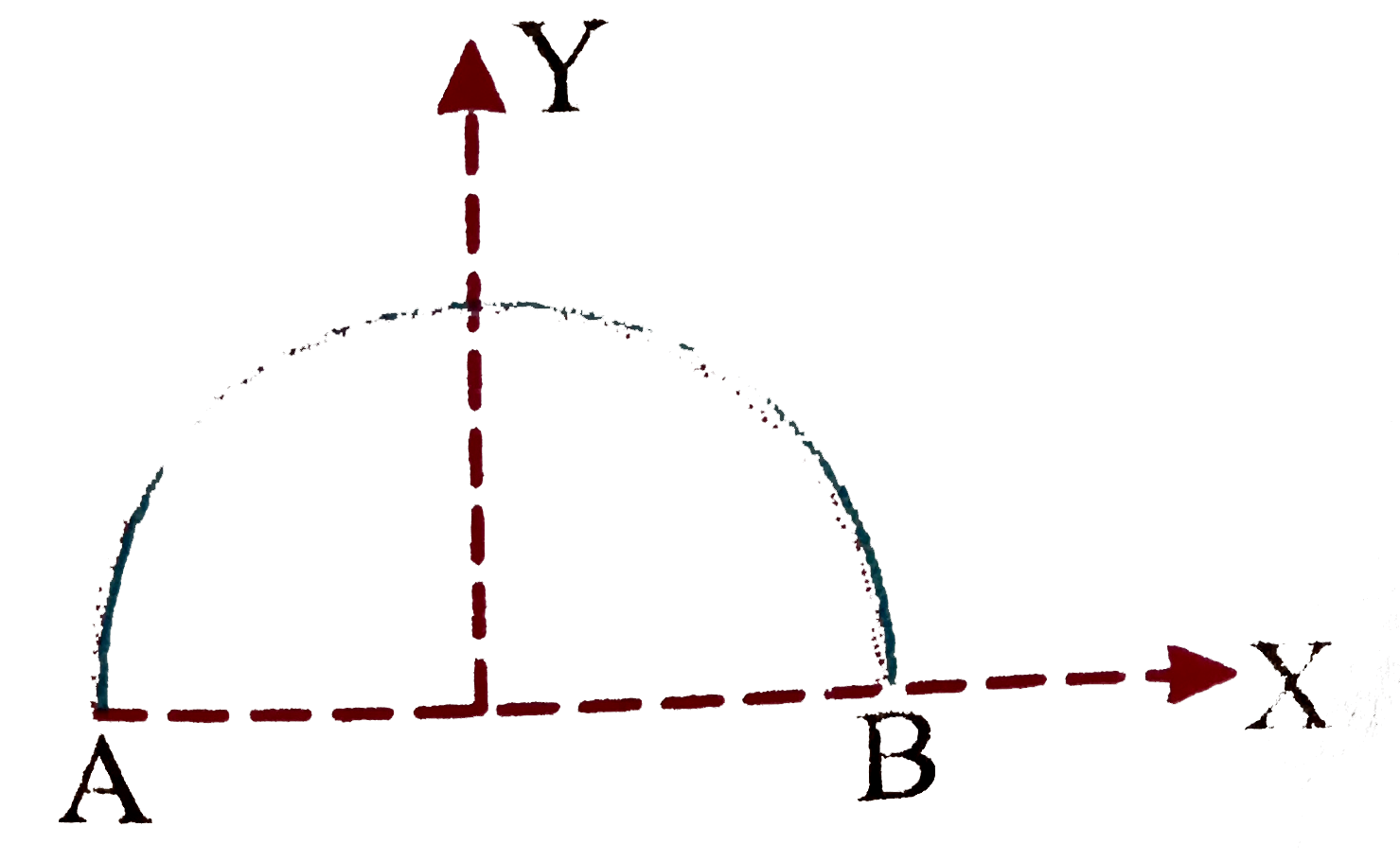
The correct Answer is:D
Topper's Solved these Questions
- GRAVITATIONBOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - NCERT BASED QUESTIONS
26 Videos
- GRAVITATIONBOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - LEVEL -I(H.W)
56 Videos
- GRAVITATIONBOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - LEVEL II (C.W.)
38 Videos
- FRICTIONBOOK - NARAYNACHAPTER - FRICTIONEXERCISE - Passage type of questions I
6 Videos
- KINETIC THEORY OF GASESBOOK - NARAYNACHAPTER - KINETIC THEORY OF GASESEXERCISE - LEVEL-III(C.W)
52 Videos
Similar Questions
Calculate the gravitational field intensity at the centre of the base of a hollow hemisphere of mass M and radius R. (Assume the base of hemisphere to be open)

View SolutionCalculate the gravitational field intensity and potential at the centre of the base of a solid hemisphere of mass m, radius R
View Solution
Knowledge Check
If gravitational field Intensity is E at distance R/2 outside from then surface of a thin shell of radius R , the gravitational field intensity at distance R/2 from its centre is
AZeroB2EC2E3D3E2Choose the most appropriate option.
The potential energy of gravitational interaction of a point mass m and a thin uniform rod of mass M and length L, if they are located along a straight line at a distance a from each other, isAU=GMmaln(a+Lα)BU=GMm(1a−1a+L)CU=−GMmaDU=−GMmLln(a+La)A uniform rod of mass m and length l is taken. Find the gravitational field intensity at point P at distance d which is on the perpendicular bisector of the rod as shown in Fig.
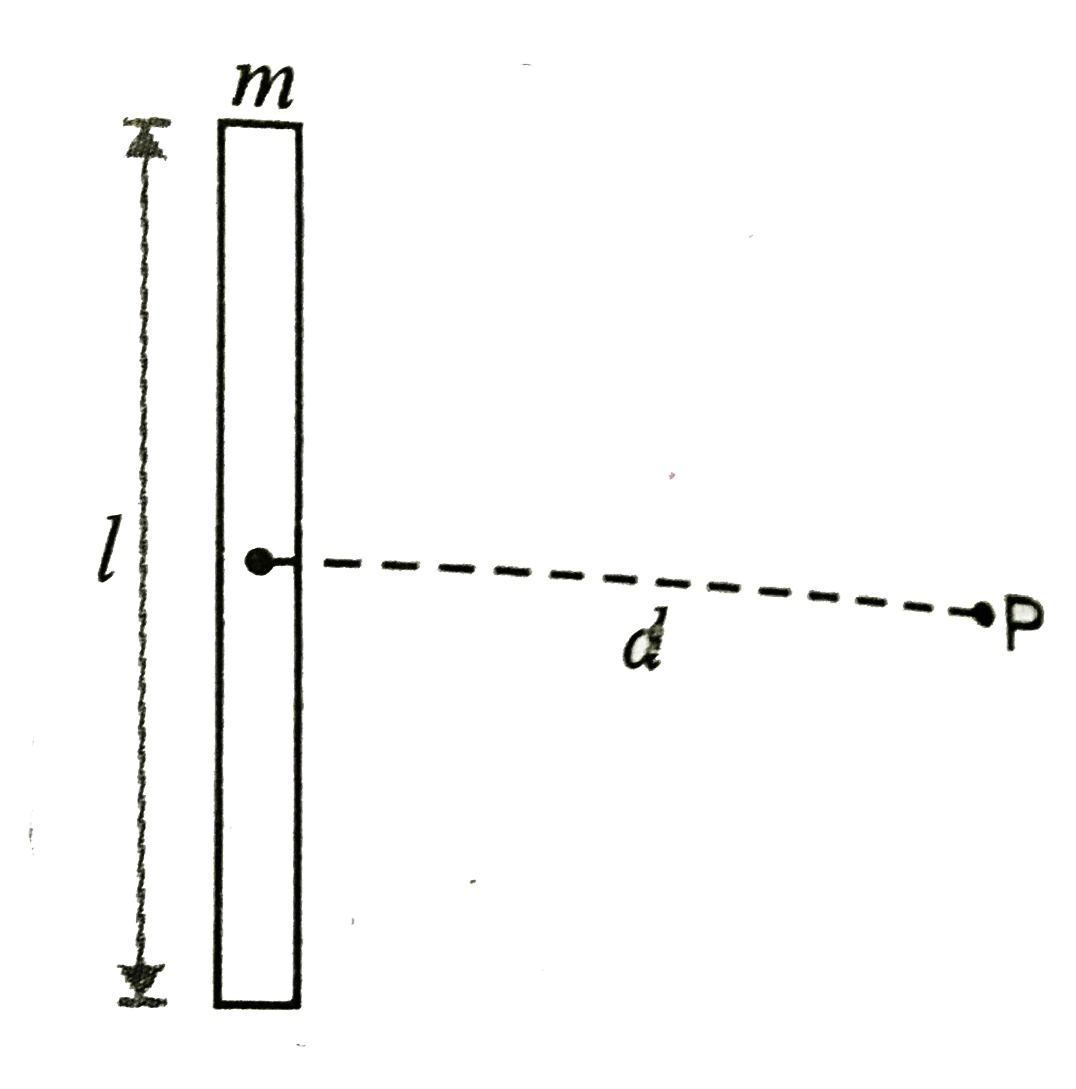 A4Gmd√4d2+l2B2Gmd√l2+4d2C2√2Gmd√l2+4d2Dnone of the above
A4Gmd√4d2+l2B2Gmd√l2+4d2C2√2Gmd√l2+4d2Dnone of the above
Calculate gravitational field intensity at a distance x on the axis from centre of a uniform disc of mass M and radius R .
View SolutionFind the intensity of gravitational field at a point lying at a distance x from the centre on the axis of a ring of radius a and mass M.
View SolutionFind the gravitational potential energy of a system consisting of a uniform rod AB of mass M, length l and a point mass m as shown in figure.
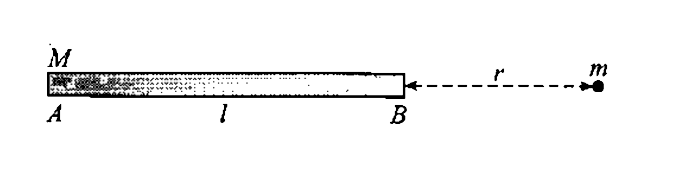
View Solution" The force of attraction on a particle of mass "m" placed at the centre of curvature of a semicircular wire of length L and mass "M" is "
View SolutionThe ratio of the magnetic field at the centre of a current carrying circular wire and the magnetic field at the centre of a semi-circular coil made from the same length of wire will be
View Solution
