A cosmic body A moves to the sun with velocity v0(when far from the sun) and aiming parameter l, the arm of the vector v0, relative to the centre of the sun. find the minimum distance by which this body will get to the sun. mass of the sum is M.
GMv20⎡⎢⎣ ⎷1+(lv20GM)2−1⎤⎥⎦
GMv20−1
GMv20⎡⎢⎣ ⎷1+(lv20GM)2+1⎤⎥⎦
GMlv20−1
The correct Answer is:A
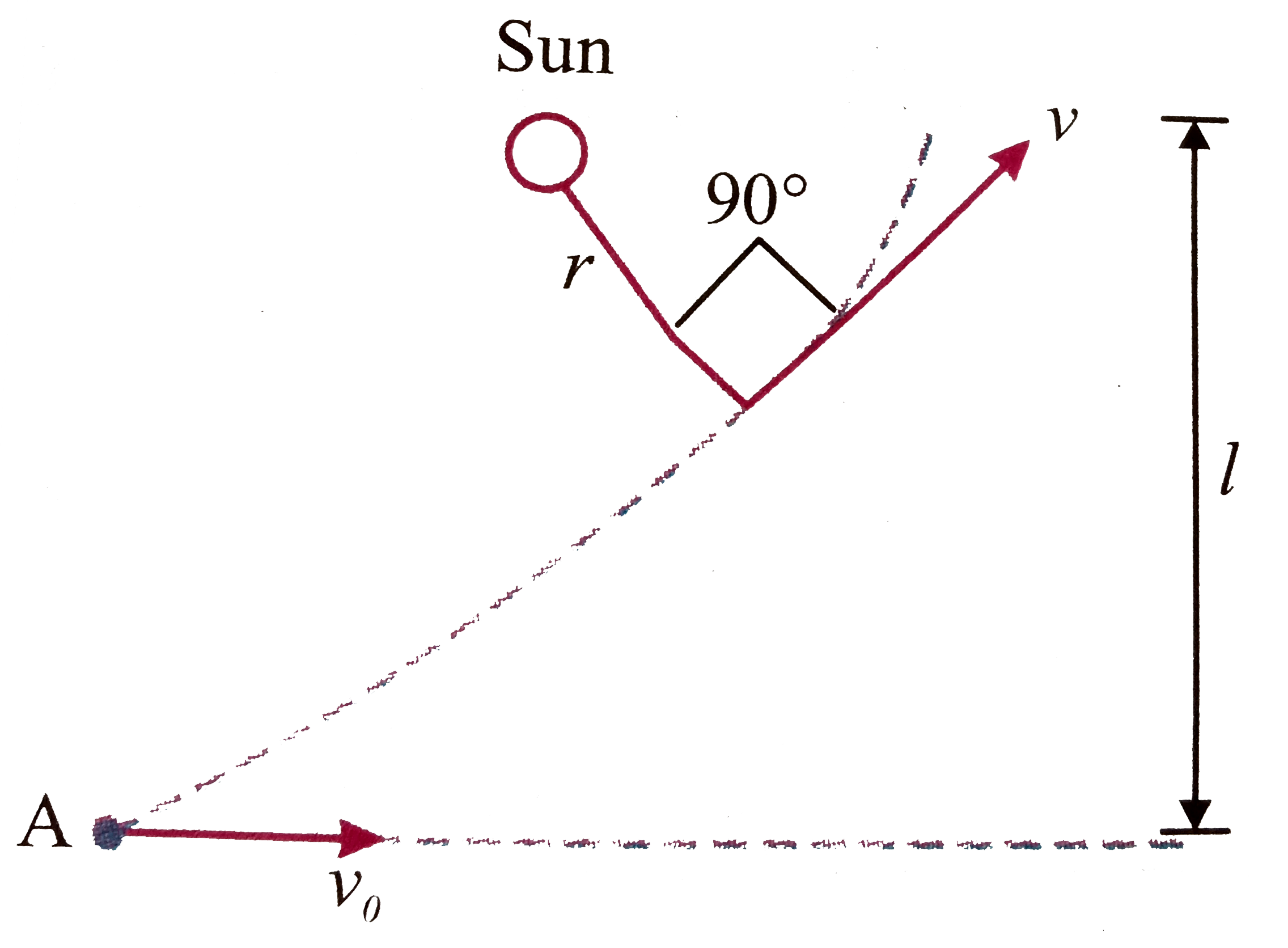
Let r be the minimum distance and m the mass of cosmic body A. applying conservation of angular momentum (about sun) and conservation of mechanical energy, we have,
mv0l=mvr......(1)
12mv20=12mv2−GMmr.....(2)
Solving these two equation, we have
r=GMv20⎡⎢⎣
⎷1+(lv20GM)2−1⎤⎥⎦
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - ILLUSTRATION49videos
GRAVITATION
- BOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - EVALUATE YOURSELF -13videos
GRAVITATION
- BOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - LEVEL-V54videos
GRAVITATION
- BOOK - NARAYNACHAPTER - FRICTIONEXERCISE - Passage type of questions I6videos
FRICTION
- BOOK - NARAYNACHAPTER - KINETIC THEORY OF GASESEXERCISE - LEVEL-III(C.W)52videos
KINETIC THEORY OF GASES
Similar Questions
A cosmic by A moves to the Sun with velocity v0 (when far from the Sun) and aiming parameter l the arm of the vector v0 relative to the centre of the Sun (figure). Find the minimum distance by which this body will get to the Sun.
 View Solution
View SolutionA planet of mass moves alng an ellipes around the sun so that its maximum distance from the sum are equal to r1 and r2 respectively . Find the angular momenture L of this planet relative to the centre of the sun.
[Hint :L Rember that at the maximum and minimum distance velocity is perpendicular to tthe position vectors of the planet . Apply the princples of conservation of angula r momenture and energy .]View Solution
Knowledge Check
- Question 1 - Select One
Block B moves to the right with a constant velocity v0. The velocity of body A relative to B is
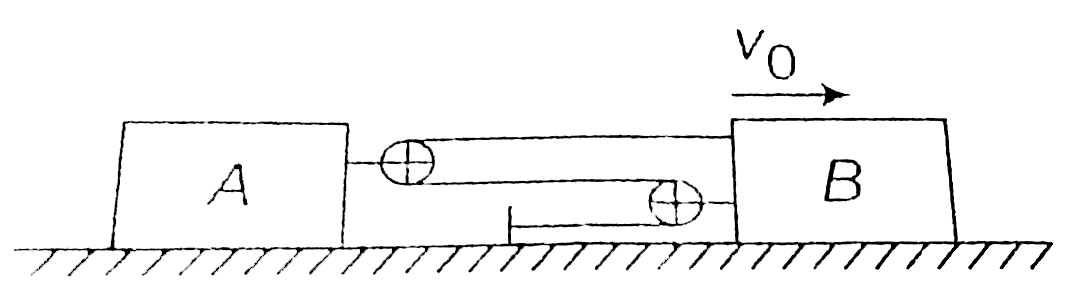 Av02, towards leftBv02, towards rightC3v02, towards leftD3v02, towards right
Av02, towards leftBv02, towards rightC3v02, towards leftD3v02, towards right - Question 2 - Select One
The earth revolves around the sun in an elliptical orbit. It has a speed v1 when it is at the minimum distance d1 from the sun. When it is at the maximum distance d2 from the sun, its speed is
Av1d2d1Bv1d1d2Cv21d2d1Dv1(d1d2)2 - Question 3 - Select One
A planet moves around the sun. At a given point P, it is closest from the sun at a distance d1 and has a speed v1. At another point Q, when it is farther from the sun at a distance d2, its speed will be
Ad21d22v1Bd2d1v1Cd22d21v1Dd1v1d2
A projectile is to be launched from the surface of the earth so as to escape the solar system. Consider the gravitational force on the projectile due to the earth and the sun nly. The projectile is projected perpendicular to the radius vector of the earth relative to the centre of the sun in the direction of motion of the earth. Find the minimum speed of projection relative to the earth so that the projectile escapes out of the solar system. Neglect rotation of the earth. mass if the sum Ms2×1030kg, Mass of the earth Me=6.4×1024kg Radius if the earthRe=6.4×106m, Earth- Sun distence r=1.5×1011m
View SolutionBlock B moves to the right with a constant velocity v0. The velocity of body A relative to B is :
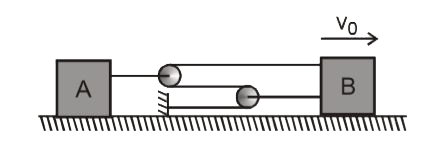 View Solution
View SolutionA planet A moves along an elliptical orbit around the Sun. At the moment when it was at the distance r0 from the Sun its velocity was equal to v0 and the angle between the radius vector r0 and the velocity vector v0 was equal to α. Find the maximum and minimum distances that will separate this planet from the Sun during its orbital motion.
View SolutionA planet moves around the sun. At a given point P, it is closest from the sun at a distance d1 and has a speed v1 At another point Q, when it is farthest from the sun at a distance d2 its speed will be
View SolutionA planet of mass m moves along an ellipse around the sun so that its maximum and minimum distance from the sun are equal to r1 and r2 respectively. Find the angular momentum of this planet relative to the centre of the sun. mass of the sun is M.
View Solution

