The density of the core a planet is ρ1 and that of the outer shell is ρ2. The radii of the core and that of the planet are R and 2R respectively. The acceleration due to gravity at the surface of the planet is same as at a depth R. Find the ratio of ρ1ρ2

37
94
73
38
The correct Answer is:C
Let m1 be the mass of the core and m2 be the mass of outer shell.
gA=gB (given) Then Gm1R2=G(m1+m2)(2R)2
∴4m1=(m1+m2) or
4{43πR2ρ1}=43πR3ρ1+{43π(2R)3−43πR3ρ2
∴4ρ1=ρ1+7ρ2⇒ρ1ρ2=73
Topper's Solved these Questions
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:ILLUSTRATION
Explore 49 Videos
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:EVALUATE YOURSELF -1
Explore 3 Videos
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:LEVEL-V
Explore 54 Videos
- FRICTIONBook:NARAYNAChapter:FRICTIONExercise:Passage type of questions I
Explore 6 Videos
- KINETIC THEORY OF GASESBook:NARAYNAChapter:KINETIC THEORY OF GASESExercise:LEVEL-III(C.W)
Explore 52 Videos
Similar Questions
The density of the core of planet is ρ1 and that of the outer shell is ρ2. The radius of the core that of the planet are R and 2R respectively. Gravitastional intensity at the surface of the planet is same as at a depth R. Find the ratio ρ1ρ2 , assuming them to be uniform independently.
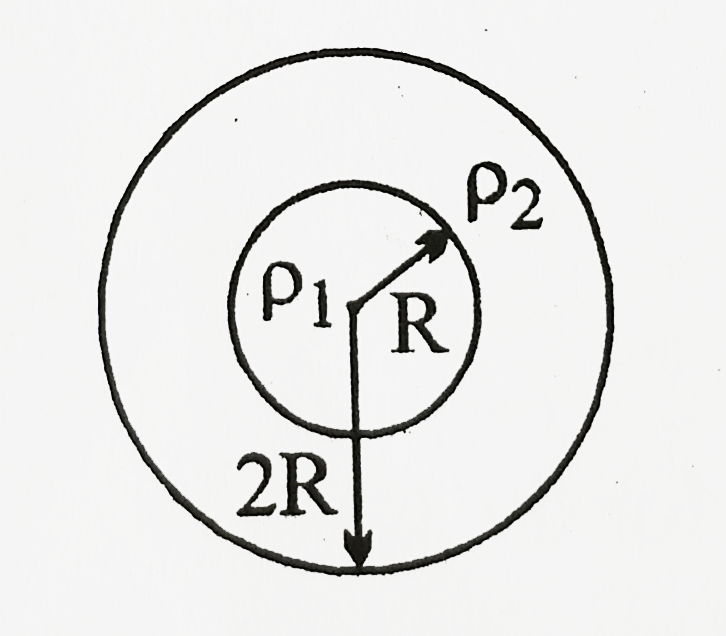
View SolutionThe density of the core of a planet is x and that of outer shell is y. The radii of the core and that of the planet are R and 2R. The acceleration due to gravity at the surface of planet is same as at a depth R. The ratio of x and y is n/3. Find the value of n.
View Solution
Knowledge Check
The acceleration due to gravity near the surface of a planet of radius R and density d is proportional to
AρRBρR−1Cρ−1R−2DρR2Suppose there are two planets, 1 and 2, having the same density but their radii are R1andR2 respectively, where R1>R2. The accelerations due to gravity on the surface of these planets are related as
Ag1>g2Bg1<g2Cg1=g2DCan't say anythingIf different planets have the same density but diferent radii then the acceleration due to gravity (g) on the surface of the planet will depend on its radius (R) as
Ag∝1R2Bg∝1RCg∝RDg∝R2
A planet is made of two materials of density ρ1 and ρ2 as shown in figure. The acceleration due to gravity at surface of planet is same as a depth 'R'. The ratio of ρ1ρ2 is x3. Find the value of x.

View SolutionA planet has a core of density ρ1 and the density of the outer shell is ρ2. R and 3R are the radii of the core and the planet respectively. Also, it is given that gravitational acceleration at the surface of the planet is equal to that at the surface of core. Hence, compute the ratio e ratio ρ1ρ2.
View SolutionTwo planets of radii r1 and r2 are made from the same material. The ratio of the acceleration of gravity g1/g2 at the surfaces of the planets is
View SolutionThe radii of two planets are R and 2R respectively and their densities p and p/4 respectively. What is the ratio of acceleration due to gravity at their surfaces?
View SolutionThe radii of two planets are R and 2R, respectively, and their densities are ρ and ρ2, respectively. The ratio of acceleration due to gravity at their surfaces is ah. Find (a+b).
View Solution